Miary autokorelacji danych poligonowych

Author

Anna Dmowska, Jakub Nowosad

1 Autokorelacja przestrzenna danych poligonowych

Autokorelacja przestrzenna (spatial autocorrelation) określa pewną zależność, która może być obserowana jako zgrupowania (klastry) podobnych wartości lub systematyczny wzorzec przestrzenny (spatial pattern).

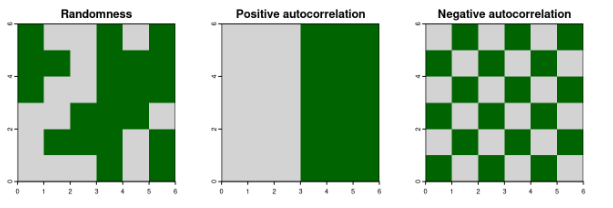
Losowość przestrzenna	Dodatnia autokorelacja przestrzenna	Ujemna autokorelacja przestrzenna
wartości obserwowane w danym obszarze nie zależą od wartości obserwowanych w sąsiednich obszarach	obserwuje się podobne wartości w sąsiadujących obszarach (wysokie wartości otoczone wysokimi, lub niskie niskimi)	wartości sąsiednie różnią się od siebie (np. niskie wartości otoczone wysokimi)

1.1 Miary autokorelacji przestrzennej

wykorzystywane do testowania istnienia autokorelacji przestrzennej
Miary globalne
- jednoliczbowy wskaźnik autokorelacji przestrzennej lub ogólnego podobieństwa regionów
- informuje o tym, że wartości nie są w przestrzeni rozmieszczone losowo -> tj. istnieją przesłanki, że podobne wartości grupują się w przestrzeni
- miary globalne nie informują nas gdzie zlokalizowane są zgrupowania podobnych wartości
- statystyki globalne: I Morana, C Geary’ego, G Getisa & Orda
Miary lokalne
- obliczane dla każdego regionu;
- pozwalaja odpowiedzieć na pytanie: czy dany region jest otoczony regionami o wysokich lub niskich wartościach? czy dany region jest podobny/różny wzgledem regionow sąsiednich?
- statystyki lokalne: Lokalne I Morana, Lokalne C Geary’ego, Lokalne G Getisa & Orda

1.2 Miary autokorelacji przestrzennej

Statystyka przestrzenna	Interpretacja	Komenda w R
	MIARY GLOBALNE
Moran $I$	$I > 0$ - dodatnia autokorelacja przestrzenna $I < 0$ - ujemna autokorelacja przestrzenna $I = 0$ - brak autokorelacji	moran() moran.test() moran.mc() moran.plot()
Geary $C$	$0-1$ - dodatnia autokorelacja przestrzenna $1-2$ - ujemna autokorelacja przestrzenna $1$ - brak autokorelacji	geary() geary.test() geary.mc()
Getis & Ord $G$	testuje $H_0$ o braku autokorelacji przestrzennej przeciwko $H_A$ o dodatniej autokorelacji przestrzennej. Nie mierzy ujemnej autokorelacji przestrzennej.	globalG.test()
	MIARY LOKALNE
Local Moran $I_{i}$	$I_{i} > 0$ - grupowanie podobnych wartości (wyższych lub niższych od średniej) $I_{i} < 0$ - połączenie różnych wartości (np. wysokie wartości otoczone niskimi wartościami lub niskie wartości otoczone wysokimi wartościami)	local.moran()
Local Geary $C_{i}$	$C_i < 0$ - niskie wartości wskazują na dodatnią autokorelację przestrzenną (podobieństwo regionu $i$ z sąsiadami) $C_i > 0$ - wysokie wartości wskazują na ujemną autokorelację przestrzenną, tj. region nie jest podobny do sąsiadów $C_i = 0$ - brak autokorelacji przestrzennej	localC(), localC_perm()
Local $G_{i}$	$G_{i} > 0$ - zgrupowanie regionów o relatywnie wysokich wartościach, klaster wysokich wartości (hot-spots) $G_{i} < 0$ - zgrupowanie regionów o relatywnie niskich wartościach, klaster niskich wartości (cold-spots)	localG(), localG_perm()

Źródło: Kopaczewska K. 2023. Przestrzenne metody ilościowe w R. (rozdział 4, str. 264-265), uzupełnione

2 Miary autokorelacji przestrzennej w R

Obliczenie miar autokorelacji przestrzennej w R wymaga wykonania dwóch kroków:

Utworzenie macierzy wag przestrzennych na podstawie wybranego sąsiedztwa i standaryzacji.
Obliczenie globalnych i lokalnych statystyk autokorelacji przestrzennych.

2.1 Pakiet `spdep`

Pakiet spdep dostarcza funkcji pozwalających na:

tworzenie macierzy przestrzennych (poly2nb, nb2listw)
obliczanie miar autokorelacji przestrzennych (patrz tabela powyżej)

3 Przykład: Stopa bezrobocia w Polsce w 2023 roku

library(sf)
library(tmap)
library(spdep)
library(dplyr)

3.1 Dane

W przykładzie zostaną wykorzystane dane dotyczące stopy bezrobocia w powiatach w Polsce w 2023 roku. Dane zostały pobrane z Banku Danych Lokalnych.

Plik bezrobocie_pl.csv zawiera identyfikator powiatu, nazwę powiatu oraz dane dotyczące stopy bezrobocia dla lat 2004, 2010, 2021, 2023 (odpowiednio SB2004, SB2010, SB2021, SB2023).
Plik powiaty_pl.gpkg zawiera granice powiatów w Polsce.
Plik wojewodztwa.gpkg zawiera granice województw, jest używany wyłącznie przy wizualizacji wyników.

bezrobocie = read.csv("data/bezrobocie_pl.csv", sep = ";", dec = ".")
powiaty_granica = read_sf("data/powiaty_pl.gpkg")
woj_granica = read_sf("data/wojewodztwa.gpkg")

Aby połączyć dane przestrzenne z informacją o stopie bezrobocia wykorzystane zostaną pola TERYT oraz Kod. Kolumna TERYT w pliku powiaty_pl.gpkg zawiera identyfikator powiatu w postaci 4 cyfr. Do pola TERYT trzeba dodać “000”, aby identyfikator powiatu w obu obiektach był taki sam. Do połączenia danych przestrzennych i nieprzestrzennych zostanie wykorzystana funkcja merge().

powiaty_granica$TERYT = as.integer(paste(powiaty_granica$TERYT, "000", sep=""))
powiaty = merge(powiaty_granica[, "TERYT"], bezrobocie, by.x = "TERYT", by.y = "Kod")

Wizualizacja została wykonana z wykorzystaniem pakietu tmap.

tm_shape(powiaty) + 
  tm_polygons("SB2023", palette = "YlOrBr") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)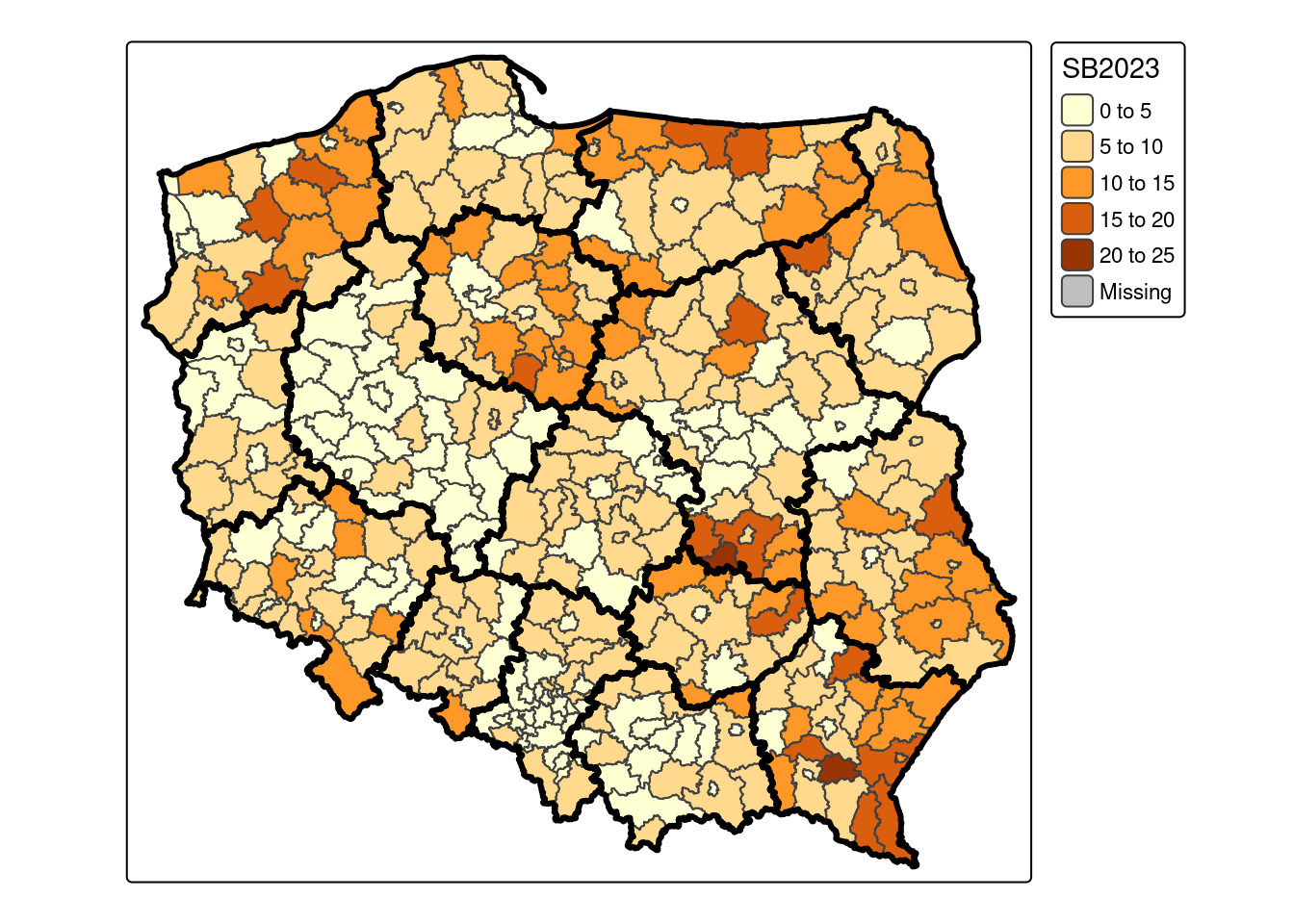

3.2 Cel analizy

analiza podobieństwa i różnic między obszarami/regionami
wyszukanie obszarów podobnych do siebie
znalezienie obszarów znacząco różnych od sąsiednich

3.3 Określanie sąsiedztwa danych poligonowych

Obliczenie miar autokorelacji przestrzennej wymaga określenia, które powiaty ze sobą sąsiadują oraz zapisania tej informacji w postaci macierzy wag przestrzennych.

3.3.1 Utworzenie macierzy wag przestrzennych

Macierz sąsiedztwa została utworzona z wykorzystaniem kryterium wspólnej granicy stosując regułę Queen.

Funkcja poly2nb() z pakieru spdep tworzy listę sąsiadów na podstawie regionów mających wspólne granice. Funkcja poly2nb() wymaga podania obiektu przestrzennego z granicami poligonów (w przykładzie obiekt powiaty) oraz określenia, czy stosowana będzie reguła queen (queen = TRUE), czy rook do określenia sąsiedztwa.
Funkcja nb2listw() z pakietu spdep tworzy macierz wag przestrzennych na podstawie macierzy sąsiedztwa. Funkcja nb2listw() wymaga podania obiektu zawierającego listę sąsiadów (obiekt będący wynikiem działania funkcji poly2nb() oraz typu macierzy wag (w przykładzie style = “W” oznacza, że zostanie utworzona macierz standaryzowana wierszami).

#macierz sasiedztwa
nb_q = poly2nb(powiaty, queen = TRUE)
#macierz wag przestrzennych. 
lw = nb2listw(nb_q, style = "W")
lw

Characteristics of weights list object:
Neighbour list object:
Number of regions: 380 
Number of nonzero links: 2006 
Percentage nonzero weights: 1.389197 
Average number of links: 5.278947 

Weights style: W 
Weights constants summary:
    n     nn  S0       S1      S2
W 380 144400 380 169.7589 1632.39

Na czym polega reguła QUEEN stosowana do określenia sąsiadów?

3.4 Globalne miary autokorelacji przestrzennej

3.4.1 Globalny test I Morana

Statystyka globalna I Morana jest najstarszą miarą przestrzenną wprowadzoną przez Morana w 1950 roku. Wykorzystywana jest do testowania globalnej autokorelacji przestrzennej:

$H_0$ : brak autokorelacji przestrzennej
$H_1$ : autokorelacja przestrzenna

Statystyka I Morana przyjmuje wartości:

$I = 0$ - wartości obserwacji w odległości $d$ są rozłożone losowo
$I > 0$ - autokorelacja dodatnia (pozytywna); sąsiadujące wartości są podobne; wartości podobne stykają się częściej niż losowo
$I < 0$ - autokorelacja ujemna (negatywna); sąsiadujące wartości są różne

Uwaga!: nawet wysokie wartości statystyki nie świadczą, że jest ona istotna statystycznie, dlatego poza policzeniem wartości statytyki należy wykonać test określający jej istotność statystyczną. Testowania istnienia autokorelacji przestrzennej może być wykonane wykorzystując dwa rodzaje testów:

tradycyjne podejście (moran.test())
symulację z wykorzystaniem Monte Carlo (moran.mc())

W tradycyjnym podejściu do testowania należy podać nazwę zmiennej (w przykładzie powiaty$SB2023) oraz macierz wag przestrzennych (argument listw). Do obliczenia statystyki I Morana zaleca się stosowanie macierzy wag przestrzennych standaryzowanej wierszami.

moran.test(powiaty$SB2023, listw = lw)


    Moran I test under randomisation

data:  powiaty$SB2023  
weights: lw    

Moran I statistic standard deviate = 12.997, p-value < 2.2e-16
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
      0.439401477      -0.002638522       0.001156697

W wyniku otrzymamy wartość statystyki Morana (Moran I statistics) oraz istotność statystyczną wyniku (p-value).

Stosowanie tradycyjnego podeścia do testowania istotności autokorelacji wymaga spełnienia wielu założeń. Dlatego częściej stosuje się podejście oparte o symulacji. W każdej symulacji wartości danych przypisano losowo do poligonów, wyliczana jest wartość statystyki, a następnie sprawdza się, czy obliczona wartość statystyki Morana na podstawie danych jest wśród wartości, których spodziewalibysmy się z losowego rozkładu.

Do wykonania testu z wykorzystaniem symulacji stosuje się funkcję moran.mc() z pakietu spdep. Funkcja ta wymaga podania nazwy zmiennej (w przykładzie powiaty$SB2023), macierzy wag przestrzennych (argument listw) oraz liczby symulacji (argument nsim).

moran_test = moran.mc(powiaty$SB2023, listw = lw, nsim = 99)
moran_test


    Monte-Carlo simulation of Moran I

data:  powiaty$SB2023 
weights: lw  
number of simulations + 1: 100 

statistic = 0.4394, observed rank = 100, p-value = 0.01
alternative hypothesis: greater

W wyniku otrzymamy wartość statystyki (statistic) oraz psedo p-value (p-value). Należy pamiętać, że w tym wypadku wartość pseudo p-value jest zależne od liczby symulacji. (gdybyśmy wykonali 999 symulacji, zamiast 99 pseudo p-value wyniesie 0.001). Niska wartość p-value nadal wskazuje na istotność statystyczną wyniku.

W przypadku stopy bezrobocia w powiatach wartość statystyki globalnej I Morana wyniosła 0,4394 co wskazuje na autokorelacja dodatnia (pozytywna), tj. istnieje przesłanka, że w danych istnieją zgrupowania powiatów o podobnych wartościach stopy bezrobocia.

3.4.2 Globalny test C Geary’ego

Miara C Geary’ego jest kolejną miarą globalną wykorzystywaną do testowania globalnej autokorelacji przestrzennej:

$H_0$ : brak autokorelacji przestrzennej
$H_1$ : autokorelacja przestrzenna

Statystyka C Geary’ego przyjmuje wartości w przedziale od 0 do 2.

0-1: autokorelacja dodatnia (pozytywna); sąsiadujące wartości są podobne
1: brak autokorelacji przestrzennej; sąsiadujące wartości są rozłożone losowo
1-2: autokorelacja ujemna (negatywna); sąsiadujące wartości nie są podobne

Tak jak w przypadku statystyki I Morana do testowania istotności można zastsować tradycyjne podejście (funkcja geary.test() z pakietu spdep) lub podejście oparte o symulacje (funkcja geary.mc() z pakietu spdep).

geary.test(powiaty$SB2023, listw = lw)


    Geary C test under randomisation

data:  powiaty$SB2023 
weights: lw   

Geary C statistic standard deviate = 11.024, p-value < 2.2e-16
alternative hypothesis: Expectation greater than statistic
sample estimates:
Geary C statistic       Expectation          Variance 
      0.541515148       1.000000000       0.001729799

geary.mc(powiaty$SB2023, listw = lw, nsim = 99)


    Monte-Carlo simulation of Geary C

data:  powiaty$SB2023 
weights: lw  
number of simulations + 1: 100 

statistic = 0.54152, observed rank = 1, p-value = 0.01
alternative hypothesis: greater

Wartość statystyki (0,54) wskazuje na istnienie autokorelacji dodatniej.

3.4.3 Globalny test G Getisa & Orda

Testuje hipotezę zerową o braku autokorelacji przestrzennej przeciwko hipotezie alternatywnej o dodatniej autokorelacji przestrzennej. Miara ta nie mierzy autokorelacji ujemnej.

$H_0$ : brak autokorelacji przestrzennej
$H_1$ : dodatnia autokorelacja przestrzenna

#obliczenie wag binarnych
lb = nb2listw(nb_q, style = "B")
#testowanie
globalG.test(powiaty$SB2023, listw = lb)


    Getis-Ord global G statistic

data:  powiaty$SB2023 
weights: lb   

standard deviate = 5.679, p-value = 6.774e-09
alternative hypothesis: greater
sample estimates:
Global G statistic        Expectation           Variance 
      1.582796e-02       1.392862e-02       1.118554e-07

Jak zinterpretujesz wynik?

3.5 Lokalne miary autokorelacji przestrzennej

3.5.1 Zależność między regionem a sąsiadami

	Wartości niskie w regionie $i$ (L)	Wartości wysokie w regionie $i$ (H)
Wartości wysokie w regionach sąsiednich (H)	Kwadrat LH (Q2) Ujemna autokorelacja przestrzenna	Kwadrat HH (Q1) Dodatnia autokorelacja przestrzenna
Wartości niskie w regionach sąsiednich (L)	Kwadrat LL (Q3) Dodatnia autokorelacja przestrzenna	Kwadrat HL (Q4) Ujemna autokorelacja przetrzenna

3.5.2 Wykres rozrzutu Morana

Wykres rozrzutu Morana pokazuje zależność między wartościami zmiennej (oś x) oraz wartościami zmiennej późnionej przestrzennie (oś y, spatial lag, tj. średnia wartość wyliczona na podstawie sąsiadów graniczących z regionem). Pionowa przerywana linia wyznacza wartość średnią dla analizowanej zmiennej, pozioma przerywana linia oznacza średnią wartość dla zmiennej opóźnionej przestrzennie. Linie te dzielą wykres na 4 części.

moran.plot(powiaty$SB2023, listw = lw, labels = powiaty$Nazwa)
text(3, 15, "Q2: LH", cex = 2, col = "steelblue1")
text(22, 15, "Q1: HH", cex = 2, col = "red")
text(22, 2, "Q4: HL", cex = 2, col = "lightcoral")
text(3, 2, "Q3: LL", cex = 2, col = "blue")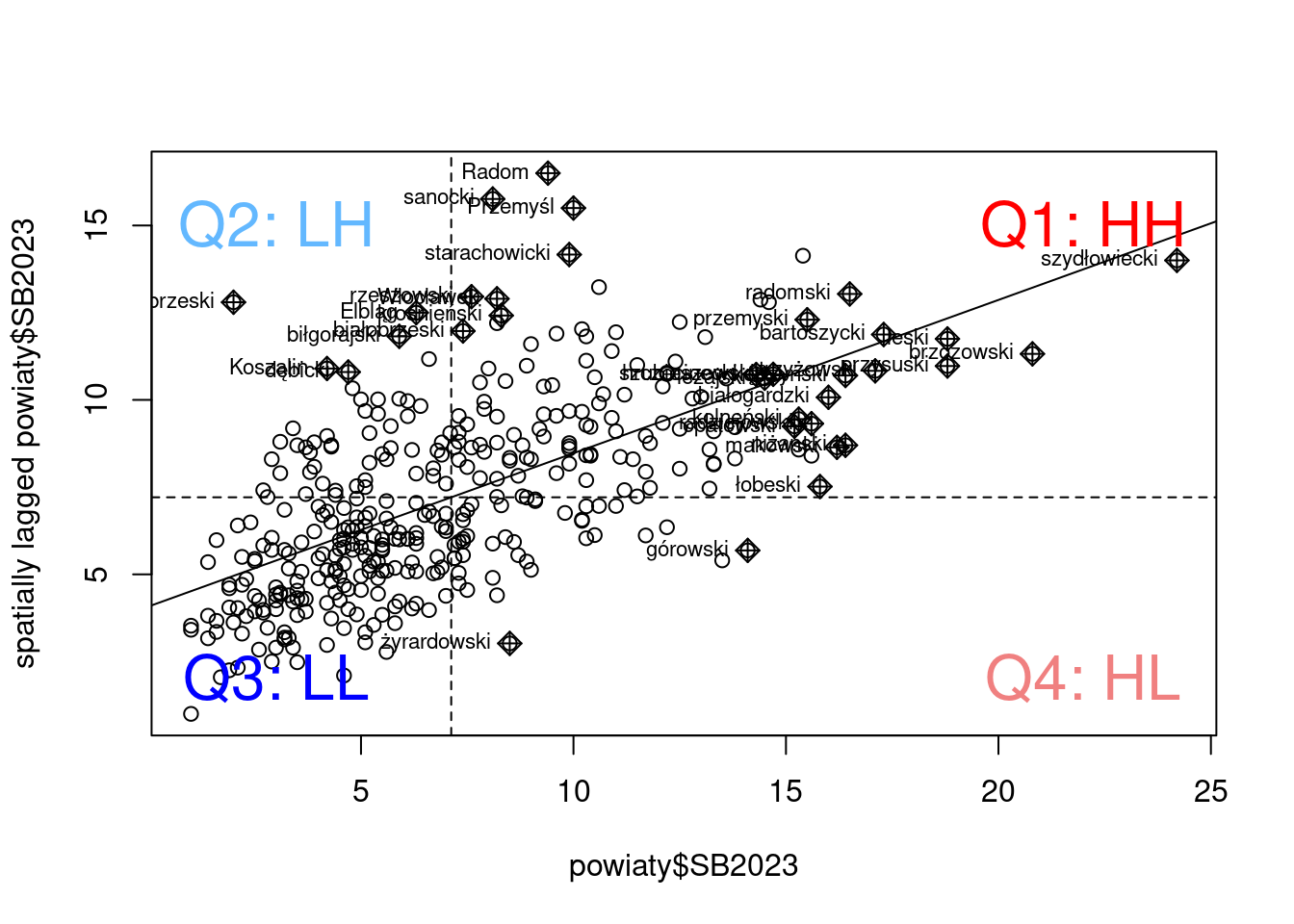

Kwarta 1 (Q1) wskazuje, że wartości relatywnie wysokie (wyższe od średniej) otoczone są przez relatywnie wysokie wartości sąsiadów, co wskazuje na istnienie autokorelacji dodatniej. Kwarta 3 (Q3) pokazuje, że wartości w regionie są niższe od średnich oraz są otoczone relatywnie niższymi wartościami sąsiadów (to też świadczy o autokorelacji dodatniej). Kwarta 2 (Q2) oraz kwarta 4 (Q4) przedstawiają ujemną autokorelacją przestrzenną. W przypadku kwarty 2 (Q2) relatywnie niskie wartości zmiennej (poniżej średniej) otoczone są przez relatywnie wysokie wartości dla sąsiadów. W kwarcie 4 relatywnie wysokie wartości w regionie (powyżej średniej) otoczone są przez relatywnie niskie wartości dla sąsiadów.

Wykres rozrzutu statystyki Morana można także wykonać dla wartości standaryzowanych. Wykres punktowy statystyki Morana wykonany w oparciu o standaryzowane wartości zmiennej oraz zmiennej opóźnionej przestrzennie (spatial lag) stanowi graficzną reprezentację globalnej Statystyki Morana. Nachylenie linii regresji jest tożsame z globalną statystyką Morana. Linie przerywane na wykresie wyznaczają średnią wartość obserwowanej zmiennej oraz średnią wartość zmiennej opóźnionej przestrzennie. Po standaryzacji średnie będą równe 0.

library(dplyr)
library(ggplot2)
#standaryzacja warości zmiennej
powiaty$SB_scaled = as.vector(scale(powiaty$SB2023))
#obliczenie wartości standaryzowanych dla zmiennej opóźnionej przestrzennie
powiaty$SB_scaled_lag = lag.listw(lw, powiaty$SB_scaled)

# typy zależnosci 
powiaty = powiaty |>
  mutate(mp_q = case_when(
    powiaty$SB_scaled >= 0 & powiaty$SB_scaled_lag >= 0 ~ "Q1: HH",
    powiaty$SB_scaled <= 0 & powiaty$SB_scaled_lag <= 0 ~ "Q3: LL",
    powiaty$SB_scaled >= 0 & powiaty$SB_scaled_lag <= 0  ~ "Q4: HL",
    powiaty$SB_scaled<= 0 & powiaty$SB_scaled_lag >= 0 ~ "Q2: LH"
  )) # classify the cluster types

#wykres rozrzutu
ggplot(powiaty, aes(x=SB_scaled, y=SB_scaled_lag)) + geom_point(aes(col = mp_q), shape=20, show.legend = F, size = 3) + 
    scale_color_manual(values = c("Q1: HH"= "red", "Q2: LH" = "steelblue1", "Q3: LL" = "blue", "Q4: HL" = "lightcoral")) + 
    geom_hline(yintercept=mean(powiaty$SB_scaled_lag), lty=2) + 
    geom_vline(xintercept=mean(powiaty$SB_scaled), lty=2) + theme_minimal(base_size = 18) + 
    geom_smooth(formula=y ~ x, method="lm") + 
    annotate(geom="text", x=-1, y=-1.5, label="Q3: LL", color="blue", size = 7) + 
    annotate(geom="text", x=-1, y=2, label="Q2: LH", color="steelblue1", size = 7) + 
    annotate(geom="text", x=3, y=-1.5, label="Q4: HL", color="lightcoral", size = 7) + 
    annotate(geom="text", x=3, y=2, label="Q1: HH", color="red", size = 7)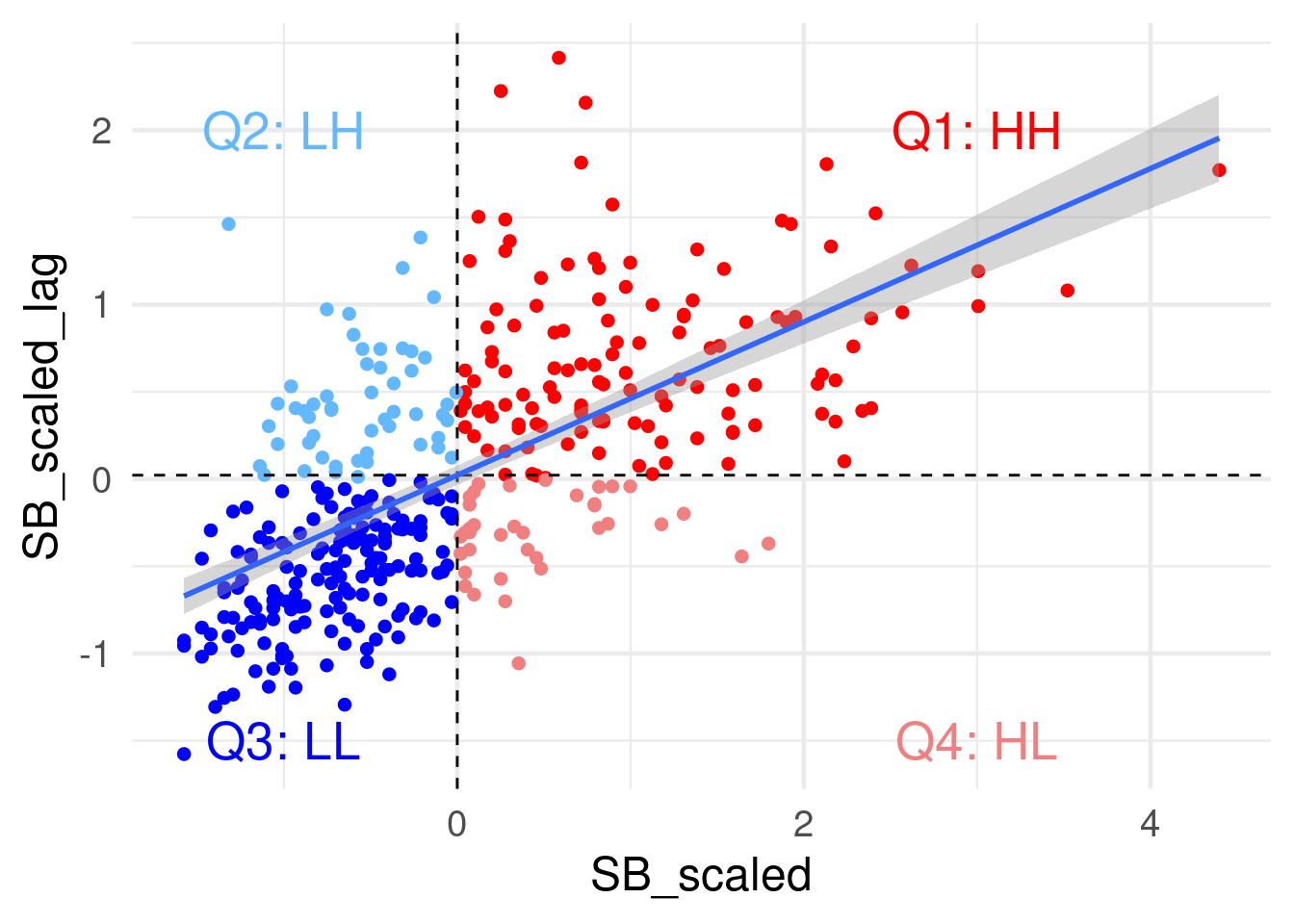

3.5.3 Lokalny test Morana $I_{i}$

Statytyka lokalna Morana $I$ obliczana jest dla każdego regionu. Statystyka ta mierzy czy region jest otoczony przez regiony sąsiedzkie o podobnych czy różnych wartościach w stosusnku do losowego rozmieszczenia tych wartości w przestrzeni:

$I_{i} > 0$ - grupowanie podobnych wartości (wyższych lub niższych od średniej)
$I_{i} < 0$ - połączenie różnych wartości (np. wysokie wartości otoczone niskimi wartościami lub niskie wartości otoczone wysokimi wartościami)

Statytyka lokalna Morana $I$umożliwia wykrycie znaczących grup identycznych wartości wokół określonej lokalizacji (klastrów).

W R do obliczenia lokalnej statystyki Morana wykorzystuje się funkcję localmoran() z pakietu spdep. Funkcja ta wymaga zdefiniowania wartości zmiennej oraz macierzy wag przestrzennych (argument listw).

locm = localmoran(powiaty$SB2023, listw = lw)
head(locm)

           Ii          E.Ii      Var.Ii        Z.Ii Pr(z != E(Ii))
1 -0.02618885 -3.278138e-03 0.174557285 -0.05483648      0.9562687
2 -0.14316746 -4.621114e-04 0.028866576 -0.83992908      0.4009482
3  0.01752931 -6.811164e-05 0.004256387  0.26972955      0.7873683
4 -0.66667478 -8.537739e-03 0.452226259 -0.97867488      0.3277406
5  0.19350355 -1.352469e-03 0.072156657  0.72539678      0.4682086
6  0.11137371 -3.325013e-04 0.024994379  0.70657154      0.4798328

W wyniku otrzymamy wartość statystyki Morana dla każdego regionu (Ii) oraz wartość poziomu istotności statystyki wyliczonej dla każdego regionu (kolumna Pr(z != E(Ii))). Wartości poziomu istotności oraz statystyki możemy przypisać do obiektu powiaty co pozwoli nam na zwizualizowanie wyników.

powiaty$I = locm[, 1]
powiaty$I_pvalue = locm[, 5]

Poniższa mapa przedstawia rozkład wartości statystyki lokalnej I Morana, bez uwzględniania informacji o istotności statystycznej wyniku. Kolorem niebieskim zaznaczono powiaty dla których odnotowano wartości wskazujące na autokorelację ujemną, a kolorem czerwonym na autokorelację dodatnią.

tm_shape(powiaty) + 
  tm_polygons(fill = "I",  palette = "-RdBu", midpoint = 0)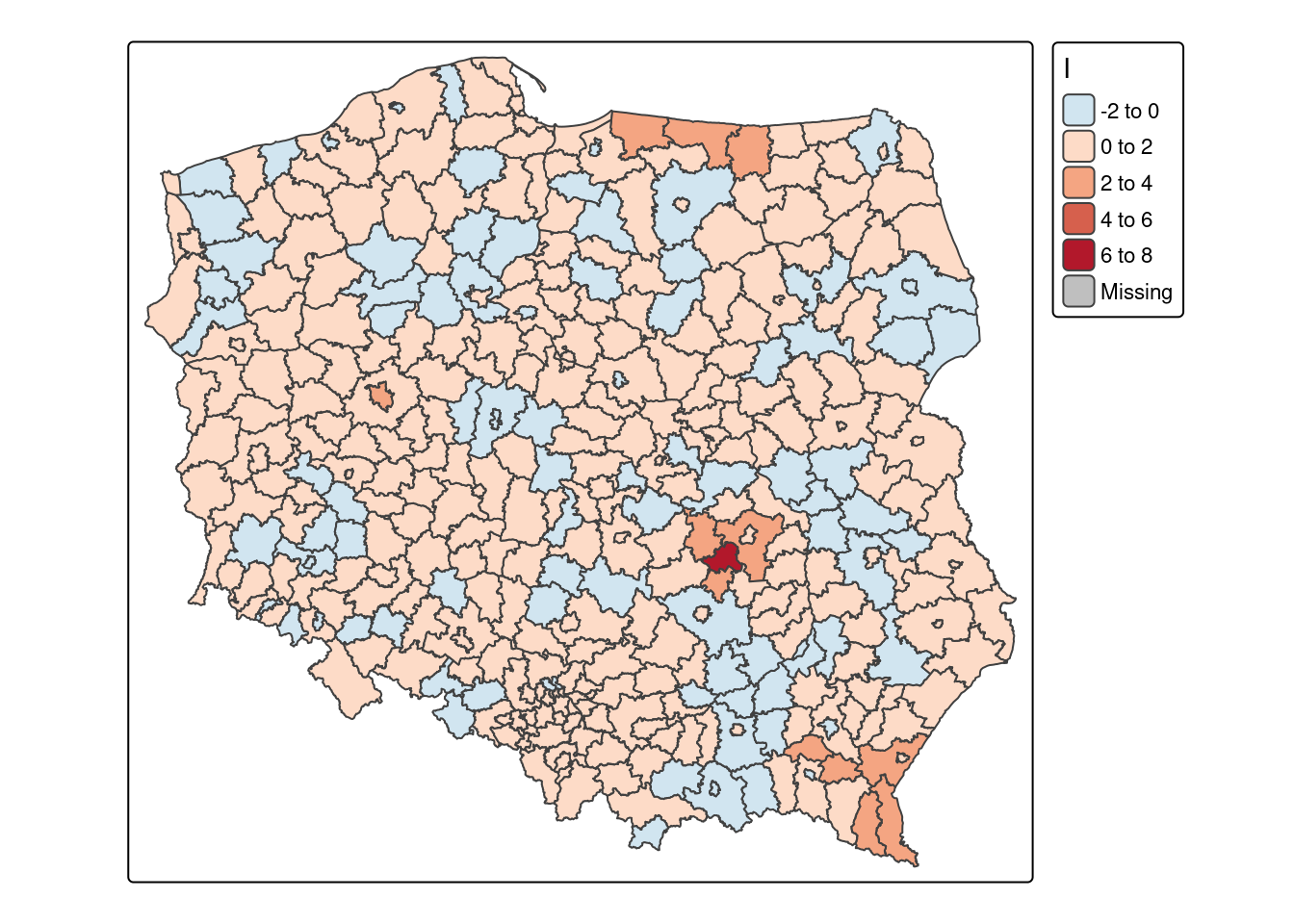

Na poniższej mapie kolorem zilustrowano wartości poziomu isotności wyliczonego dla każdego powiatu. Powiaty oznaczone kolorem szarym na mapie nie mają istotnych statystycznie wartości statystyki lokalnej I Morana.

tm_shape(powiaty) + tm_polygons(fill = "I_pvalue", breaks = c(0, 0.001, 0.01, 0.05, 1), palette = c("red", "orange", "yellow", "darkgrey"), colorNA = "white")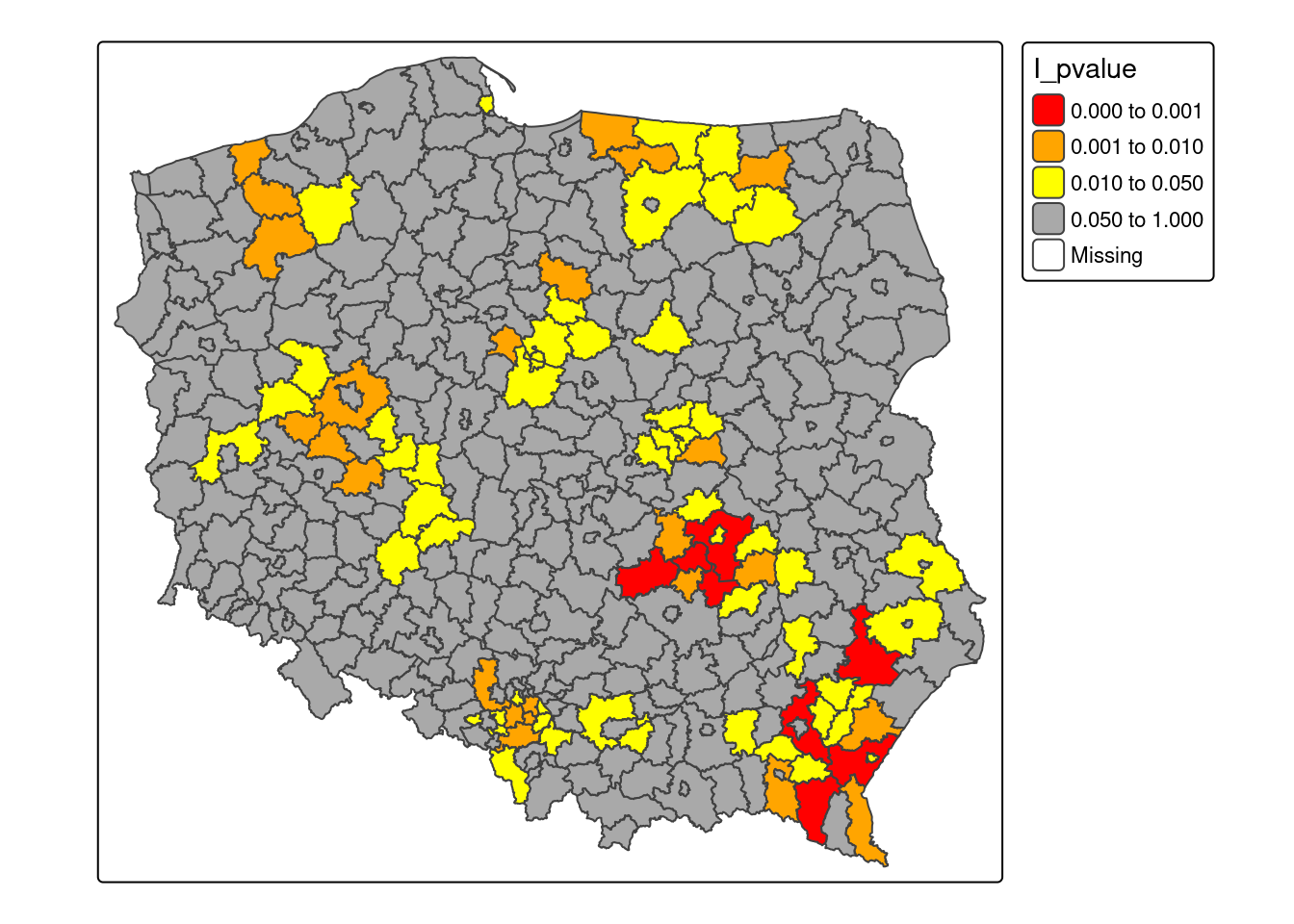

Statystyka lokalna I Morana umożliwia identyfikację klastrów wysokich lub niskich wartości. Do identyfikacji klastrów wykorzystuje się wyłącznie istotne statystycznie wartości statystyki I Morana. Powiaty zostaną sklasyfikowane na 4 grupy: - wysokie wartości otoczone wysokimi wartościami - niskie wartości otoczone niskimi wartościami - wysokie wartości otoczone niskimi wartościami - niskie wartości otoczone wysokimi wartościami.

Do podziału na 4 grupy wykorzystuje się wykres rozrzutu Morana.

#standaryzacja wartości zmiennej SB2023
powiaty$SB_scaled = as.vector(scale(powiaty$SB2023))
#obliczenie wartości standaryzowanych dla zmiennej opóźnionej przestrzennie
powiaty$SB_scaled_lag = lag.listw(lw, powiaty$SB_scaled)

#klasyfikacja na 4 grupy biorąc pod uwagę kwartę wykresu rozrzutu oraz informację czy statystyka jest istotna statystycznie
powiaty = powiaty |>
  mutate(mcluster_type = case_when(
    powiaty$SB_scaled >= 0 & powiaty$SB_scaled_lag >= 0 & locm[, 5] <= 0.05 ~ "High-High",
    powiaty$SB_scaled <= 0 & powiaty$SB_scaled_lag <= 0 & locm[, 5] <= 0.05 ~ "Low-Low",
    powiaty$SB_scaled >= 0 & powiaty$SB_scaled_lag <= 0 & locm[, 5] <= 0.05 ~ "High-Low",
    powiaty$SB_scaled<= 0 & powiaty$SB_scaled_lag >= 0 & locm[, 5] <= 0.05 ~ "Low-High",
    locm[, 5] > 0.05 ~ "Not Significant"
  )) # classify the cluster types


cluster_colors <- c("High-High"= "red", "High-Low" = "lightcoral", "Low-High" = "steelblue1", "Low-Low" = "blue", "Not Significant" = "lightgrey" )
MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$mcluster_type)]

tm_shape(powiaty) + 
  tm_polygons("mcluster_type", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)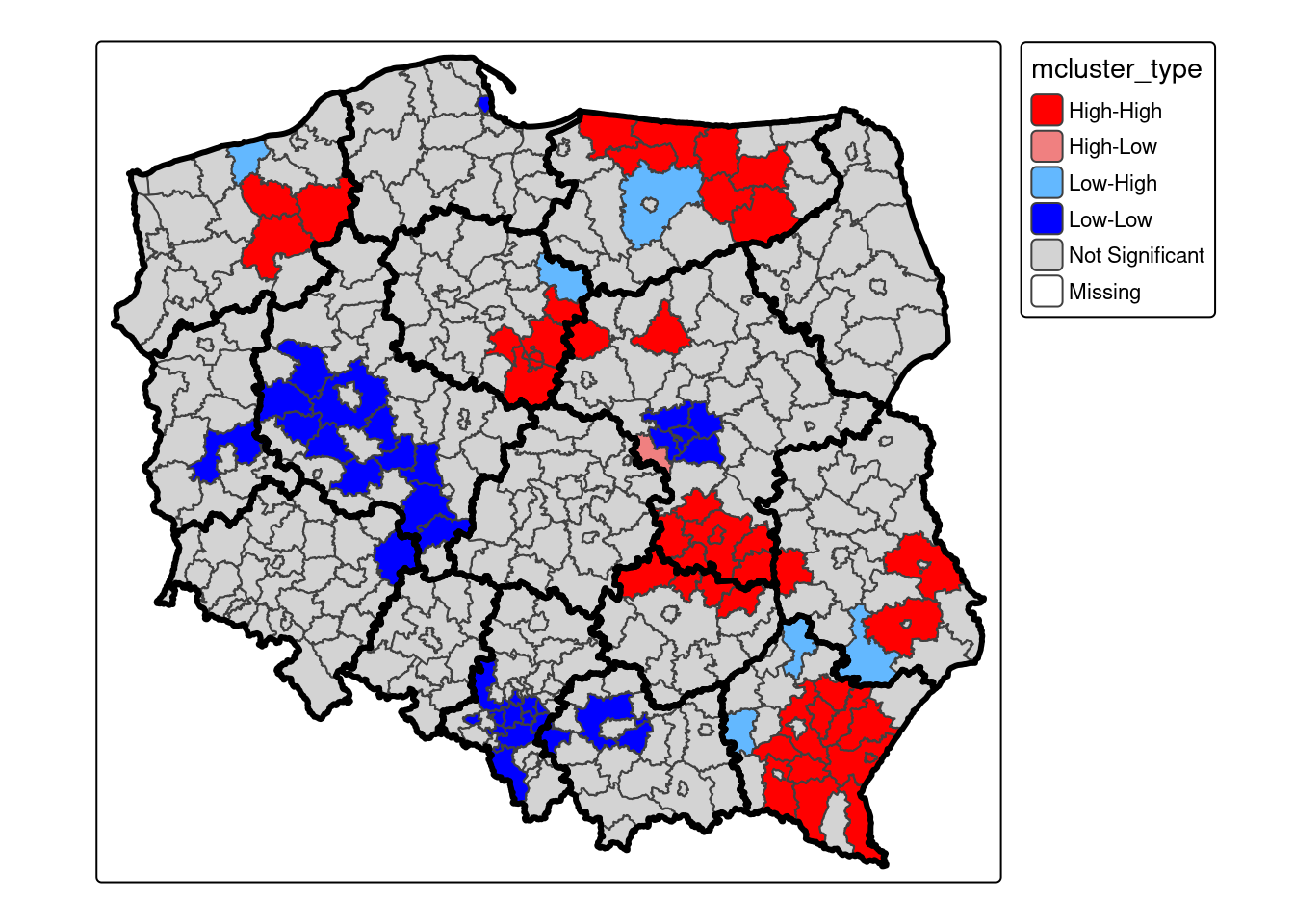

Powyższą klasyfikację można także uzyskać stosując funkcję hotspot() z pakietu spdep.

localmoran(powiaty$SB2023, listw = lw) |>  hotspot(Prname="Pr(z != E(Ii))", cutoff=0.05, p.adjust="none") -> powiaty$localI

table(powiaty$localI)


  Low-Low  High-Low  Low-High High-High 
       33         1         6        43

cluster_colors <- c("High-High"= "red", "High-Low" = "lightcoral", "Low-High" = "steelblue1", "Low-Low" = "blue")
MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$localI)]

tm_shape(powiaty) + 
  tm_polygons("localI", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)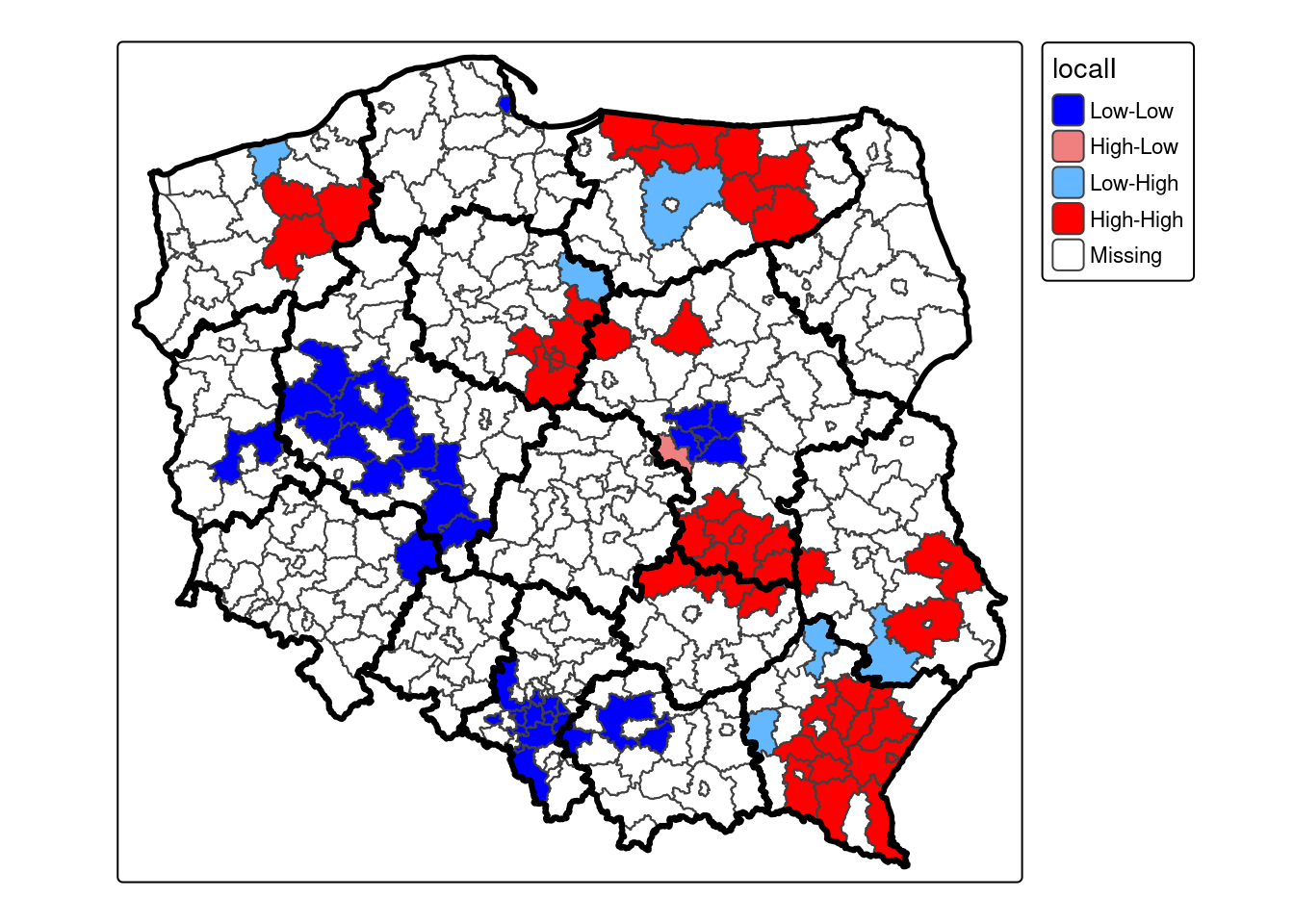

3.5.4 Lokalna statystyka C Geary’ego

Lokalna statystyka C Geary’ego pokazuje średnie różnice między obiektem a sąsiadami co pomaga znależć wartośc odstające. Niskie wartości lokalnego Geary’ego wskazują na dodatnią autokorelację przestrzenną, a duże na ujemną autokorelację przestrzenną.

0: brak autokorelacji
$C_{i} < 0$ - niskie wartości wskazują na dodatnią autokorelację przestrzenną, tj. podobieństwo regionu $i$ z sąsiednimi
$C_{i} > 0$ - wysokie wartości wskazują na ujemną autokorelację przestrzenną, tj. region nie ma podobnych wartości do sąsiadów

W R lokalną statystykę C Geary’ego oblicza się używając funkcji localC_perm() z pakietu spdep, który wymaga zdefiniowania zmiennej uwzględnianej w analizie oraz macierzy wag przestrzennych (argument listw). Funkcja hotspot() z pakietu spdep zwraca wektor z przypisanymi kategoriami klastrów dla określonego poziomu isotności. Kategorie te można przypisac do obiektu przestrzennego powiaty oraz zwizualizować.

localC_perm(powiaty$SB2023, listw = lw, nsim = 99) |>  hotspot(Prname="Pr(z != E(Ci)) Sim", cutoff=0.05, p.adjust="none") -> powiaty$localC

table(powiaty$localC)


     High-High        Low-Low Other Positive       Negative 
            29             50              2              3

cluster_colors <- c("High-High"= "red", "Low-Low" = "blue",  "Other Positive" = "lightcoral", "Negative" = "steelblue1", "Insignificant" = "lightgrey" )

MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$localC)]

tm_shape(powiaty) + 
  tm_polygons("localC", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)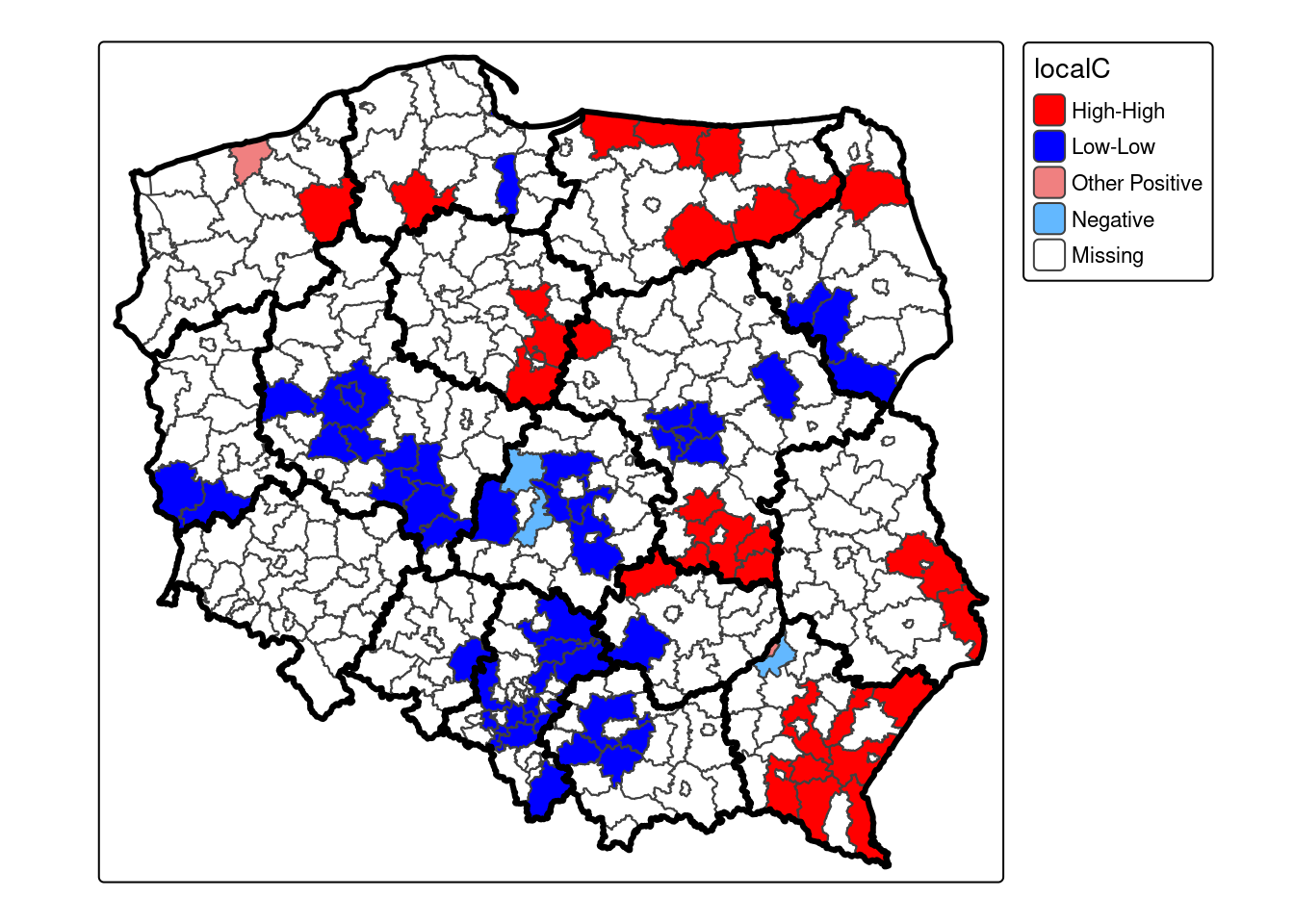

3.5.5 Lokalna statystyka G Getisa & Orda

Wskaźnik do identyfikacji lokalnych zależności przestrzennych (koncentracji przestrzennych), które nie pojawiają się w analizie globalnej:

$G_i > 0$ - zgrupowanie regionów o wysokich wartościach (region $i$ oraz regiony sąsiednie mają wysokie wartości) - tzw. klastr wysokich wartości (hot-spots)
$G_i < 0$ - zgrupowanie regionow o niskich wartościach (region $i$ jest otoczony przez podobne mu regiony o niskich wartościach) - tzw. cold-spots

Jako wysokie wartości uznaje się wartości wyższe od średniej, a jako niskie wartości uznaje się wartości niższe od średniej.

Lokalna statystyka G Getisa & Orda nie mierzy autokorelacji ujemnej.

W R lokalną statystykę G Getisa & Orda oblicza się używając funkcji localG_perm() z pakietu spdep, który wymaga zdefiniowania zmiennej uwzględnianej w analizie oraz macierzy wag przestrzennych (argument listw). Funkcja hotspot() z pakietu spdep zwraca wektor z przypisanymi kategoriami klastrów dla określonego poziomu isotności. Kategorie te można przypisac do obiektu przestrzennego powiaty oraz zwizualizować.

localG = localG_perm(powiaty$SB2023, listw = lw, nsim = 99)
localG |>  hotspot(Prname="Pr(z != E(Gi)) Sim", cutoff=0.05, p.adjust="none") -> powiaty$localG

table(powiaty$localG)


 Low High 
  46   29

cluster_colors <- c("Low" = "blue", "High"= "red")
MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$localG)]

tm_shape(powiaty) + 
  tm_polygons("localG", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)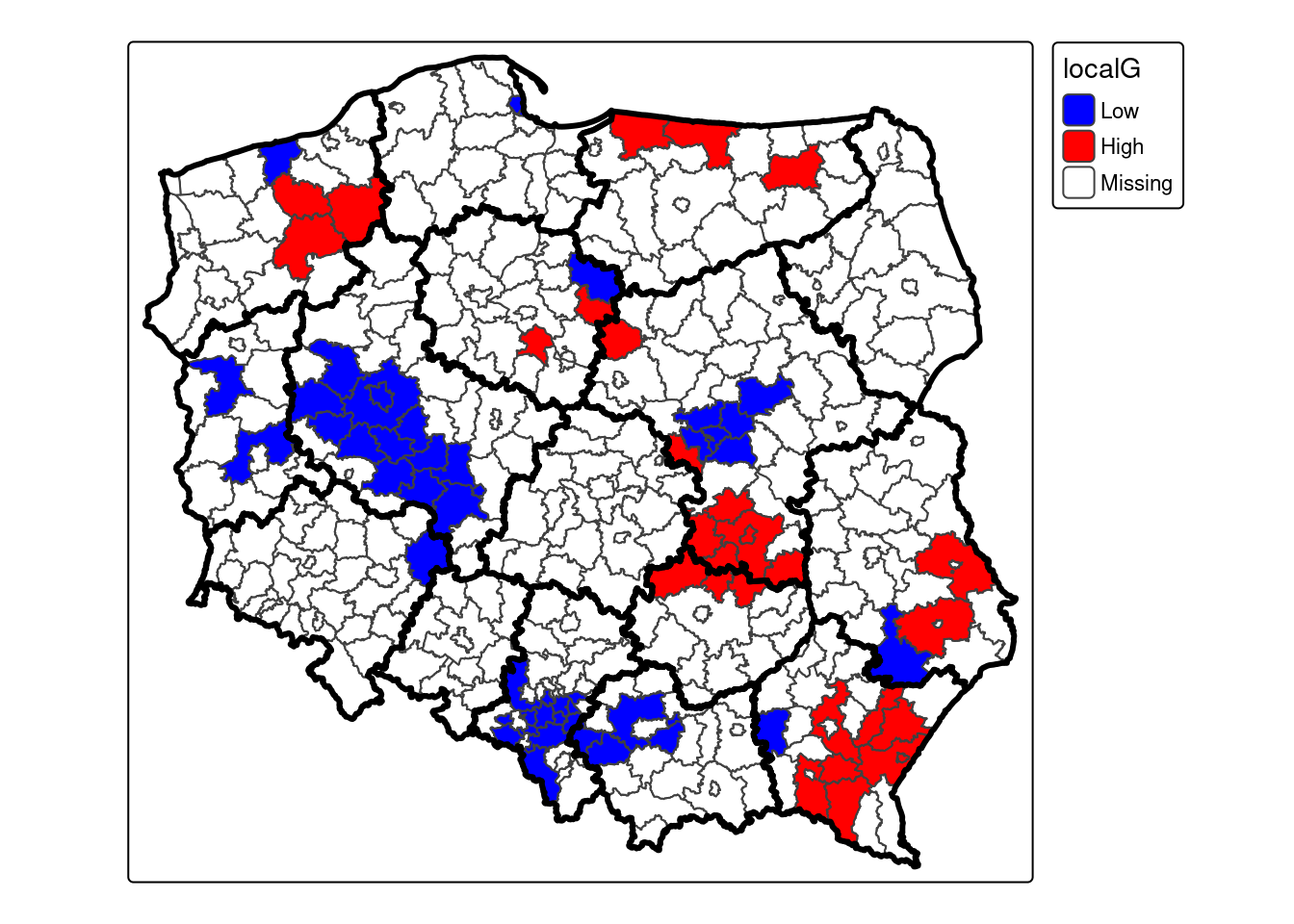

4 Przykład 2: Stopa bezrobocia w Polsce w 2004 roku

4.1 Dane

library(sf)
bezrobocie = read.csv("data/bezrobocie_pl.csv", sep = ";", dec = ".")
powiaty_granica = read_sf("data/powiaty_pl.gpkg")
woj_granica = read_sf("data/wojewodztwa.gpkg")

powiaty_granica$TERYT = as.integer(paste(powiaty_granica$TERYT, "000", sep=""))
powiaty = merge(powiaty_granica[, "TERYT"], bezrobocie, by.x = "TERYT", by.y = "Kod")

powiaty$SB2004[is.na(powiaty$SB2004)]<-0

tm_shape(powiaty) + 
  tm_polygons("SB2004", palette = "YlOrBr") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)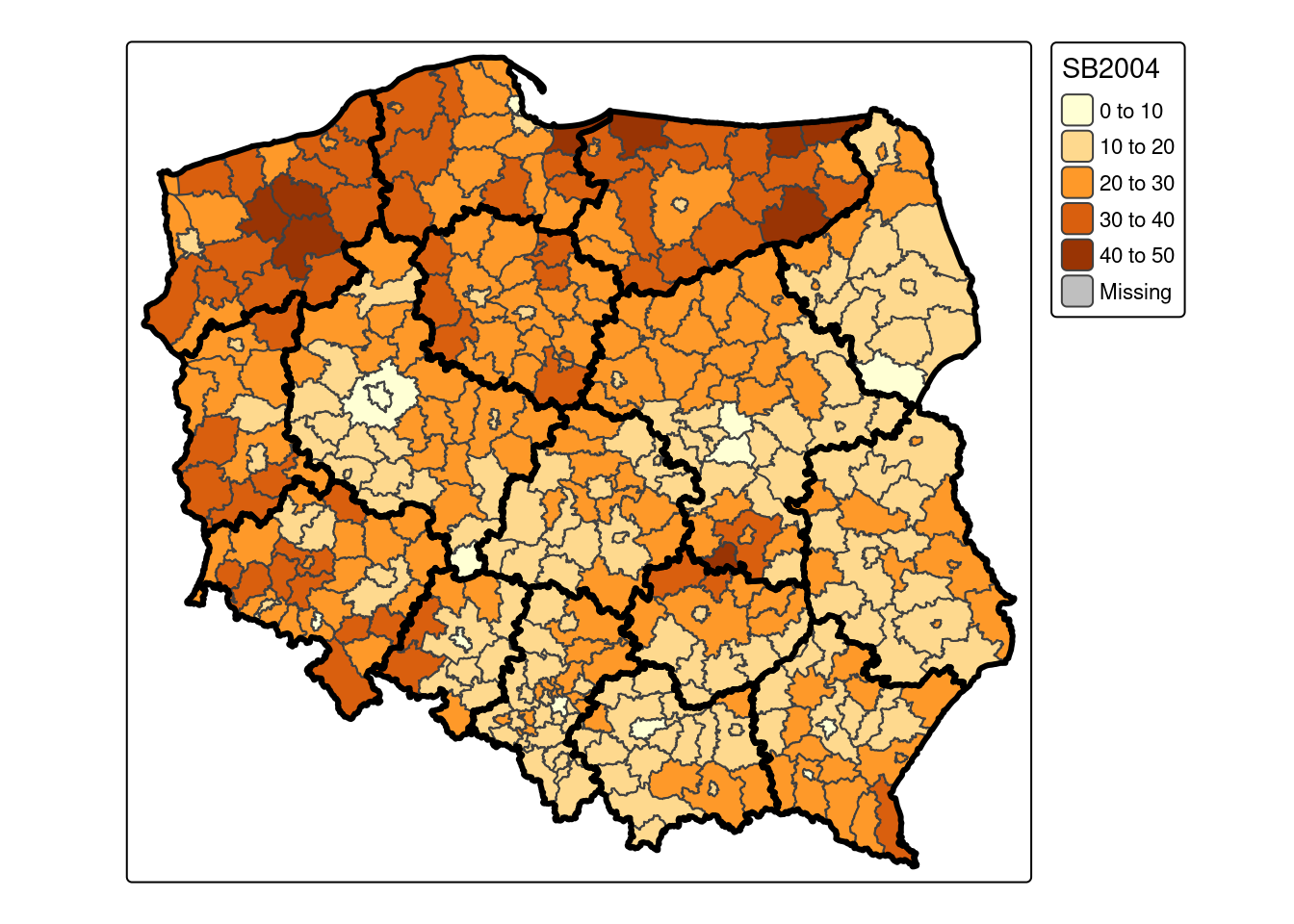

4.2 Miary autokorelacji przestrzennej

library(spdep)
#macierz sasiedztwa
nb_q = poly2nb(powiaty, queen = TRUE)
#macierz wag przestrzennych. 
lw = nb2listw(nb_q, style = "W")

#globalna statystyka Morana 
moran_test = moran.mc(powiaty$SB2004, listw = lw, nsim = 99)

# globalna statystyka C Geary'ego 
geary_test = geary.mc(powiaty$SB2004, listw = lw, nsim = 99)

#globalna statystyka Getisa i Orda 
g_test = globalG.test(powiaty$SB2004, listw = lw)

#lokalna statystyka Morana 
localmoran(powiaty$SB2004, listw = lw) |>  hotspot(Prname="Pr(z != E(Ii))", cutoff=0.05, p.adjust="none") -> powiaty$localI

# lokalna statystyka Geary'ego 
localC_perm(powiaty$SB2004, listw = lw, nsim = 99) |>  hotspot(Prname="Pr(z != E(Ci)) Sim", cutoff=0.05, p.adjust="none") -> powiaty$localC

# lokalna statstyka Getisa i Orda
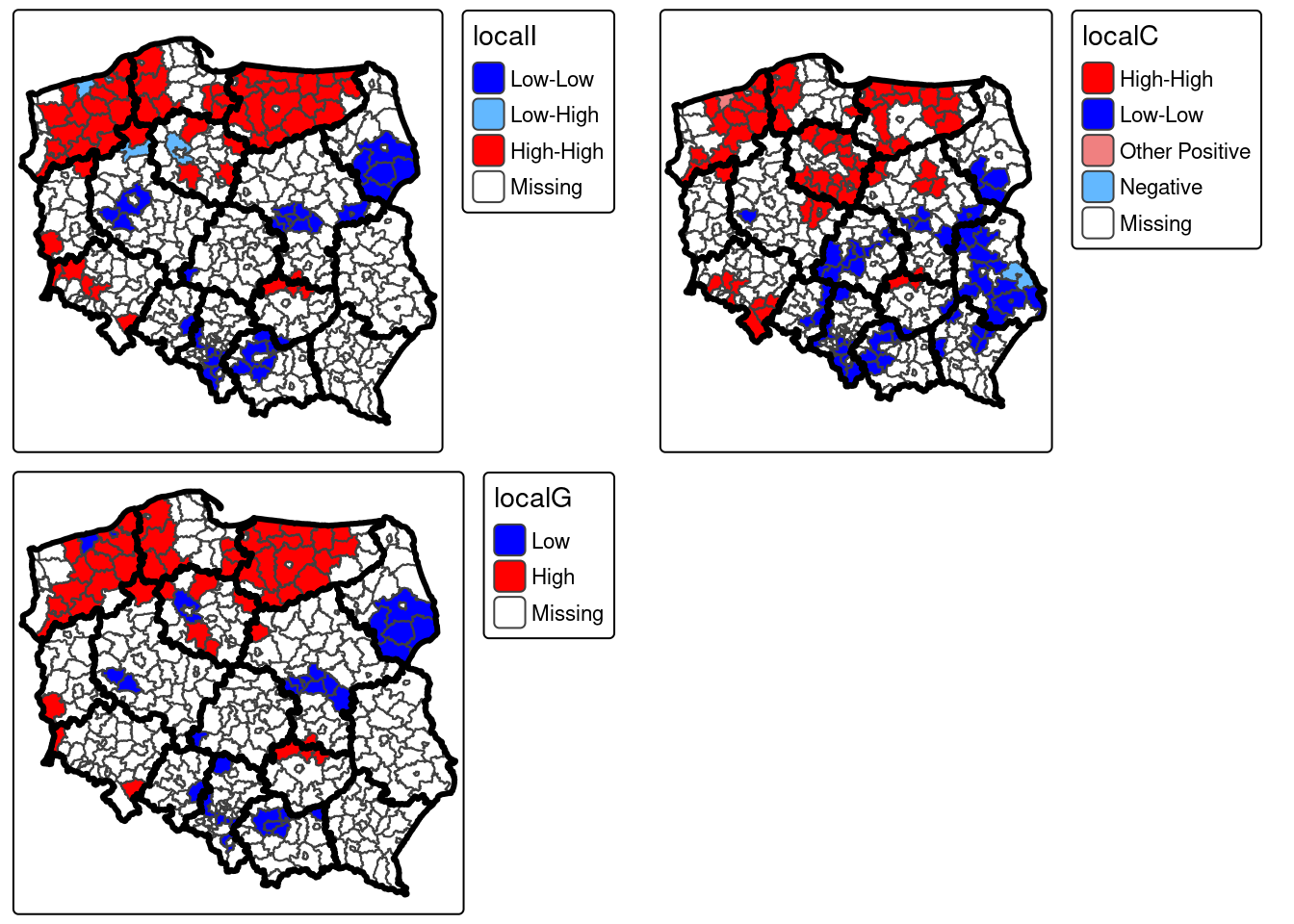
localG_perm(powiaty$SB2004, listw = lw, nsim = 99)|>  hotspot(Prname="Pr(z != E(Gi)) Sim", cutoff=0.05, p.adjust="none") -> powiaty$localG

4.3 Wizualizacja wyników

library(tmap)
#wizualizacja wyników

#local I
cluster_colors <- c("High-High"= "red", "High-Low" = "lightcoral", "Low-High" = "steelblue1", "Low-Low" = "blue")
MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$localI)]

tm_i = tm_shape(powiaty) + 
  tm_polygons("localI", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)

#local C
cluster_colors <- c("High-High"= "red", "Low-Low" = "blue",  "Other Positive" = "lightcoral", "Negative" = "steelblue1")
MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$localC)]

tm_c = tm_shape(powiaty) + 
  tm_polygons("localC", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)

#local G
cluster_colors <- c("Low" = "blue", "High"= "red")
MyPalette = cluster_colors[names(cluster_colors) %in% unique(powiaty$localG)]

tm_g  = tm_shape(powiaty) + 
  tm_polygons("localG", palette = MyPalette, colorNA = "white") + 
  tm_shape(woj_granica) + 
  tm_borders(col = "black", lwd = 3)

tmap_arrange(tm_i, tm_c, tm_g)

Statystyka przestrzenna	Interpretacja	Komenda w R
	MIARY GLOBALNE
Moran \(I\)	\(I > 0\) - dodatnia autokorelacja przestrzenna \(I < 0\) - ujemna autokorelacja przestrzenna \(I = 0\) - brak autokorelacji	moran() moran.test() moran.mc() moran.plot()
Geary \(C\)	\(0-1\) - dodatnia autokorelacja przestrzenna \(1-2\) - ujemna autokorelacja przestrzenna \(1\) - brak autokorelacji	geary() geary.test() geary.mc()
Getis & Ord \(G\)	testuje \(H_0\) o braku autokorelacji przestrzennej przeciwko \(H_A\) o dodatniej autokorelacji przestrzennej. Nie mierzy ujemnej autokorelacji przestrzennej.	globalG.test()
	MIARY LOKALNE
Local Moran \(I_{i}\)	\(I_{i} > 0\) - grupowanie podobnych wartości (wyższych lub niższych od średniej) \(I_{i} < 0\) - połączenie różnych wartości (np. wysokie wartości otoczone niskimi wartościami lub niskie wartości otoczone wysokimi wartościami)	local.moran()
Local Geary \(C_{i}\)	\(C_i < 0\) - niskie wartości wskazują na dodatnią autokorelację przestrzenną (podobieństwo regionu \(i\) z sąsiadami) \(C_i > 0\) - wysokie wartości wskazują na ujemną autokorelację przestrzenną, tj. region nie jest podobny do sąsiadów \(C_i = 0\) - brak autokorelacji przestrzennej	localC(), localC_perm()
Local \(G_{i}\)	\(G_{i} > 0\) - zgrupowanie regionów o relatywnie wysokich wartościach, klaster wysokich wartości (hot-spots) \(G_{i} < 0\) - zgrupowanie regionów o relatywnie niskich wartościach, klaster niskich wartości (cold-spots)	localG(), localG_perm()