Określanie sąsiedztwa danych poligonowych

library(sf)
library(tmap)
library(spdep)

1 Wprowadzenie

1.1 Jak określić czy dwa regiony ze sobą sąsiadują?

• kryterium wspólnej granicy obszarów (adjacency)

• kryterium odległości (odległość mierzona między centroidami obszarów):

  • macierz sąsiadów w promieniu d km
  • k najbliższych sąsiadów (knn)
  • odległość odwrotna (\(\frac{1}{d}\))

1.2 Sąsiedztwo obszarów - wspólna granica

Wspólną granicę obszarów można wyznaczyć posługując się regułą Rook lub Queen

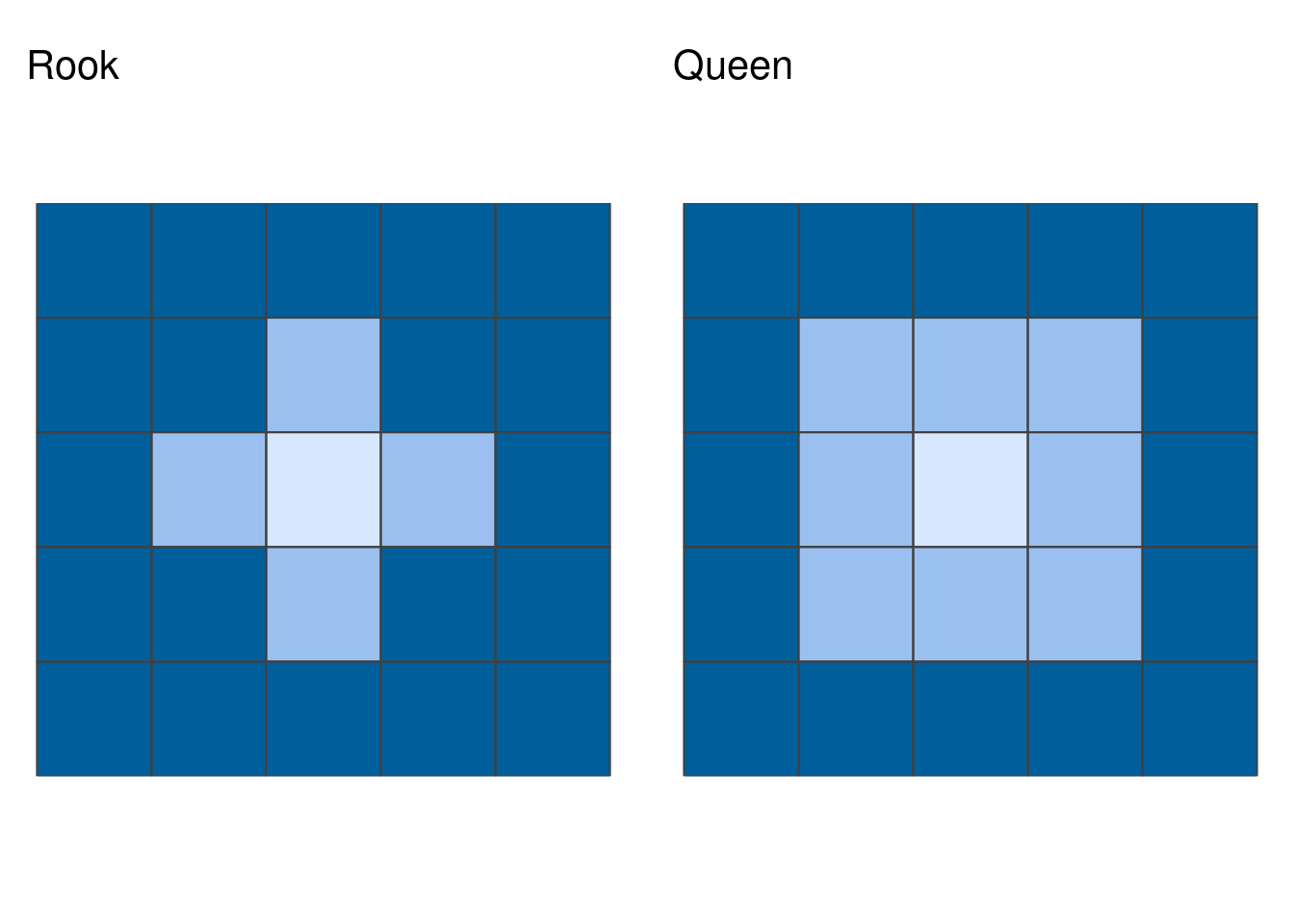
1.3 Macierz wag przestrzennych

• tabela NxN, w której przechowywane są informacje o występowaniu oraz sile zależności przestrzennych między obiektami (np. jednostkami administracyjnymi)
• Każdy element macierzy reprezentuje powiązanie między parą obszarów
• Ma zerową przekątną - jednostka nie ma wpływu na samą siebie (przynajmniej bezpośrednio)
• Formalna reprezentacja przestrzeni
• Podstawowa część wielu technik analizy przestrzennej, w tym autokorelacji przestrzennej, grupowania przestrzennego i regresji przestrzennej.

1.4 Tworzenie macierzy wag przestrzennych

1. Tworzymy macierz sąsiedztwa

• tabela, w której przechowywane są informacje o występowaniu (lub nie) relacji między obszarami (czy obszary ze sobą sąsiadują?).

• najprostsza forma: macierz binarna

\[ \begin{cases} 1 & \text{obiekt i jest sąsiadem obiektu j (mają wspólną granicę)} \\ 0 & \text{obiekt i nie jest sąsiadem obiektu j (nie mają wspólnej granicy)} \\ 0 & \text{elementy diagonalne macierzy} \\ \end{cases} \]

2. Dokonujemy standaryzacji macierzy sąsiedztwa

Najczęściej stosowaną standaryzacją jest standaryzacja wierszami do jedynki tak aby suma wag w każdym wierszu była równa 1

1.5 Macierze wag przestrzennych w R

Do utworzenia macierzy wag przestrzennych wykorzystuje się w R funkcje z pakietu spdep.

Dwie główne klasy z pakietu spdep:

• klasa "nb" - lista sąsiadów
• klasa "listw" - lista sąsiadów z wagami przestrzennymi dla wybranego schematu.

Możliwe jest przekształcenie tych klas w inne klasy i z powrotem, np:

• nb2mat() - funkcja generuje macierz wag przestrzennych dla listy sąsiadów dla dowolnego schematu kodowania wag.
• nb2listw() - funkcja uzupełnia listę sąsiadów o wartości wag wygenerowane dla dowolnego schematu kodowania.
• listw2mat() - funkcja przekształca listę sąsiadów z przypisanymi wagami w macierz.

Tworzenie macierzy sąsiedztwa:

• Na podstawie sąsiedztwa wyznaczanego przez wspólną granicę (funkcja poly2nb(), nb2listw())
• Na podstawie odległości (funkcja dnearneigh())
• Metoda k-najbliższych sąsiadów (funkcja knearneigh())
• Macierze sąsiedztwa dostarczone przez użytkownika (np. przy użyciu funkcji mat2listw())
• Odwrotność odległości

2 Przykład 1: Kryterium sąsiedztwa - wspólna granica

Tworzenie macierzy wag przestrzennych na podstawie kryterium wspólnej granicy wymaga wykonania w R 3 kroków:

• utworzenia listy sąsiadów (poly2nb())
• utworzenia listy zawierającej wagi (nb2listw)
• przekształcenia listy w macierz wag przestrzennych (listw2mat())

2.1 Dane

#wczytanie danych
library(sf)
ex = read_sf("data/area_ex.gpkg")
rownames(ex) <- ex$id
ex = ex[order(rownames(ex)),]
st_crs(ex) <- 2180

#wyswietlenie danych
tm_shape(ex) +
  tm_polygons(col = "grey", legend.show = FALSE) + 
  tm_text("id", size = 2)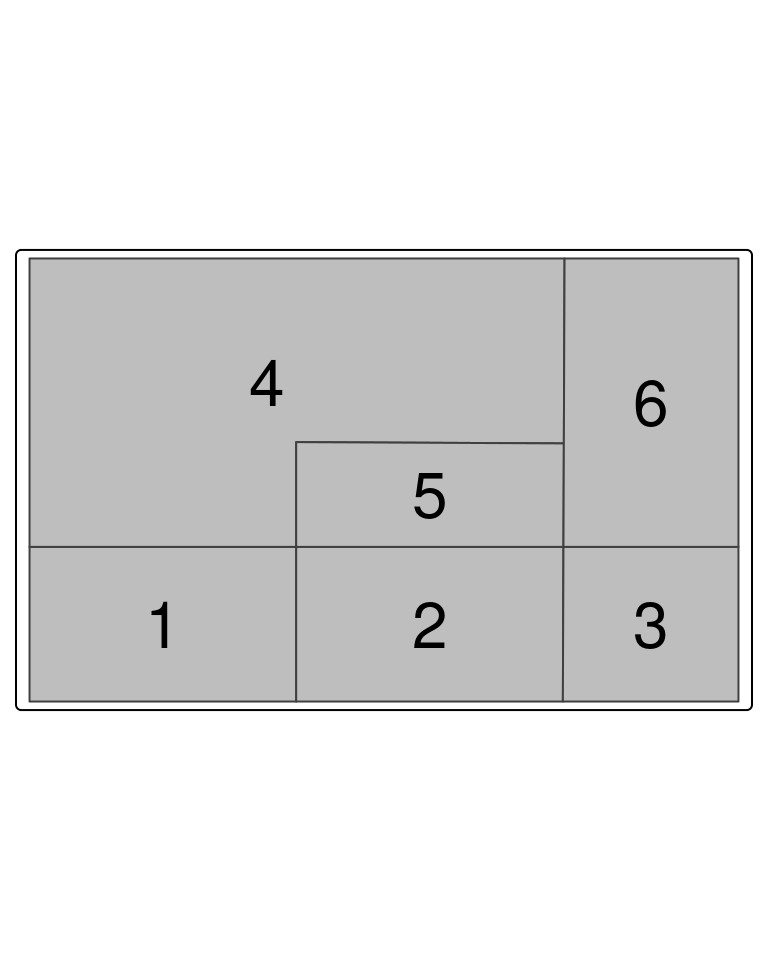

2.2 Utworzenie macierzy wag przestrzennych

• Tworzenie listy sąsiadów

Lista sąsiadów tworzona jest z wykorzystaniem funkcji poly2nb(). Funkcja ta tworzy listę sąsiadów na podstawie obiektu poligonowego wczytanego lub utworzonego za pomocą biblioteki sf. Pozwala ona na zdefiniowanie czy lista sąsiadów ma być tworzona z wykorzystaniem reguły Rook (opcja queen = FALSE) czy reguły Queen (queen = TRUE)

ex_nb = poly2nb(ex, queen = FALSE)
ex_nb

Neighbour list object:
Number of regions: 6 
Number of nonzero links: 12 
Percentage nonzero weights: 33.33333 
Average number of links: 2 

W wyniku otrzymamy listę sąsiadów dla każdego z obszarów. Poniższa lista składa się z 6 elementów (mamy 6 obszarów w zbiorze danych). Każdy element oznacza sąsiadów dla danego obszaru (np. obszar 1 wg reguły Rook ma dwóch sąsiadów: obszar nr 2 oraz obszar nr 4).

str(ex_nb)

List of 6
 $ : int [1:2] 2 4
 $ : int [1:3] 1 3 5
 $ : int [1:2] 2 6
 $ : int [1:2] 1 5
 $ : int [1:2] 2 4
 $ : int 3
 - attr(*, "class")= chr "nb"
 - attr(*, "region.id")= chr [1:6] "1" "2" "3" "4" ...
 - attr(*, "call")= language poly2nb(pl = ex, queen = FALSE)
 - attr(*, "type")= chr "rook"
 - attr(*, "snap")= num 0.01
 - attr(*, "sym")= logi TRUE
 - attr(*, "ncomp")=List of 2
  ..$ nc     : int 1
  ..$ comp.id: int [1:6] 1 1 1 1 1 1

• Tworzenie macierzy sąsiedztwa

Funkcja nb2listw() uzupełnia listę sąsiadów o wagi przestrzenne dla wybranego schematu kodowania (patrz opcje dla argumentu style) style = "B" oznacza, że chcemy utworzyć macierz binarną.

ex_lw = nb2listw(ex_nb, style = "B")
ex_lw

Characteristics of weights list object:
Neighbour list object:
Number of regions: 6 
Number of nonzero links: 12 
Percentage nonzero weights: 33.33333 
Average number of links: 2 

Weights style: B 
Weights constants summary:
  n nn S0 S1  S2
B 6 36 12 24 104

Funkcja listsw2mat() przekształca listę na macierz. W wyniku otrzymamy macierz binarną, gdzie 1 oznacza, że obiekty ze sobą sąsiadują, a 0 oznacza brak sąsiedztwa między obszarami

ex_mat = listw2mat(ex_lw)
ex_mat

  [,1] [,2] [,3] [,4] [,5] [,6]
1    0    1    0    1    0    0
2    1    0    1    0    1    0
3    0    1    0    0    0    1
4    1    0    0    0    1    0
5    0    1    0    1    0    0
6    0    0    1    0    0    0

• Tworzenie macierzy wag przestrzennych

Argument style = "W" tworzy macierz wag przestrzennych, gdzie wagi są standaryzowane wierszami (wagi w każdym wierszu sumują się do 1).

ex_lwp = nb2listw(ex_nb, style = "W")
ex_mat_wp = listw2mat(ex_lwp)
ex_mat_wp

       [,1] [,2]      [,3] [,4]      [,5] [,6]
1 0.0000000  0.5 0.0000000  0.5 0.0000000  0.0
2 0.3333333  0.0 0.3333333  0.0 0.3333333  0.0
3 0.0000000  0.5 0.0000000  0.0 0.0000000  0.5
4 0.5000000  0.0 0.0000000  0.0 0.5000000  0.0
5 0.0000000  0.5 0.0000000  0.5 0.0000000  0.0
6 0.0000000  0.0 1.0000000  0.0 0.0000000  0.0

Utwórz macierz sąsiedztwa oraz macierz wag przestrzennych dla sąsiedztwa poligonów wyznaczonego regułą Queen.

3 Przykład 2: Sąsiedztwo obszarów - powiaty województwa wielkopolskiego

3.1 Dane

powiaty = read_sf("data/wlkp_powiaty.gpkg")
tm_shape(powiaty) + tm_polygons(fill = "grey", col = "black")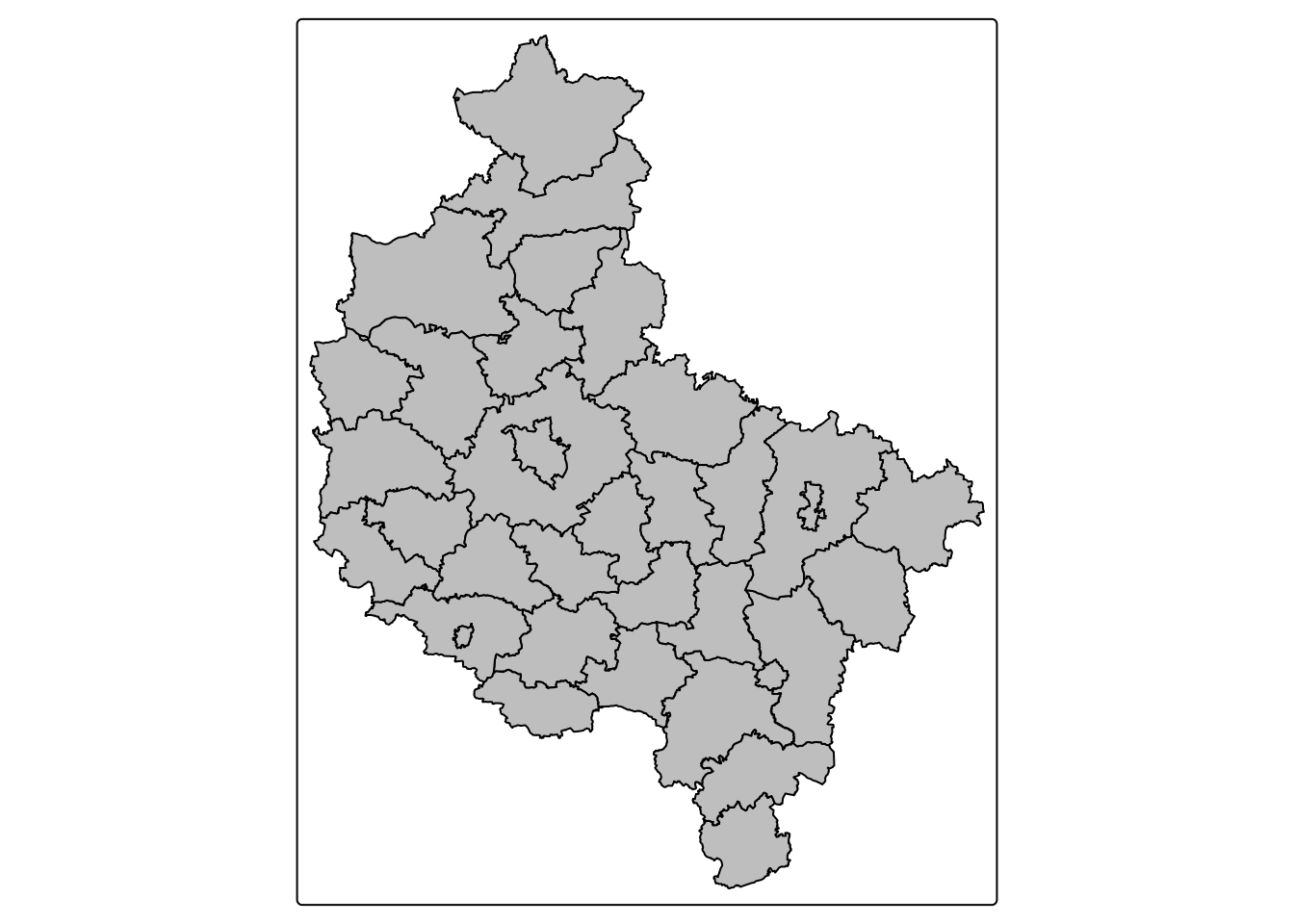

3.2 Sąsiedztwo: krytetium wspólnej granicy

W poniższym przykładzie dla każdego z powiatów w województwie wielkopolskim wyznaczono sąsiadów posługując się kryterium wspólnej granicy (określonej poprzez regułę Queen)

#lista sąsiadów
powiaty_nb_q = poly2nb(powiaty, queen = TRUE, row.names = as.character(powiaty$Nazwa))
#macierz binarna, aby otrzymać macierz standaryzowaną wierszami należy podac style = "W"
powiaty_lw = nb2listw(powiaty_nb_q, style = "B")
powiaty_mat = listw2mat(powiaty_lw)
colnames(powiaty_mat) <- as.character(powiaty$Nazwa)

Macierz sąsiedztwa powiatów w województwie wielkopolskim

powiaty_mat[1:5, 1:5]

                        chodzieski czarnkowsko-trzcianecki gnieźnieński
chodzieski                       0                       1            0
czarnkowsko-trzcianecki          1                       0            0
gnieźnieński                     0                       0            0
gostyński                        0                       0            0
grodziski                        0                       0            0
                        gostyński grodziski
chodzieski                      0         0
czarnkowsko-trzcianecki         0         0
gnieźnieński                    0         0
gostyński                       0         0
grodziski                       0         0

Poniższy kod pozwala na wypisanie sąsiadów dla danego powiatu

powiat_nazwy = as.character(powiaty$Nazwa)
powiat_nazwy[powiaty_nb_q[[which(powiat_nazwy=="poznański")]]]

 [1] "gnieźnieński" "grodziski"    "kościański"   "nowotomyski"  "obornicki"   
 [6] "Poznań"       "szamotulski"  "średzki"      "śremski"      "wągrowiecki" 
[11] "wrzesiński"  

Z jakimi powiatami graniczy powiat koniński?

Z jakimi powiatami graniczy powiat pilski?

Wizualizacja macierzy sąsiedztwa

#wyznaczenie centroidów dla powiatów 
powiaty_cen = st_centroid(st_geometry(powiaty), of_largest_polygon = FALSE)
#konwersja listy sąsiadów na obiekt liniowy (linie łączące sąsiadujące powiaty)
powiaty_nb_net = st_as_sf(nb2lines(powiaty_nb_q, coords = st_coordinates(powiaty_cen)))

Warning in CRS(proj4string): CRS: projargs should not be NULL; set to NA

st_crs(powiaty_nb_net)<- 2180
#wizualizacja
tm_shape(powiaty) + tm_polygons() + 
  tm_shape(powiaty_nb_net) + tm_lines() + tm_shape(powiaty_cen) + tm_dots(size =0.6 , col = "black")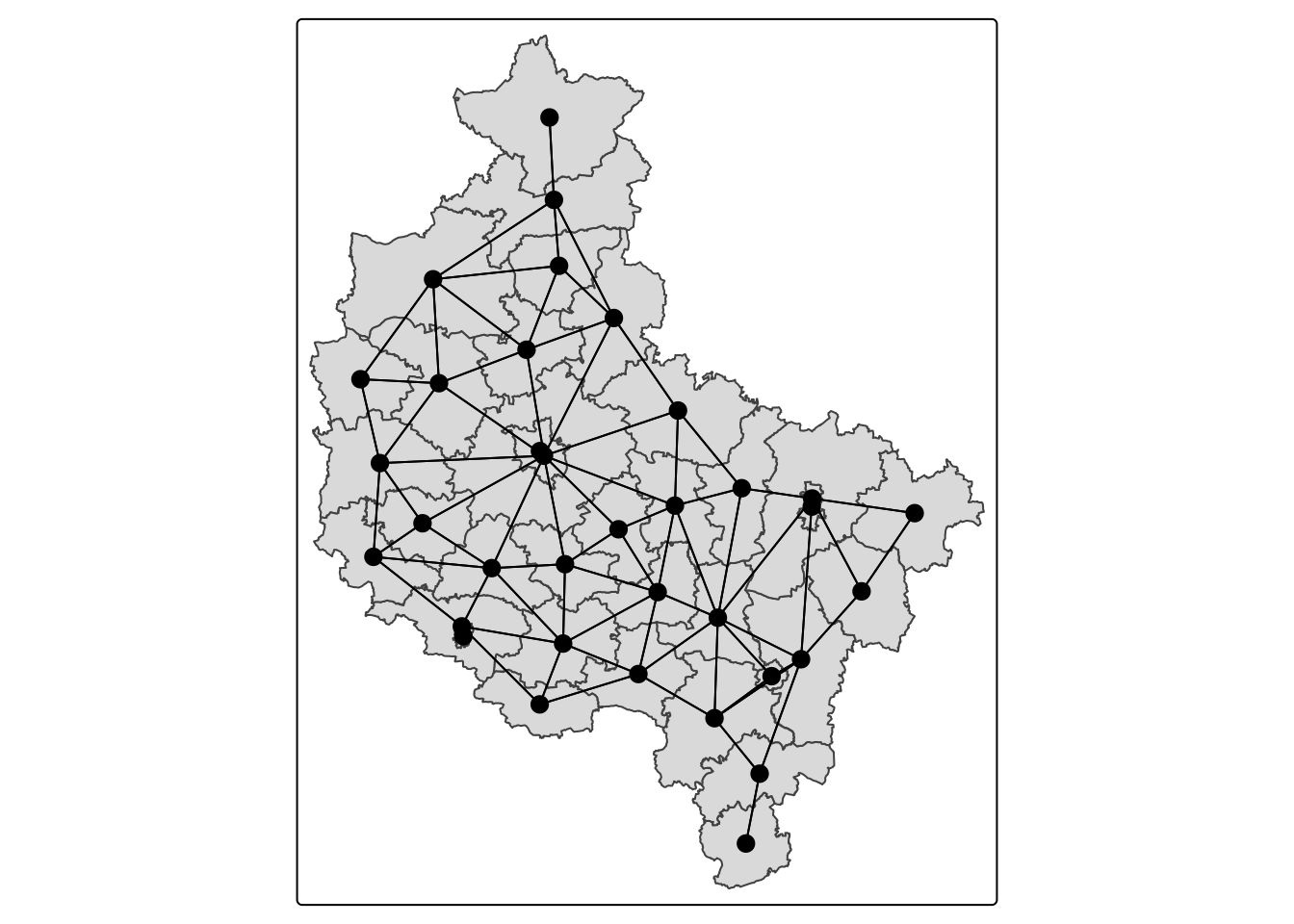

3.3 Sąsiedztwo: krytetium odległości

• odległość między obszarami jest mierzona między centroidami obszarów.
• sąsiadem będzie obiekt, którego środek jest oddalony w linii prostej o nie więcej niż d km.

Analiza odległości centroidami sąsiadujących powiatów

#centroidy powiatów
powiaty_cen = st_centroid(st_geometry(powiaty), of_largest_polygon = FALSE)
#lista sąsiadów wg kryterium sąsiedztwa 
powiaty_nb_q = poly2nb(powiaty, queen = TRUE, row.names = as.character(powiaty$Nazwa))
#obliczenie odległosci między sąsiadami, obiekt powiaty_dists zwraca odległosc euklidesową między centroidami sąsiadujących powiatów
powiaty_dists = nbdists(powiaty_nb_q, powiaty_cen)
head(powiaty_dists, 2)

[[1]]
[1] 42356.78 30099.31 22127.30 25311.28

[[2]]
[1] 42356.78 41310.84 39130.37 48353.71 34813.16

powiaty_dists_vec = unlist(powiaty_dists)

Poniższy histogram pokazuje rozkład odległości między centroidami sąsiadujących powiatów.

hist(powiaty_dists_vec)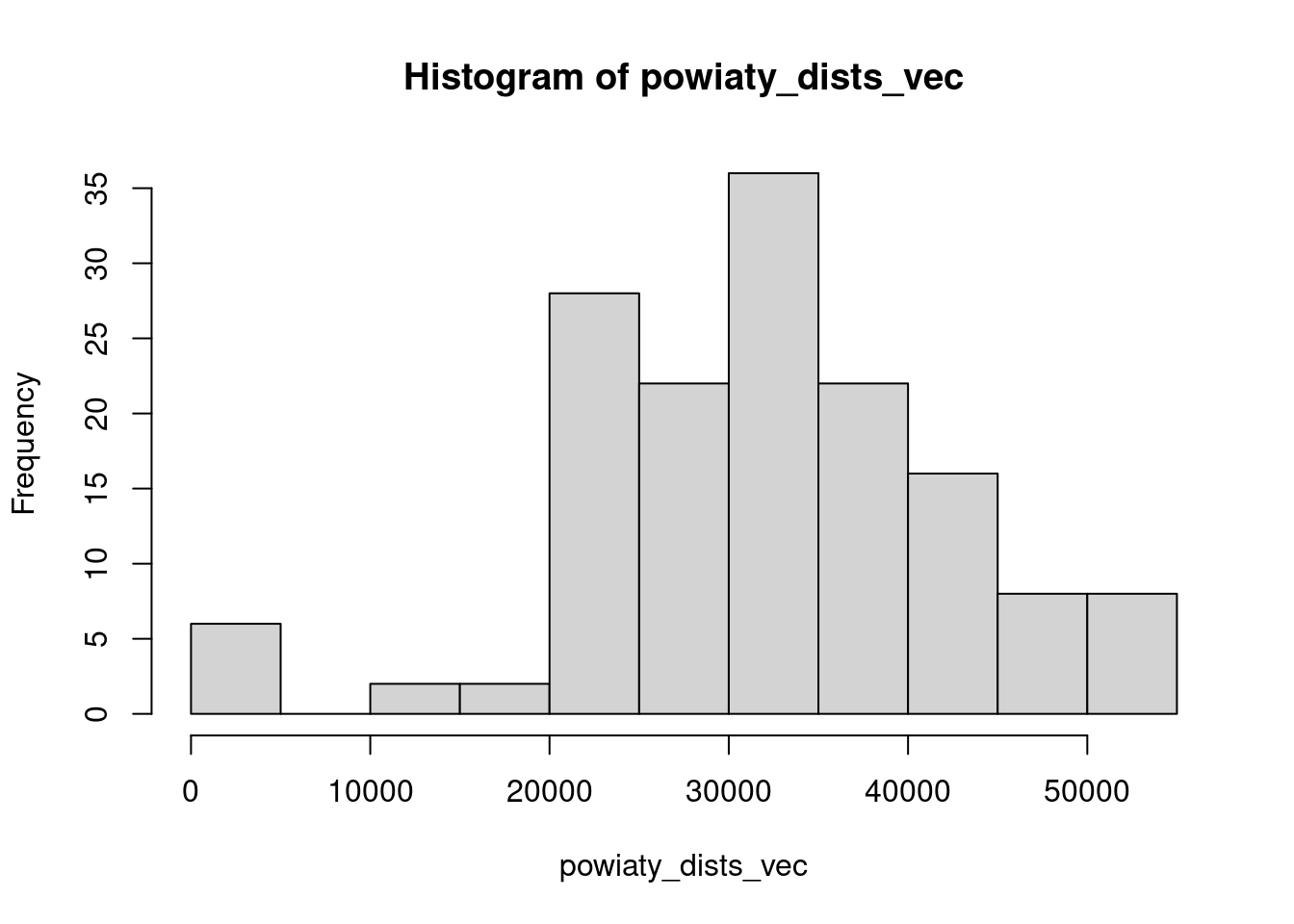

Poniżej obliczone zostały statystyki opisowe dla odległości euklidesowej między centroidami sąsiadujących powiatów.

summary(powiaty_dists_vec)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   2063   24892   31809   31915   37644   54911 

Macierz sąsiedztwa na podstawie kryterium odległości

Funkcja dnearneigh() identyfikuje sąsiadów na podstawie zadanej odległości. W poniższym przykładzie za sąsiadów zostaną uznane powiaty, których centroidy w linii prostej (odległość euklidesowa) są od siebie oddalone o 0 do 30000 m.

powiaty_nb_d = dnearneigh(powiaty_cen, d1 = 0, d2 = 30000, longlat = FALSE, row.names = as.character(powiaty$Nazwa))

Warning in dnearneigh(powiaty_cen, d1 = 0, d2 = 30000, longlat = FALSE, :
dnearneigh: longlat argument overrides object

Warning in dnearneigh(powiaty_cen, d1 = 0, d2 = 30000, longlat = FALSE, :
neighbour object has 8 sub-graphs

powiaty_nb_d

Neighbour list object:
Number of regions: 35 
Number of nonzero links: 64 
Percentage nonzero weights: 5.22449 
Average number of links: 1.828571 
5 regions with no links:
czarnkowsko-trzcianecki, gnieźnieński, kolski, obornicki, turecki
8 disjoint connected subgraphs

powiaty_mat2 = nb2mat(powiaty_nb_d, zero.policy = TRUE)
colnames(powiaty_mat2) <- as.character(powiaty$Nazwa)
powiaty_mat2[1:5, 1:5]

                        chodzieski czarnkowsko-trzcianecki gnieźnieński
chodzieski                       0                       0            0
czarnkowsko-trzcianecki          0                       0            0
gnieźnieński                     0                       0            0
gostyński                        0                       0            0
grodziski                        0                       0            0
                        gostyński grodziski
chodzieski                      0         0
czarnkowsko-trzcianecki         0         0
gnieźnieński                    0         0
gostyński                       0         0
grodziski                       0         0

Wizualizacja sąsiedztwa

• Wizualizacja sąsiedztwa używając funkcji plot()

plot(st_geometry(powiaty), border = "grey", lwd = 1.5, cex = 3)
plot(powiaty_nb_d, coords = st_coordinates(powiaty_cen), add = TRUE, lwd = 1.5)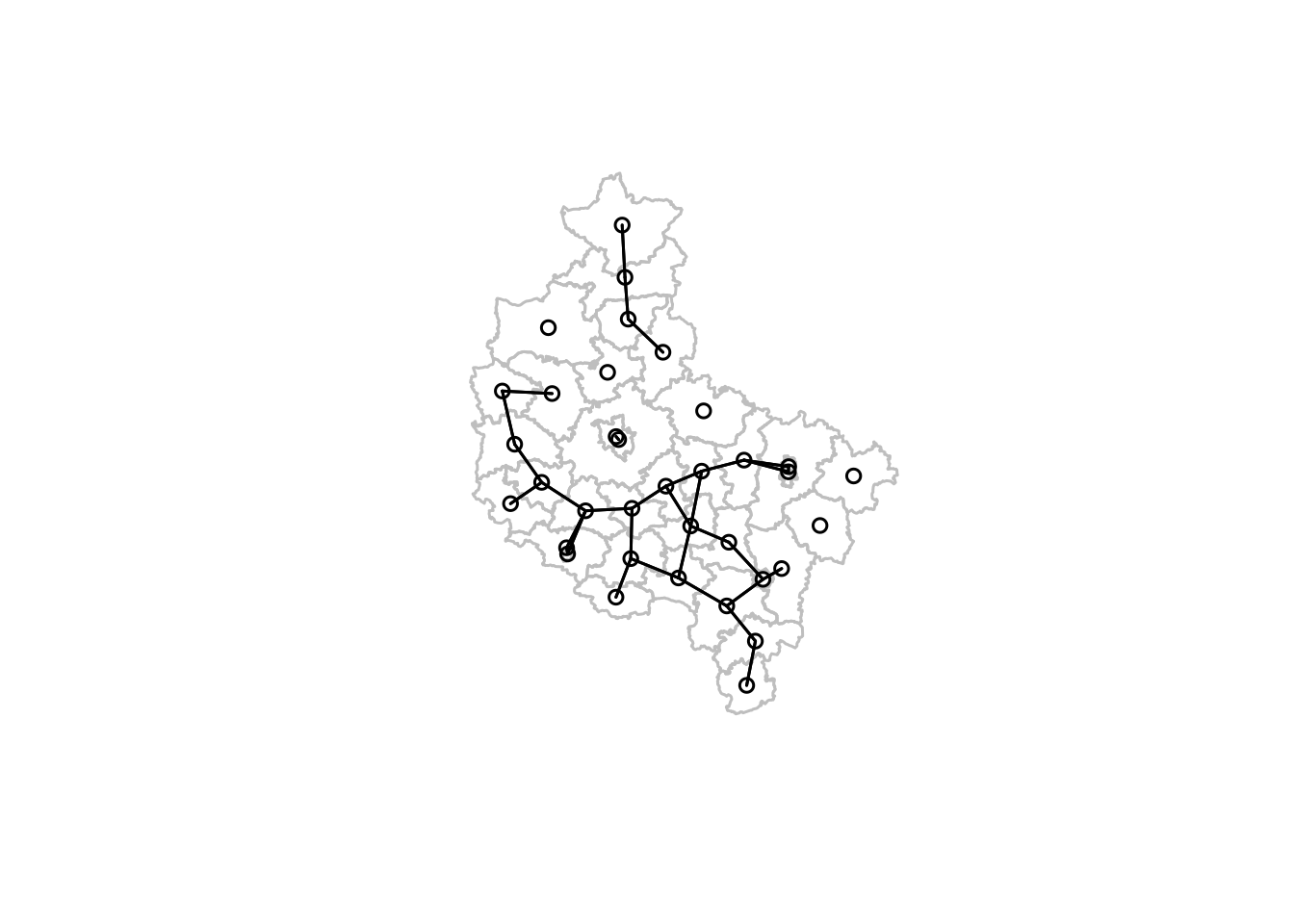

• Wizualizacja sąsiedztwa używając pakietu tmap()

#przekształcenie obiektu klasy nb na obiekt klasy sf
powiaty_nb_d_net = st_as_sf(nb2lines(powiaty_nb_d, coords = st_coordinates(powiaty_cen)))
st_crs(powiaty_nb_d_net)<- 2180
#wizualizacja
tm_shape(powiaty) + tm_polygons() + 
  tm_shape(powiaty_nb_d_net) + tm_lines() + tm_shape(powiaty_cen) + tm_dots(size =0.6 , col = "black")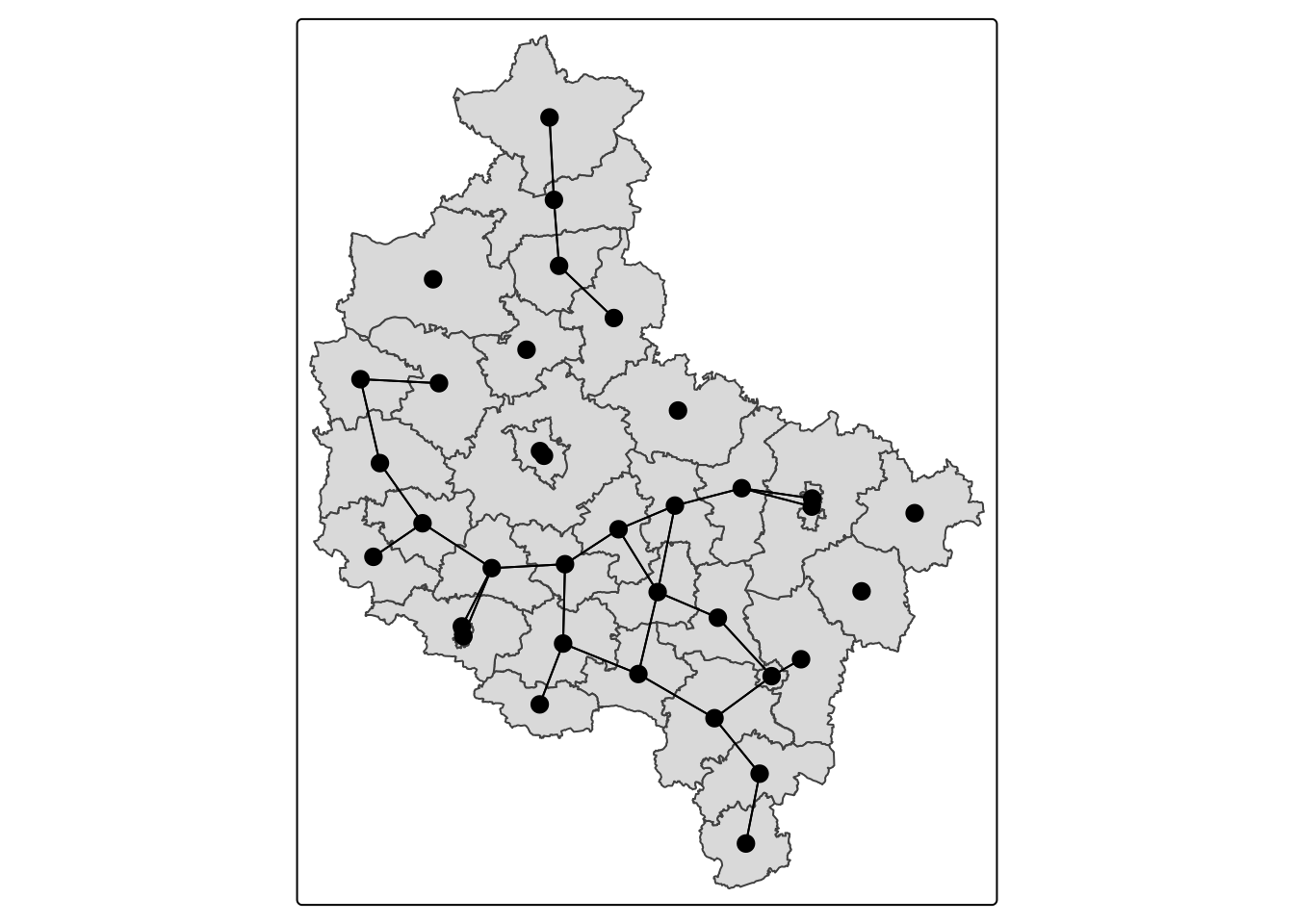

Poniższy kod pozwala na wypisanie sąsiadów dla danego powiatu.

• Jakie powiaty sąsiadują z powiatem Poznań?

powiat_nazwy = as.character(powiaty$Nazwa)
powiat_nazwy[powiaty_nb_d[[which(powiat_nazwy=="Poznań")]]]

[1] "poznański"

• Jakie powiaty sąsiadują z powiatem Kalisz?

powiat_nazwy[powiaty_nb_d[[which(powiat_nazwy=="Kalisz")]]]

[1] "kaliski"    "ostrowski"  "pleszewski"

Jakie powiaty sąsiadują z powiatem konińskim biorąc pod uwagę kryterium odległości (30km)?

3.4 Sąsiedztwo: k-najbliższych sąsiadów

• tworzona dla danych punktowych

• używając danych obszarowych należy najpierw wyznaczyć ich centroidy

• najbliższy sąsiad to obszar którego środek leży najbliżej środka danego obszaru stosując odległość euklidesową.

  • na liczbę najbliższych sąsiadów ma zatem wpływ wielkość oraz kształt regionu i regionów sąsiednich

Funkcja knearneigh() wyznacza k najbliższych sąsiadów na podstawie odległości między centroidami powiatów.

powiaty_cen = st_centroid(st_geometry(powiaty), of_largest_polygon = FALSE)
powiaty_knn = knearneigh(powiaty_cen, k = 5)
powiaty_nb_knn = knn2nb(powiaty_knn)
powiaty_nb_knn[1:3]

[[1]]
[1]  2 19 22 32 35

[[2]]
[1]  1 17 19 22 28

[[3]]
[1] 25 27 29 32 34

Każdy element listy odnosi się do powiatu, np. [[1]] oznacza powiat chodzieski, a poszczególne elementy wskazują id powiatów, z które stanowią 5 najbliższych sąsiadów. Dla powiatu chodzieskiego będą to powiaty:

powiaty$Nazwa[rownames(powiaty)%in%c(2, 19 ,22, 32, 35)]

[1] "czarnkowsko-trzcianecki" "obornicki"              
[3] "pilski"                  "wągrowiecki"            
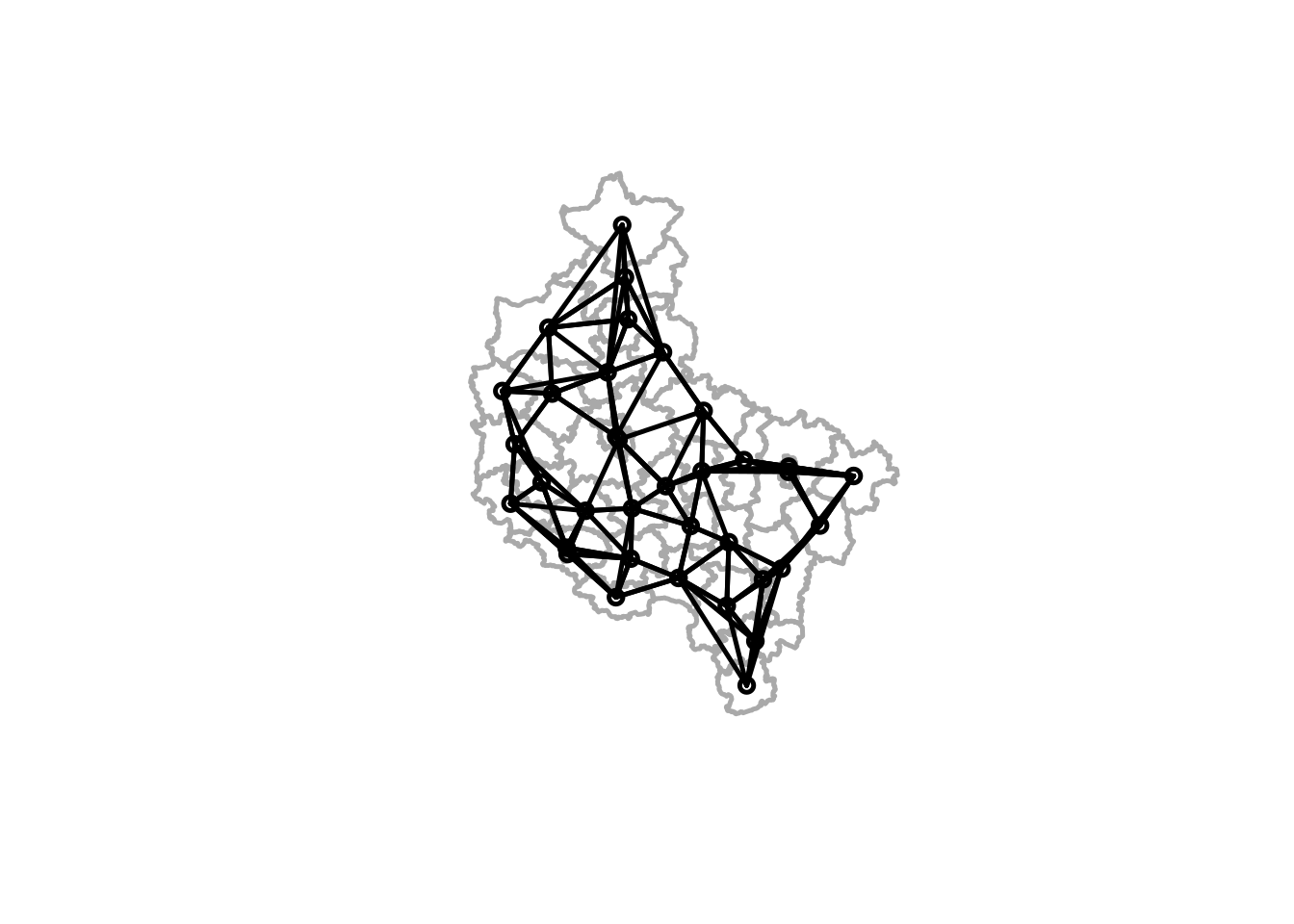
[5] "złotowski"              

plot(st_geometry(powiaty), border = "darkgrey", lwd = 2.5, cex = 3)
plot(powiaty_nb_knn, coords = st_coordinates(powiaty_cen), add = TRUE, lwd = 2.5)