library(sf)
library(sfnetworks)
library(tmap)
library(tidygraph)
library(dplyr)Miary grafu
1 Miary grafu
Sieć geoprzestrzenną określa się jako graf osadzony w przestrzeni geograficznej, w którym wierzchołki i krawędzie można przedstawić jako obiekty geograficzne. Taką sieć można także opisać stosując różne miary grafu.
1.1 Miary centralności wierzchołka
Miary centralności wierzchołka określają, który wierzchołek jest najbardziej istotny w analizowanym grafie/sieci.
Wyróżnia się następujęce miary:
stopień wierzchołka (degree centrality) - liczba bezpośrednich połączeń wierzchołka z innymi wierzchołkami sieci. Obliczana jest z wykorzystaniem funkcji
tidygraph::centrality_degree().miara bliskości/sąsiedztwa (closeness centrality) - określa średnią odległość rozpatrywanego wierzchołka do wszystkich pozostałych wierzchołków w grafie. Obliczana jest z wykorzystaniem funkcji
tidygraph::centrality_closeness().miara pośrednictwa/obciążenia wierzchołka (betweenness centrality) - liczba najkrótszych ścieżek przechodzących przez wierzchołek. Obliczana jest z wykorzystaniem funkcji
tidygraph::centrality_betweenness().
1.2 Miary krawędzi
Miary krawędzi opisują krawędzie grafu. Wyróżnia się:
długość krawędzi - obliczana jest z wykorzystaniem funkcji
sf::st_length(geometry).pośrednictwo krawędzi (betweenness) - liczba najkrótszych ścieżek przechodzących przez krawędź. Obliczana jest z wykorzystaniem funkcji
tidygraph::centrality_edge_betweenness().
1.3 Miary strukturalne grafu
Miary strukturalne grafu charakteryzują cały graf/sieć. Wyróżnia się miary:
średni stopnień wierzchołka grafu (average degree)
gęstość grafu (density) - określa, ile powiązań istnieje między wierzchołkami w porównaniu do tego, ile powiązań między wierzchołkami jest możliwych. Obliczana za pomocą funkcji
igraph::edge_density()średnica grafu (diameter) - podaje długość (w liczbie krawędzi) najdłuższej ścieżki pomiędzy dwoma dowolnymi połączonymi wierzchołkami (jest to najdłuższa odległość wśród najkrótszych ścieżek). Obliczana za pomocą funkcji
with_graph(net, graph_diameter())współczynnik klasteryzacji (clustering coefficient) - odzwierciedla stopień, w jakim wierzchołki w grafie mają tendencję do grupowania się. Obliczana za pomocą funkcji
with_graph(net, graph_mean_dist())średnia odległość (mean distance) - średnia długość najkrótszej drogi. Obliczana za pomocą funkcji
igraph::transitivity(net, type = "global")
2 Przykład: Miary grafu w R
W przykładzie wykorzystamy sieć przestrzenną reprezentowaną przez sieć ulic w centrum Poznania.
foot_lines = read_sf("data/out_osm_lines.gpkg")net = as_sfnetwork(foot_lines)plot(net)
2.1 Miary centralności wierzchołka
Miary centralności wierzchołka opisują znaczenie węzłów w sieci.
2.1.1 Stopień centralności wierzchołka
Najprostszą z tych miar jest stopień centralności wierzchołka: liczba bezpośrednich połączeń wierzchołka z innymi wierzchołkami sieci. Stopień centralności wierzchołka można obliczyć zliczając liczbę krawędzi połączonych z węzłem. Im wyższa wartość tym węzeł ma większe znaczenie w sieci.
Obliczenie miar centralności wierzchołka w R wymaga:
- aktywowania tabeli zawierającej wierzchołki (activate(“nodes”))
- dodania do tabeli kolumny, w której zostanie obliczona wartość danej miary centralności (np. mutate(degree = centrality_degree()))
- konwersja sieci na obiekt klasy
sf, aby można było go zwizualizować.
Stopień centralności wierzchołka obliczany jest za pomocą funkcji tidygraph::centrality_degree().
net = net |> activate("nodes") |> mutate(degree = centrality_degree())
nodes_sf = st_as_sf(net)net# A sfnetwork with 1541 nodes and 1130 edges
#
# CRS: ETRF2000-PL / CS92
#
# A directed multigraph with 657 components with spatially explicit edges
#
# A tibble: 1,541 × 2
geom degree
<POINT [m]> <dbl>
1 (359112.5 506465.9) 1
2 (359138.6 506532.7) 0
3 (359193.2 506680.9) 1
4 (359274.8 506675) 2
5 (359023.2 506483.5) 1
6 (359048.9 506476.2) 1
# ℹ 1,535 more rows
#
# A tibble: 1,130 × 7
from to osm_id name highway foot geom
<int> <int> <chr> <chr> <chr> <chr> <LINESTRING [m]>
1 1 2 8452538 Aleje Karola Mar… living… <NA> (359112.5 506465.9, 3591…
2 3 4 8452541 Ignacego Paderew… living… yes (359193.2 506680.9, 3592…
3 5 6 20910211 Święty Marcin living… <NA> (359023.2 506483.5, 3590…
# ℹ 1,127 more rowsplot(nodes_sf["degree"])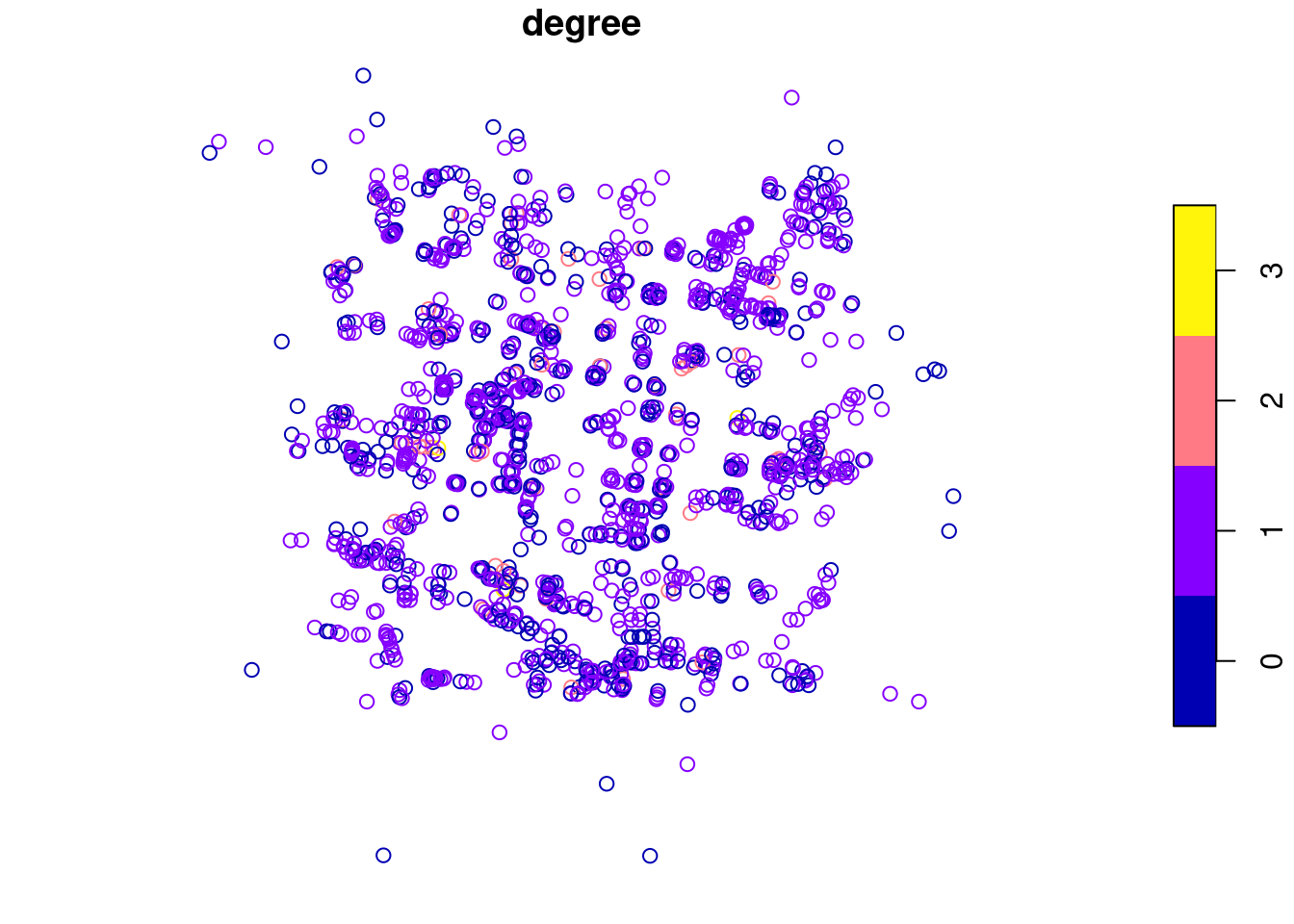
2.1.2 Miara bliskości (sąsiedztwa)
Innym przykładem miary centralności wierzchołka jest miara bliskości (sąsiedztwa, closeness centrality). Miara ta określa średnią odległość rozpatrywanego wierzchołka do wszystkich pozostałych wierzchołków w grafie. Wierzchołek, który “średnio rzecz biorąc” jest najbliższy wszystkim wierzchołkom jest uznawany za najistotniejszy.
Miara bliskości obliczana jest za pomocą funkcji tidygraph::centrality_closeness().
net = net |> activate("nodes") |> mutate(closeness = centrality_closeness())
nodes_sf = st_as_sf(net)
plot(nodes_sf["closeness"])
2.1.3 Miara pośrednictwa
Innym przykładem jest miara pośrednictwa/obciążenia wierzchołka (betweenness centrality), która, mówiąc najprościej, jest liczbą najkrótszych ścieżek przechodzących przez węzeł. Usunięcie wierzchołka z wysoką wartością miary pośrednicywa spowoduje, że obliczenia najkrótszej ścieżki będą dłuższe dla wielu innych wierzchołków w sieci. W efekcie spowoduje to największe zakłócenia w działaniu sieci.
Miara pośrednictwa obliczana jest za pomocą funkcji tidygraph::centrality_betweenness().
net = net |> activate("nodes") |> mutate(betweenness = centrality_betweenness())
nodes_sf = st_as_sf(net)
plot(nodes_sf["betweenness"])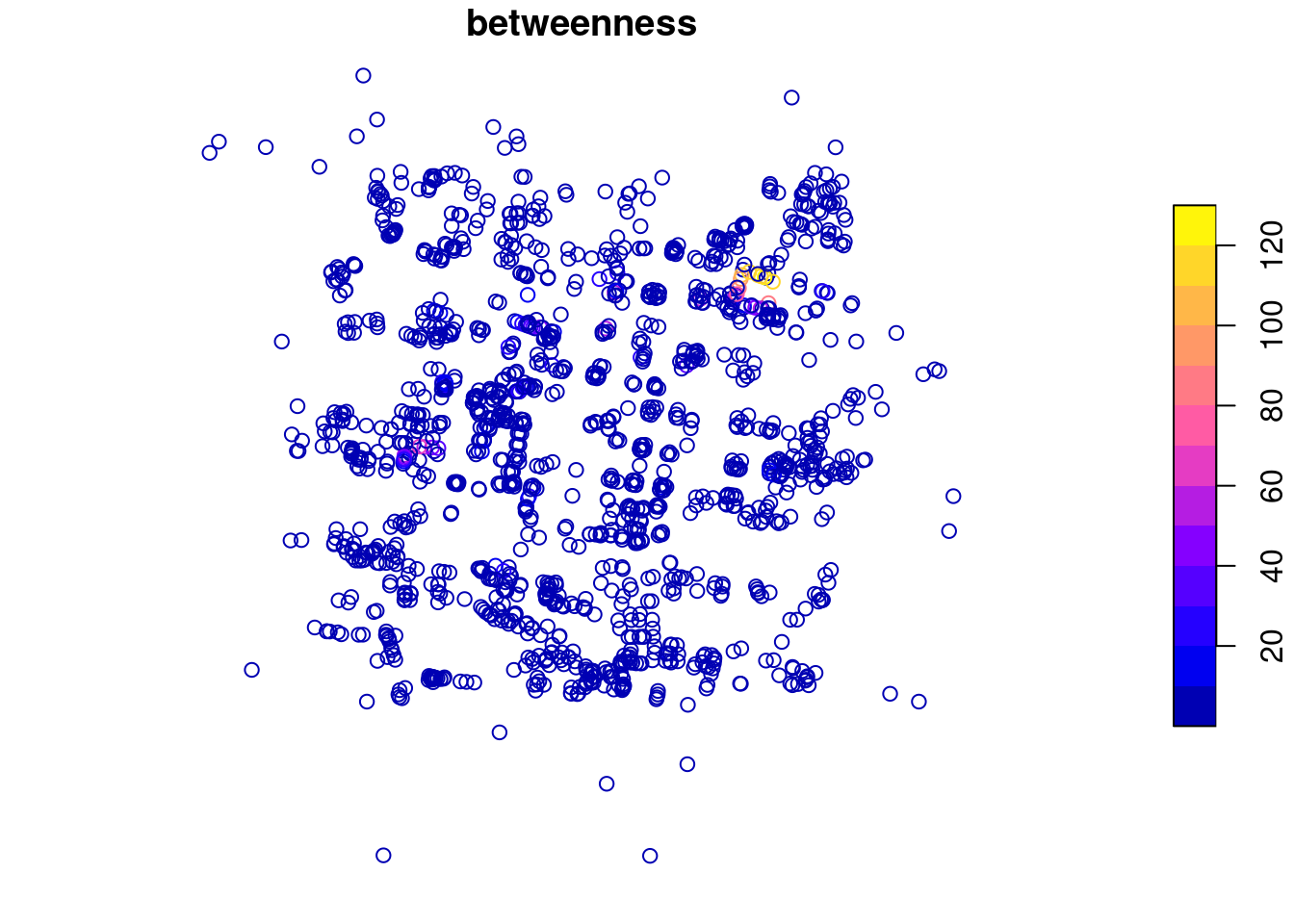
2.2 Miary krawędzi
Obliczenie miar krawędzi wymaga aktywowania tabeli przechowującej informacje o krawędziach.
net |> activate("edges") 2.2.1 Długość krawędzi
Jedną z miar opisujących krawędzie (segmenty sieci) jest ich długość.
net = net |> activate("edges") |> mutate(length = st_length(geom))
edge_sf = st_as_sf(net)
plot(edge_sf["length"])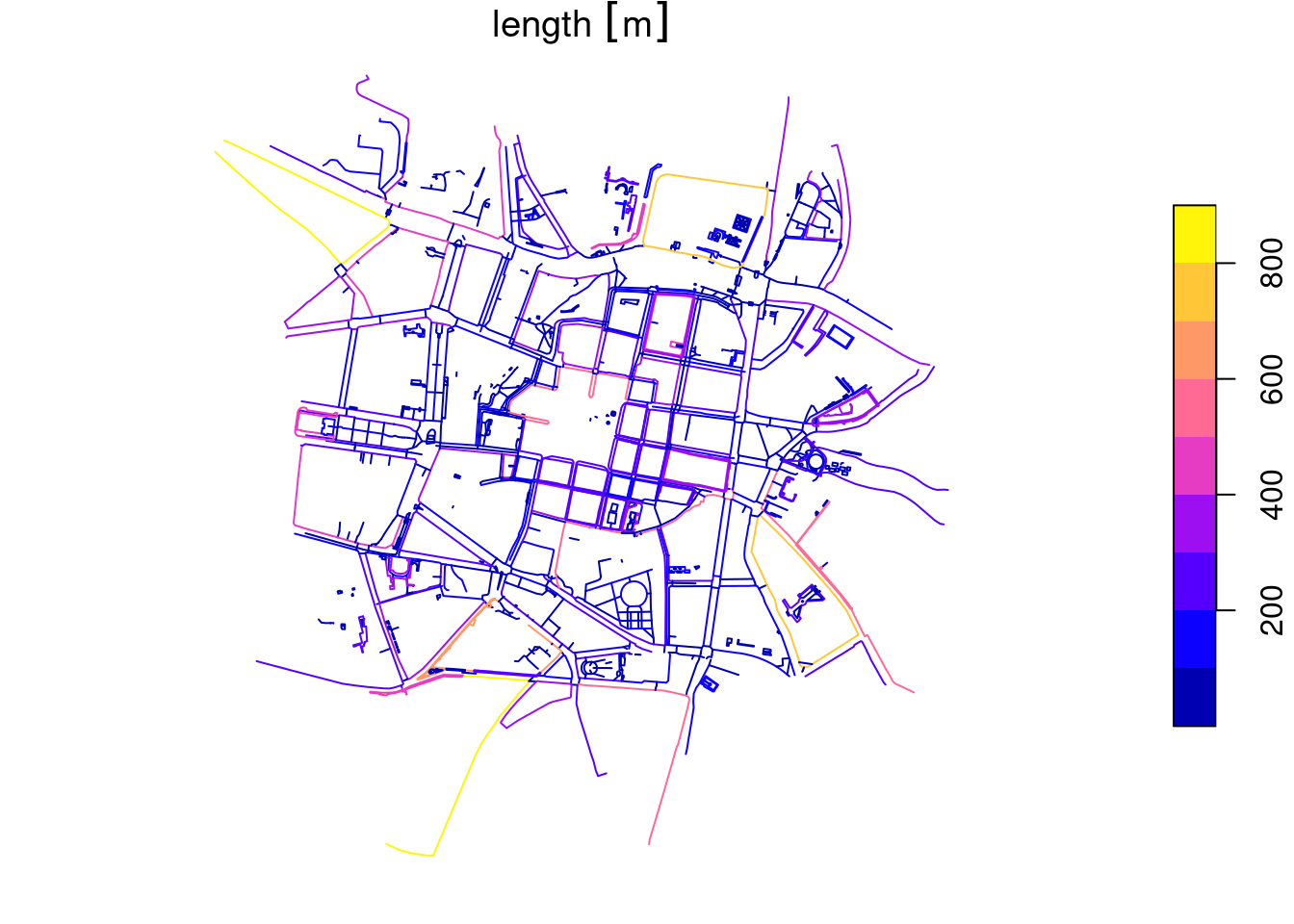
2.2.2 Miara pośrednictwa
Miara pośrednictwa może być także opisana dla krawędzi. W takim przypadku określa ona liczbę najkrótszych ścieżek przechodzących przez krawędź. Miarę pośrednictwa krawędzi oblicza się wykorzystując funkcję tidygraph::centrality_edge_betweenness()
net = net |> activate("edges") |> mutate(betweenness = centrality_edge_betweenness())
edge_sf = st_as_sf(net)
plot(edge_sf["betweenness"])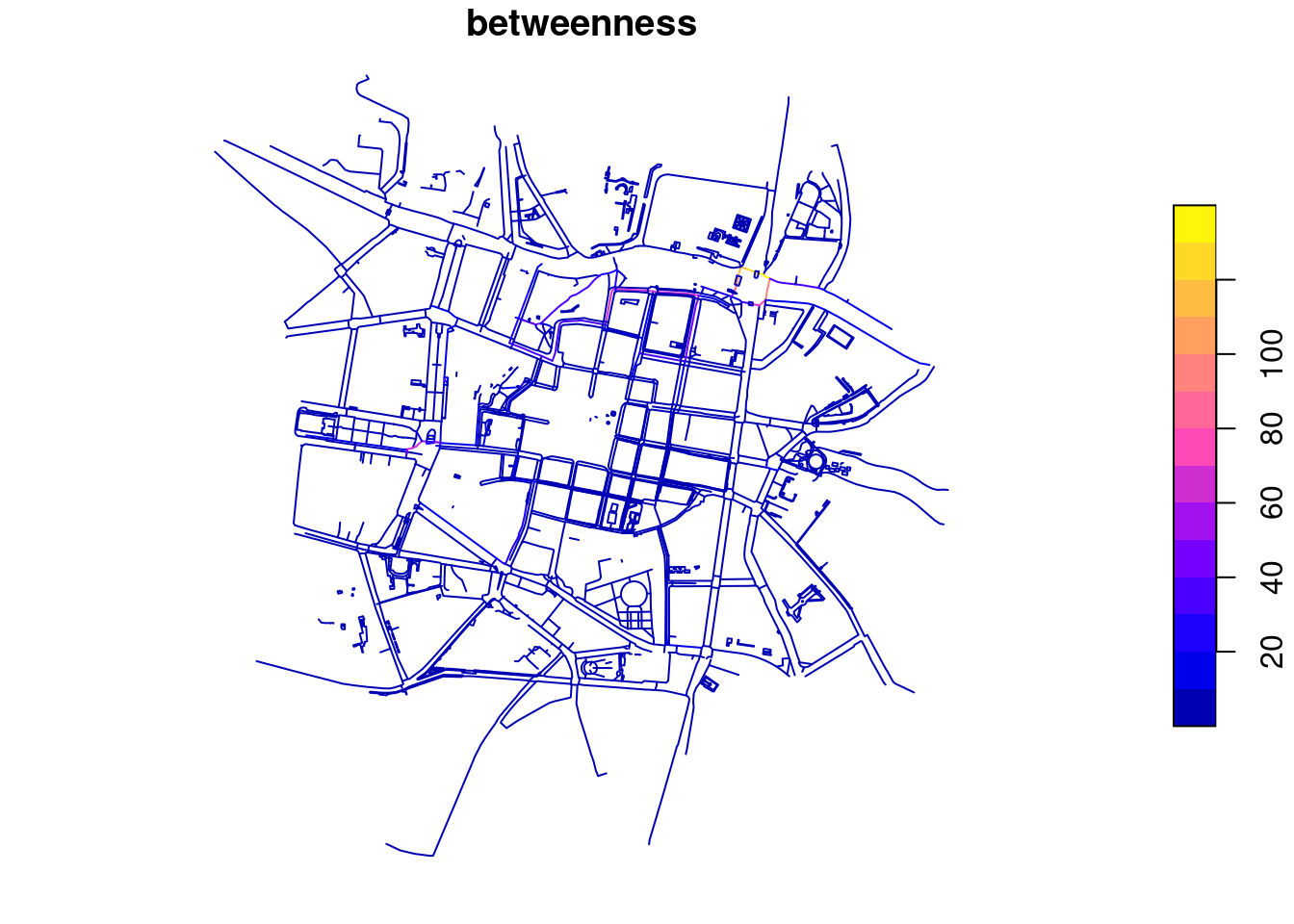
2.3 Miary strukturalne grafu
Miary strukturalne grafu charakteryzują całą sieć.
2.3.1 Średni stopień wiezchołka grafu
Średni stopień wierzchołka grafu obliczany jest jako średnia arytmetyczna stopnia wierzchołka. Poza średnią można obliczyć także inne statystyki opisowe.
summary(nodes_sf$degree) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000 0.0000 1.0000 0.7333 1.0000 3.0000 2.3.2 Gęstość grafu
Gęstość grafu określa, ile powiązań istnieje między wierzchołkami w porównaniu do tego, ile powiązań między wierzchołkami jest możliwych. Gęstość grafu oblicza się wykorzystując funkcję edge_density() z pakietu igraph.
density = igraph::edge_density(net)
density[1] 0.00047616242.3.3 Średnica grafu
Średnica grafu (podawana w liczbie krawędzi) określana jest przez odległość między dwoma najdalej położonymi wierzchołkami (biorąc pod uwagę najkrótszą możliwą drogę między nimi). Średnica grafu obliczana jest używając funkcji graph_diameter() z pakietu igraph.
diameter = with_graph(net, graph_diameter())
diameter[1] 182.3.4 Średnia odległość
Średnia odległość między węzłami w sieci jest obliczana używając funkcji graph_mean_dist().
mean_distance = with_graph(net, graph_mean_dist())
mean_distance[1] 2.7932.4 Współczynnik klasteryzacji
2.4.1 Globalny współczynnik klasteryzacji
Globalny współczynnik klasteryzacji obliczany dla całego grafu informuje w jakim stopniu wierzchołki w grafie mają tendencję do grupowania się. Oblicza się go wykorzystując funkcję igraph::transitivity(G, type = "global").
igraph::transitivity(net, type = "global")[1] 0.0056285182.4.2 Lokalny współczynnik klasteryzacji
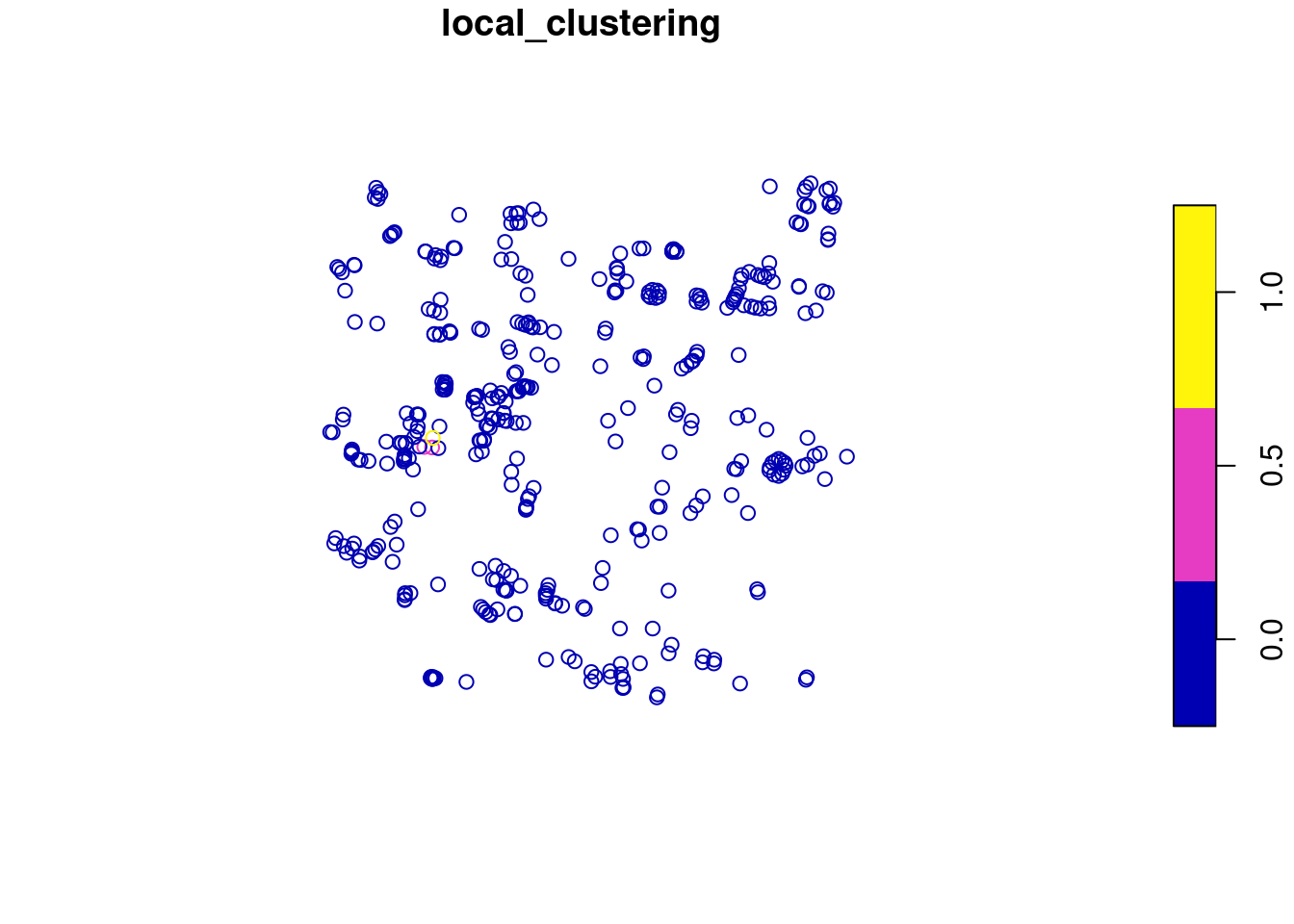
Dla każdego wierzchołka grafu można także obliczyć lokalny współczynnik klasteryzacji, który informuje jaki procent sąsiadów wierzchołka V także ze sobą sąsiaduje.
net = net |> activate("nodes") |> mutate(local_clustering = igraph::transitivity(net, type = "local"))
nodes_sf = st_as_sf(net)plot(nodes_sf["local_clustering"])