Analiza rozkładu przestrzennego danych punktowych

Metody oparte na intensywności

library(spatstat)
library(tmap)

1 Metody oparte na analizie intensywności

W analizie intensywności rozkład przestrzenny punktów jest charakteryzowany względem określonego obszaru badań (np. granica miasta Poznań). Rozkład charakteryzowany jest za pomocą gęstości \(\lambda\) - liczby zdarzeń (\(n\)) na jednostkę powierzchni (\(a\)) obliczanej na podstawie danych.

• intensywność zdarzenia (event) jest stała dla całego obszaru

  • średnia intensywność obliczana jako liczba zdarzeń \(n\) na jednostkę powierzchni \(a\) (\(\lambda = \frac{n}{a}\))

• intensywność zmienia się wraz z lokalizacją

  • test zliczania w kwadratach (ang. quadrat count test)
  • estymacja gęstości jądra (ang. kernel density estimation)

2 Metody oparte na analizie intensywności w R

Obliczenie gęstości wymaga przekształcenia obiektów na typ ppp (plannar point pattern) oraz zdefiniowanie obszaru analizy (tzw. okna, ang. window).

W tym celu zostaną wykorzystane dwie funkcje z pakietu spatstat:

• as.ppp - konwertuje dane na obiekty klasy ppp. Wymaga podania obiektu oraz określenia obszaru analizy.
• as.owin - tworzy okno (window) na podstawie innego obiektu (np. granic miasta Poznania)

Pakiet spatstat dostarcza także funkcji:

• quadratcount() - zliczanie punktów w kwadratach
• quadrat.test() - test zliczania w kwadratach
• density() - analiza gęstości jądra

Ponadto funkcja summary() zastosowana do obiektu klasy ppp dostarcza informacji o średniej intensywności, liczbie puntków oraz powierzchni analizowanego obszaru.

3 Przykład 1: Przestępczość w Poznaniu

W przykładzie 1 wykorzystano dane dotyczące przestępczości w Poznaniu (plik przestepstwa_2019.gpkg) wraz z granicą miasta Poznania (plik pzn_borders.gpkg). Do podsumowania rozkładu przestępczości wykorzystano statystyki centrograficzne. Plik przestepstwa_2019.gpkg zawiera tylko kolumnę geom bez dodatkowych atrybutów.

library(sf)

Linking to GEOS 3.10.2, GDAL 3.4.1, PROJ 8.2.1; sf_use_s2() is TRUE

# dane punktowe
p2019 = read_sf("data/przestepstwa_2019.gpkg")
#granica miasta Poznań
pzn = read_sf("data/pzn_borders.gpkg")

3.1 Analiza intensywności

W analizie intensywności rozkład przestrzenny punktów jest charakteryzowany względem określonego obszaru badań (np. granica miasta Poznań). Rozkład charakteryzowany jest za pomocą gęstości - liczby zdarzeń (\(n\)) na jednostkę powierzchni (\(a\)) obliczanej na podstawie danych.

\[\hat{\lambda} = \frac{n}{a}\]

Obliczenie gęstości wymaga przekształcenia obiektów na typ ppp (plannar point pattern) oraz zdefiniowanie obszaru analizy (tzw. okna, ang. window). Funkcja as.ppp() z pakiety spatstat służy do przekonwertowania danych na obiekty klasy ppp. Wymaga podania obiektu oraz określenia obszaru analizy. Funkcja as.owin() z pakietu spatstat tworzy okno (window) na podstawie innego obiektu (np. granicy miasta Poznania).

library(spatstat)
#przekształcenie obiektu sf na obiekt owin definiujący okno (obszar analizy) dla obiektów ppp
pzn_owin = as.owin(pzn)
#przekształcenie daych punktowych na obiekt ppp. 
p2019_ppp = as.ppp(st_geometry(p2019), W = pzn_owin)

Obiekt p2019_ppp klasy ppp zawiera informację o liczbie punktów położonych w analizowanym obszarze oraz o współrzędnych oganiczających obszar analizy.

p2019_ppp

Planar point pattern: 1661 points
window: polygonal boundary
enclosing rectangle: [345943.2, 368927.8] x [493660, 517878.9] units

Funkcja summary() zastosowana dla obiektu klasy ppp dostarcza dodatkowych informacji, w tym o średniej intensywności (avarage intensity) - tj. liczbie punktów na jednostkę powierzchni oraz powierzchni analizowanego obszaru (window area) w jednostkach układu współrzędnych.

summary(p2019_ppp)

Planar point pattern:  1661 points
Average intensity 6.347623e-06 points per square unit

Coordinates are given to 10 decimal places

Window: polygonal boundary
single connected closed polygon with 3139 vertices
enclosing rectangle: [345943.2, 368927.8] x [493660, 517878.9] units
                     (22980 x 24220 units)
Window area = 261673000 square units
Fraction of frame area: 0.47

Dane dla miasta Poznania są w PUWG1992, w którym jednostki są podane w metrach. Obiekt klasy ppp można dowolnie przeszkalować. Poniżej obiekt zostanie przeskalowany z metrów na km.

p2019_ppp2 = rescale(p2019_ppp, 1000)

summary(p2019_ppp2)

Planar point pattern:  1661 points
Average intensity 6.347623 points per square unit

Coordinates are given to 13 decimal places

Window: polygonal boundary
single connected closed polygon with 3139 vertices
enclosing rectangle: [345.9432, 368.9278] x [493.66, 517.8789] units
                     (22.98 x 24.22 units)
Window area = 261.673 square units
Fraction of frame area: 0.47

Aby uzyskać tylko informację o gęstości punktów można użyć polecenia:

summary(p2019_ppp2)$intensity

[1] 6.347623

Analiza intensywności zależna jest od przyjętego obszaru analizy. Poniżej jako obszar analizy przyjmiemy obwiednię obszaru miasta Poznania (bounding box).

pzn_owin_bb = as.owin(st_bbox(pzn))
p2019_ppp_bb = as.ppp(st_geometry(p2019), W = pzn_owin_bb)
p2019_ppp_bb2 = rescale(p2019_ppp_bb, 1000)
summary(p2019_ppp_bb2)

Planar point pattern:  1661 points
Average intensity 2.983862 points per square unit

Coordinates are given to 13 decimal places

Window: rectangle = [345.9432, 368.9278] x [493.66, 517.8789] units
                    (22.98 x 24.22 units)
Window area = 556.661 square units

Przyjmując jako obszar analizy zasięg warstwy (bounding box) zamiast granicy miasta Poznania średnia intensywność zmienia się z 6,34 (granica Poznania) do 2,98. Poniższa wizualizacja pokazuje zakres granicy Poznania (niebieska linia), zasięgu warstwy (szary poligon) oraz położenia punktów.

library(tmap)

bb = st_as_sfc(st_bbox(pzn))
tm_shape(bb) + 
  tm_borders(fill = "grey") + 
tm_shape(pzn) + 
  tm_borders(col = "blue") + 
tm_shape(p2019) + 
  tm_dots()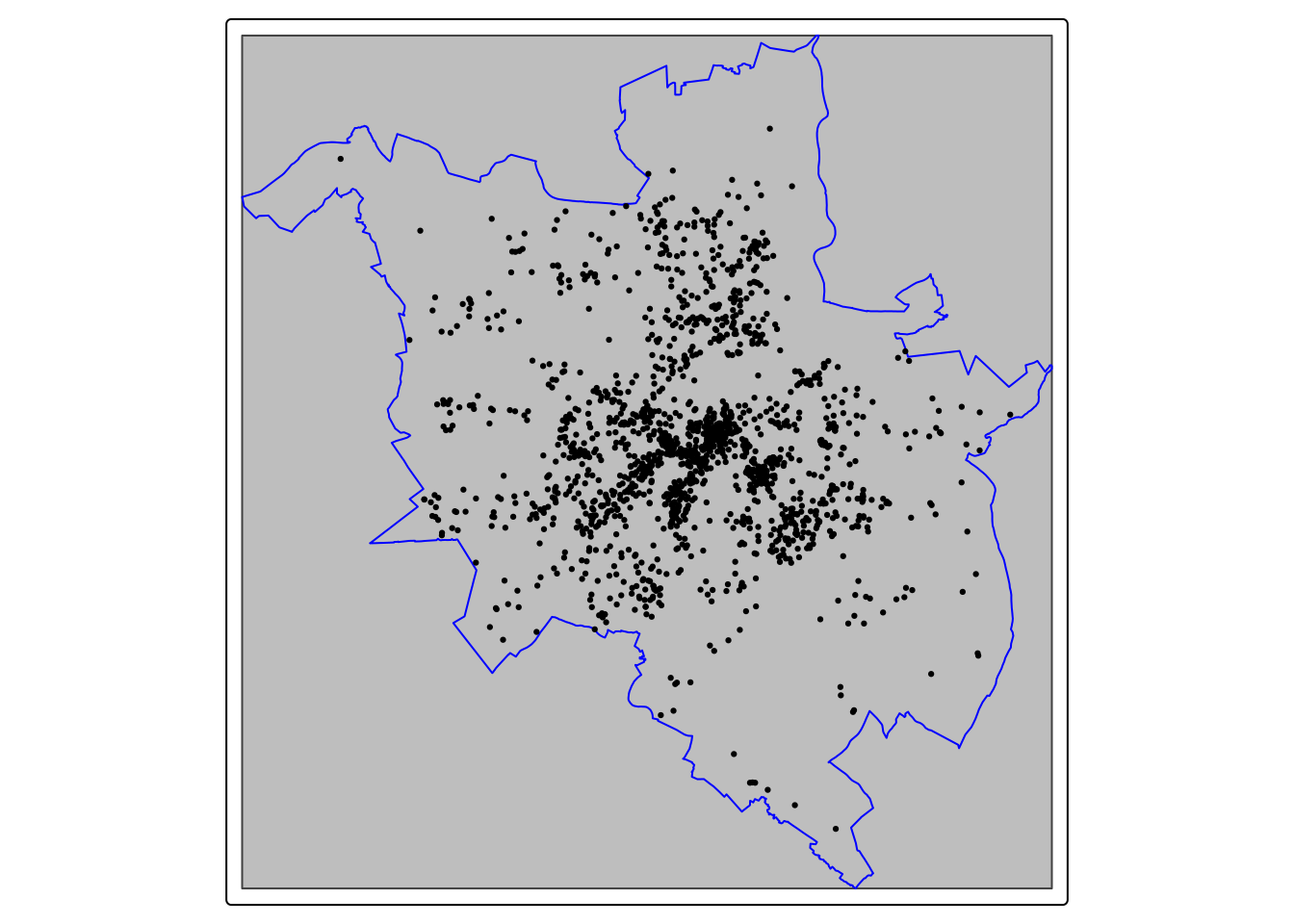

3.2 Zliczenie punktów w siatce

Intensywność punktów może nie być stała dla całego obszaru, a zmieniać się wraz z lokalizacją. Do zliczenia punktów w siatce można użyć funkcji quadratcount() z pakietu spatstat. Wynik można przedstawić numerycznie lub graficznie. Funkcja quadratcount() wymaga podania nazwy obiektu klasy ppp (p2019_pp) oraz liczby komórek w osi x oraz y (parametr nx oraz ny).

p2019_count = quadratcount(p2019_ppp, nx = 4, ny = 4)
plot(quadratcount(p2019_ppp, nx = 4, ny = 4), main = "Liczba przestępstw")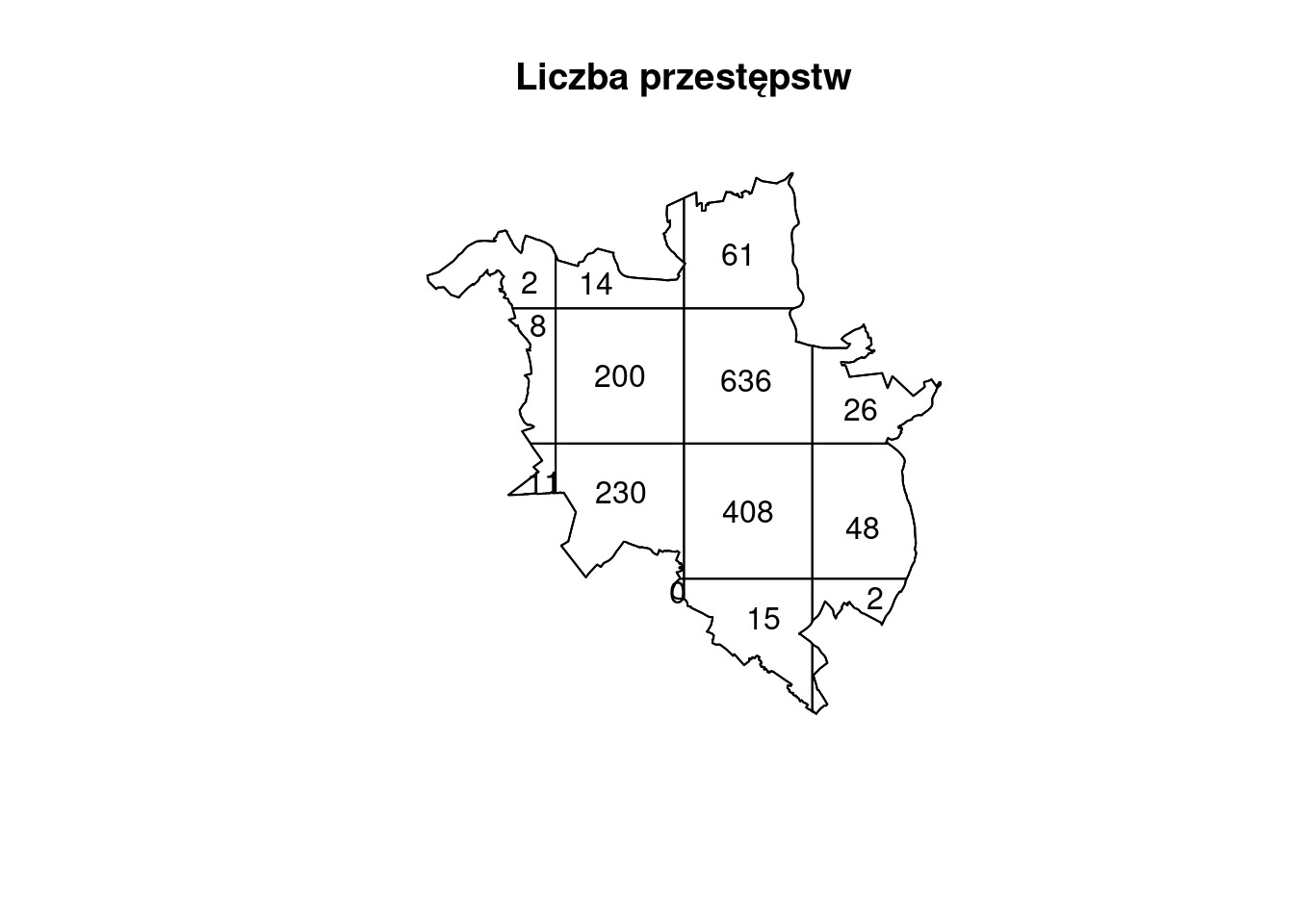

p2019_count

tile
Tile row 1, col 1 Tile row 1, col 2 Tile row 1, col 3 Tile row 2, col 1 
                2                14                61                 8 
Tile row 2, col 2 Tile row 2, col 3 Tile row 2, col 4 Tile row 3, col 1 
              200               636                26                11 
Tile row 3, col 2 Tile row 3, col 3 Tile row 3, col 4 Tile row 4, col 2 
              230               408                48                 0 
Tile row 4, col 3 Tile row 4, col 4 
               15                 2 

Aby otrzymać bardziej zawansowaną wizualizację należy utworzyć siatkę jako obiekt przestrzenny pakietu sf

• Tworzenie siatki - pakiet sf

#utworzenie poligonu o zasiegu warstwy pzn z granicami miasta Poznania
pzn_bb = st_sf(geom = st_as_sfc(st_bbox(pzn)))
#utworzenie siatki, parametr n oznacza liczbę oczek siatki. 
pzn_grid = st_make_grid(pzn_bb, n = 4)
#obiekt przestrzenny zawierający siatkę 
pzn_grid_sf = st_sf(geometry = pzn_grid)

plot(pzn_grid_sf)

• Zliczenie liczby punktów w każdym oczku siatki

Liczba punktów w każdym oczku siatki zostanie obliczona poprzez przecięcie dwóch obiektów przestrzennych: pzn_grid zawierającego siatkę oraz warstwy punktowej p2019. W poniższym poleceniu funkcja st_intersects() przecina dwa obiekty oraz zwraca listę. Każdy element listy to jedno oczko siatki, wartości to numery punktów znajdujące się w danym oczku. Funkcja length() zwraca długość każdego elementu listy.

pzn_grid_sf$dane = lengths(st_intersects(pzn_grid, p2019))

head(pzn_grid_sf$dane, 16)

 [1]   0   0  15   2  11 230 408  48   8 200 636  26   2  14  61   0

library(tmap)
library(viridis)
tm_shape(pzn_grid_sf) + 
    tm_polygons(col = "dane",  palette = "YlGn", n = 4, title = "Liczba punktów") + 
    tm_shape(p2019) + 
    tm_dots() + 
  tm_layout(legend.outside = TRUE)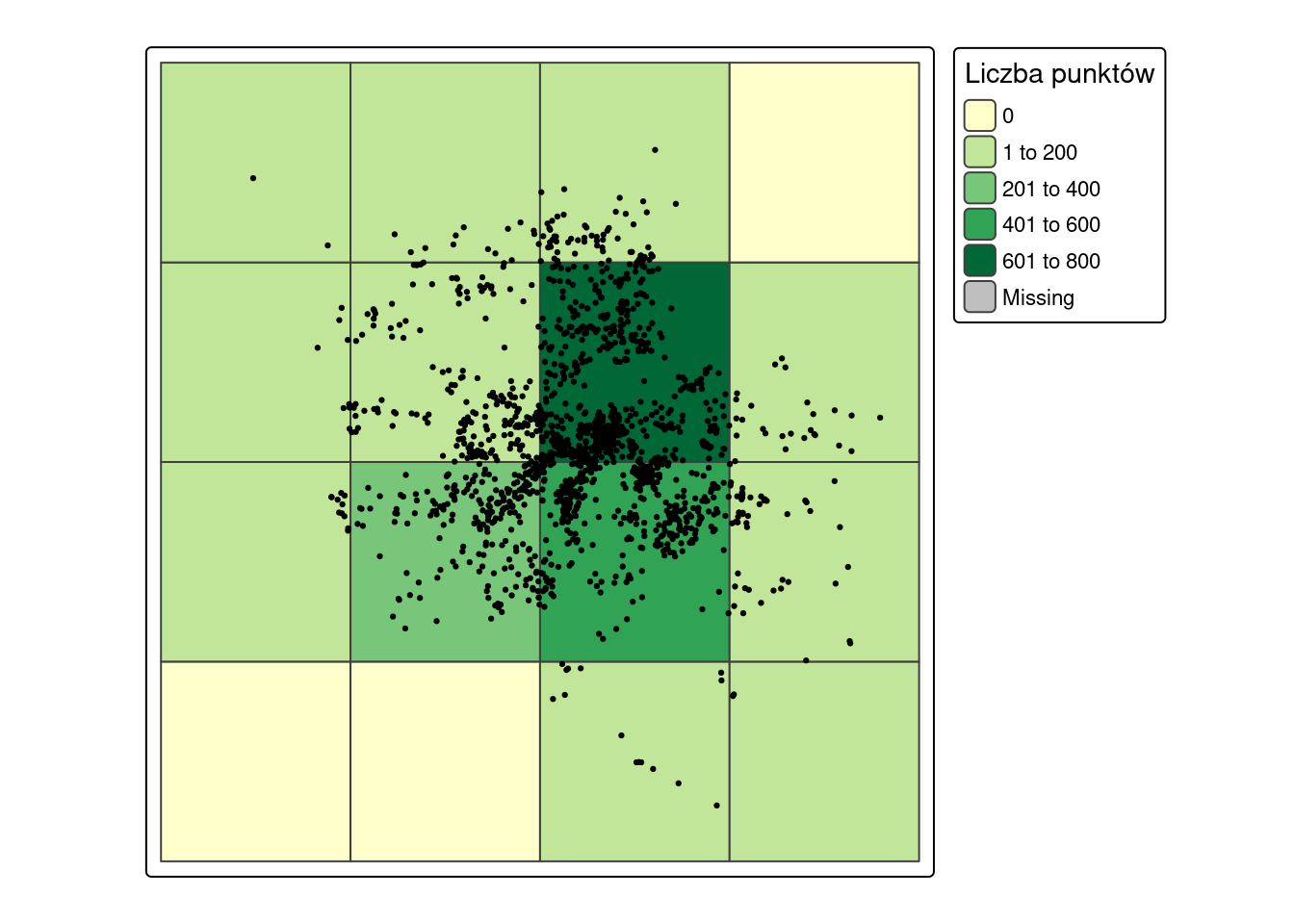

3.3 Test zliczania w kwadratach

Test zliczania w kwadratach służy do testowania hipotezy zerowej zakładającej, że dane są rozmieszczone losowo. Test ten dzieli obszar na równe kwadraty, a następnie zlicza liczbę punktów w każdym kwadracie oraz porównuje z wartościami oczekiwanymi (ta sama liczba punktów w każdym kwadracie). Test zliczenia w kwadratach można wykonać wykorzystując funkcję quadrat.test() z pakietu spatstat. Funkcja wymaga podania nazwy obiektu klasy ppp oraz liczby oczek siatki w osi x oraz y (nx, ny).

quadrat.test(p2019_ppp, nx = 4, ny = 4)

Warning: Some expected counts are small; chi^2 approximation may be inaccurate

    Chi-squared test of CSR using quadrat counts

data:  p2019_ppp
X2 = 1538, df = 13, p-value < 2.2e-16
alternative hypothesis: two.sided

Quadrats: 14 tiles (irregular windows)

Jak zinterpretujemy wynik testu?

qtest = quadrat.test(p2019_ppp, nx = 4, ny = 4)

Warning: Some expected counts are small; chi^2 approximation may be inaccurate

plot(qtest, nx = 4, ny = 4)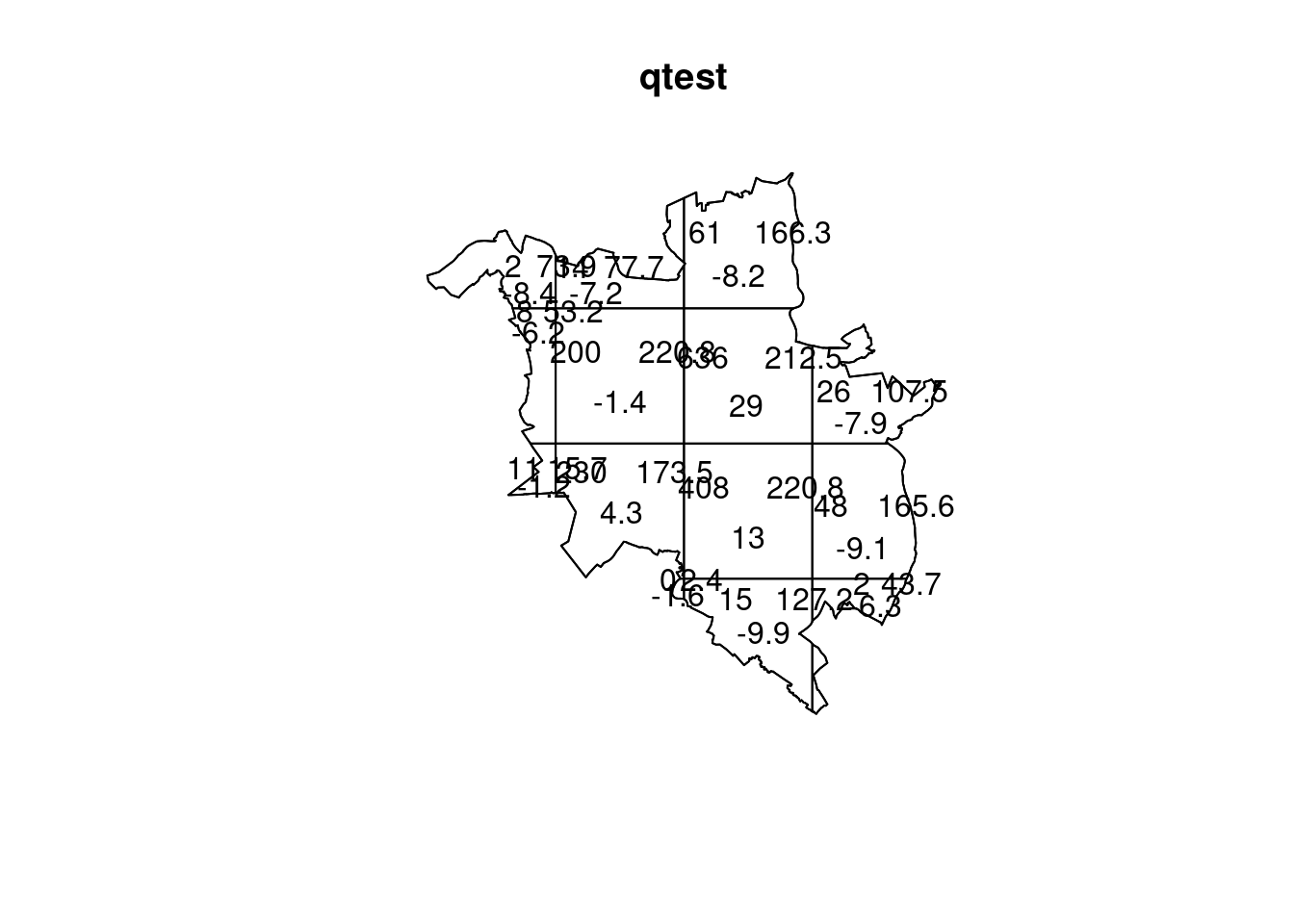

3.4 Analiza gęstości jądra

Test zliczenia w kwadratach oblicza lokalną intensywność poprzez podzielenie obszaru na równej wielkości kwadraty. Analiza gęstości jądra (kernel density estimation) wykorzystuje ruchome okno do obliczenia lokalnej intensywności dla podzbiorów badanego obszaru. Ruchome okno definiuje się poprzez ustawienie parametrów jądra (kernel) - kształtu oraz rozmiaru (bandwith). W wyniku otrzymujemy siatkę rastrową, gdzie każde oczko siatki ma przypisaną wartość intensywności obliczoną dla obszaru o wielkości ruchomego okna wyśrodkowanego dla komórki do której przypisana jest wartość. Rozdzielczość wynikowej komórki będzie zawsze mniejsza niż rozmiar ruchomego okna. Jako jądro (kernel) często wykorzystuje się funkcję gaussowską.

W R analizę gęstości jądra można wykonać używając funkcji density(). W poniższym przykładzie parametr sigma oznacza rozmiar (bandwith). Sigma = 500 oznacza ruchome okno o wielkości 500m.

library(terra)
p2019_density1 = rast(density(p2019_ppp, sigma = 500))
crs(p2019_density1) = crs(pzn)

tm_shape(p2019_density1) + 
    tm_raster(palette = "-viridis", style = "cont") +
    tm_shape(p2019) +
    tm_dots() + 
  tm_layout(legend.outside = TRUE)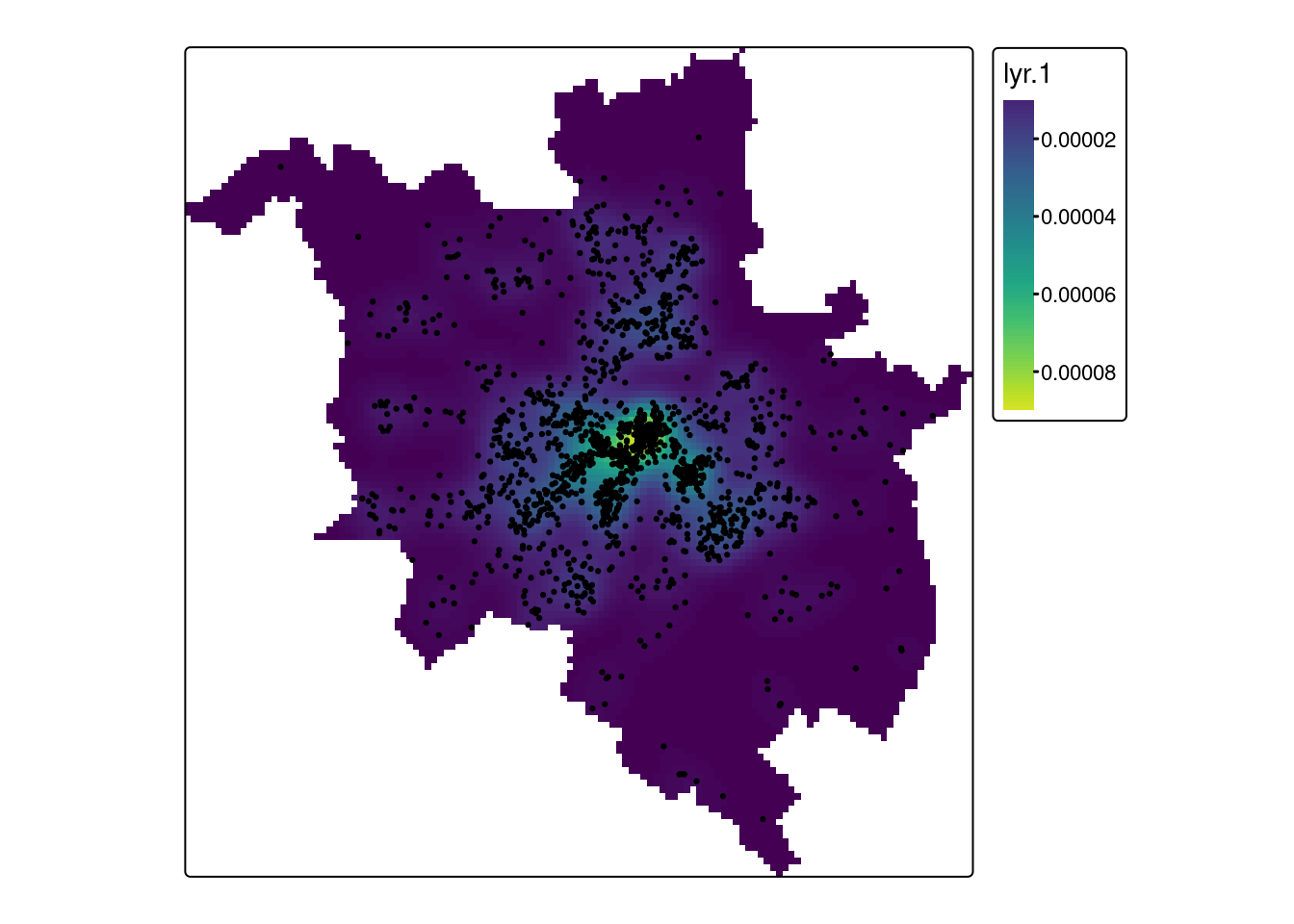

p2019_density2 = rast(density(p2019_ppp, sigma = 1500))
crs(p2019_density2) = crs(pzn)

tm_shape(p2019_density2) + 
    tm_raster(palette = "-viridis", style = "cont") +
    tm_shape(p2019) +
    tm_dots() + 
  tm_layout(legend.outside = TRUE)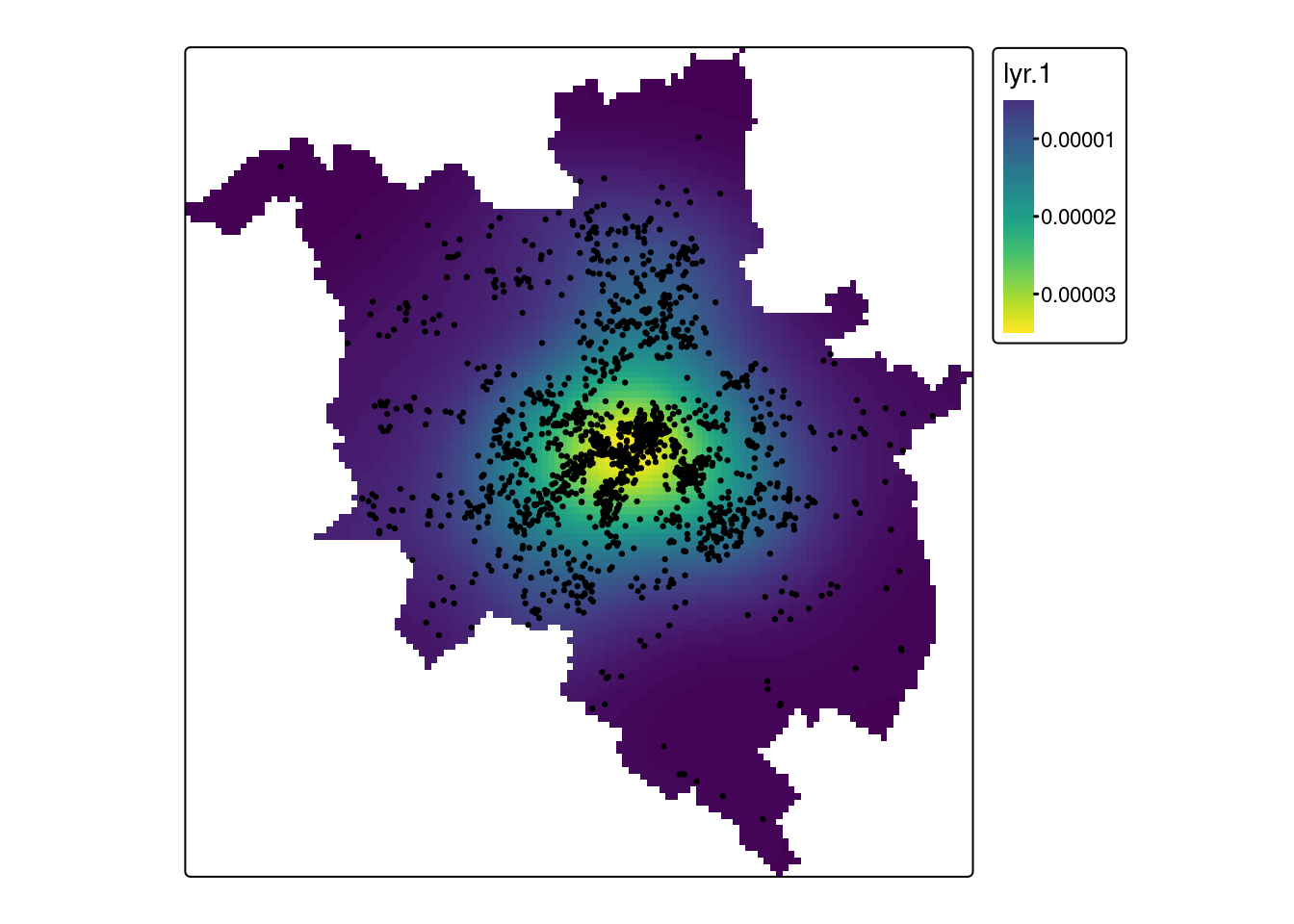

4 Przykład 2: Rozkład przestrzenny szkół w Poznaniu

W poniższym przykładzie przeanalizowano przestrzenny rozkład szkół podstawowych w Poznaniu wykorzystując metody oparte na intensywnści:

• Analizę średniej intensywności
• Test zliczania w kwadratach
• Analizę gęstości jąda

library(sf)
library(spatstat)
#wczytanie danych przestrzennych. Granica jest wykorzystywana wyłącznie do wizualizacji danych. 
szkoly = read_sf("data/out_poznan_szkoly.gpkg", layer = "szkoly")
pzn = read_sf("data/out_poznan_szkoly.gpkg", layer = "granica")

#konwersja do obiektu klasy ppp 
pzn_owin = as.owin(pzn)
szkoly_ppp = as.ppp(szkoly, w = pzn_owin)

4.1 Analiza intensywności

summary(szkoly_ppp)

Planar point pattern:  84 points
Average intensity 5.274679e-07 points per square unit

Coordinates are given to 10 decimal places

Window: rectangle = [351938.9, 365782.3] x [500644.3, 512148] units
                    (13840 x 11500 units)
Window area = 159251000 square units

4.2 Zliczenie punktów w siatce

qc = quadratcount(szkoly_ppp, nx = 4, ny = 4)
plot(qc)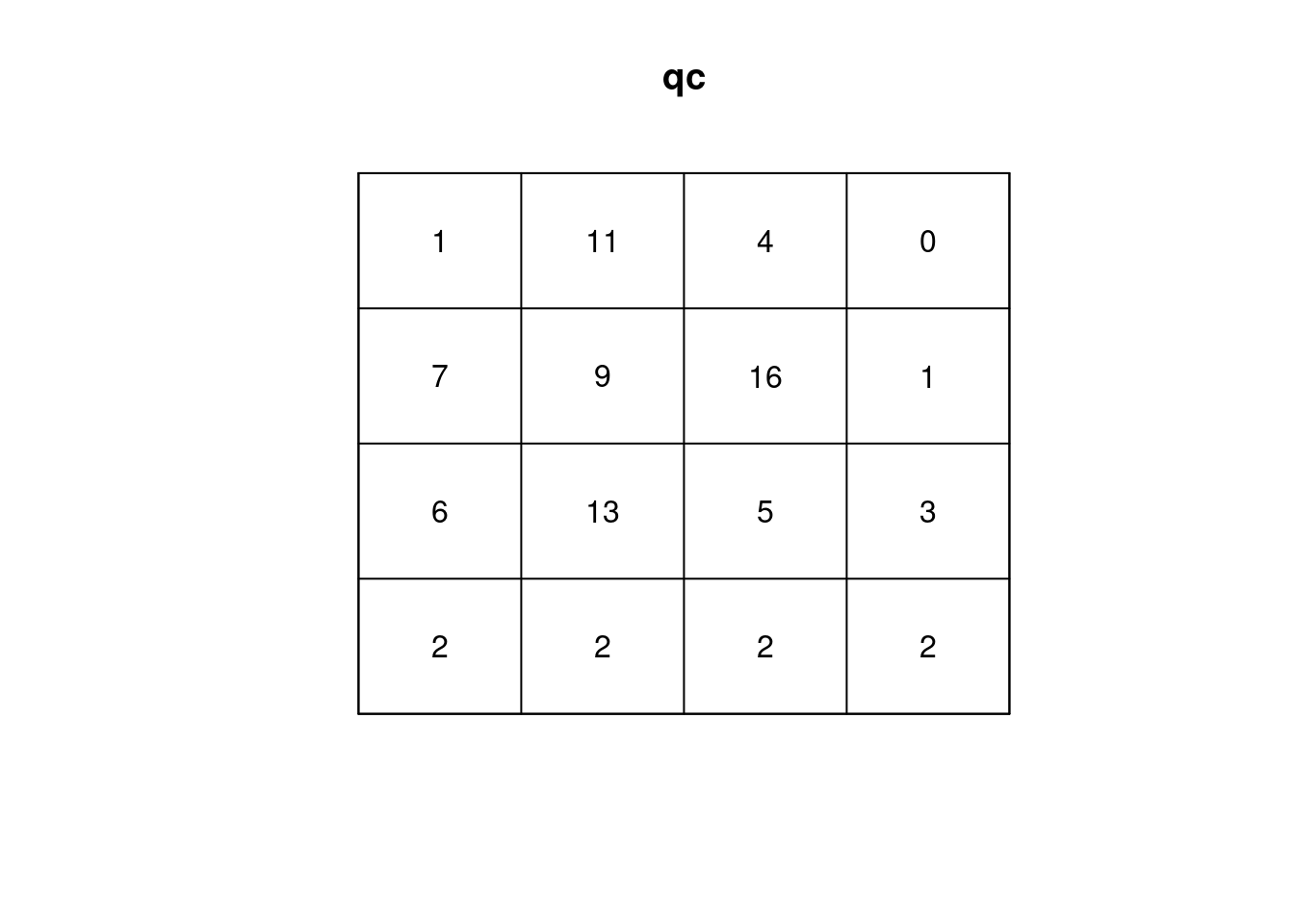

4.3 Test zliczania w kwadratach

quadrat.test(szkoly_ppp, nx = 4, ny = 4)

    Chi-squared test of CSR using quadrat counts

data:  szkoly_ppp
X2 = 64.571, df = 15, p-value = 8.123e-08
alternative hypothesis: two.sided

Quadrats: 4 by 4 grid of tiles

Jak zinterpetujesz wynik testu?

plot(quadrat.test(szkoly_ppp, nx = 4, ny = 4))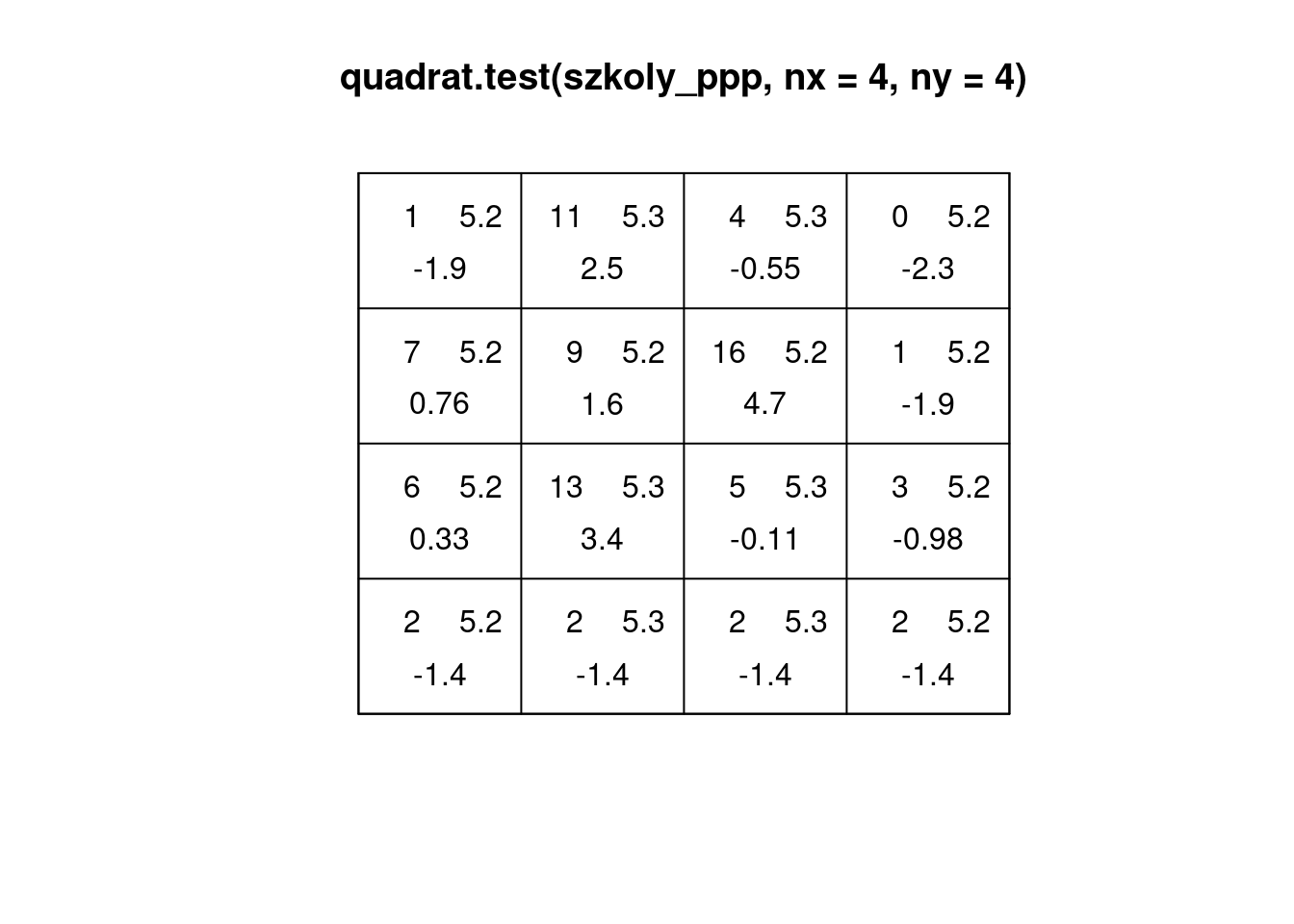

quadrat.test(szkoly_ppp, nx = 2, ny = 2)

    Chi-squared test of CSR using quadrat counts

data:  szkoly_ppp
X2 = 6.381, df = 3, p-value = 0.189
alternative hypothesis: two.sided

Quadrats: 2 by 2 grid of tiles

Jak zinterpetujesz wynik testu dla obszaru podzielonego na 2 kwadraty?

plot(quadrat.test(szkoly_ppp, nx = 2, ny = 2))

4.4 Analiza gęstości jądra

kde12<- density(szkoly_ppp, sigma = 1200)
kde12 <- rast(kde12)
tm_kde12 = tm_shape(kde12) + 
  tm_raster(palette = "-viridis", style = "cont", title = "Bandwidth = 1.2km")

kde05 <- density(szkoly_ppp, sigma = 500)
kde05 <- rast(kde05)
tm_kde05 = tm_shape(kde05) + 
  tm_raster(palette = "-viridis", style = "cont", title = "Bandwidth = 0.5km")

tmap_arrange(tm_kde12, tm_kde05)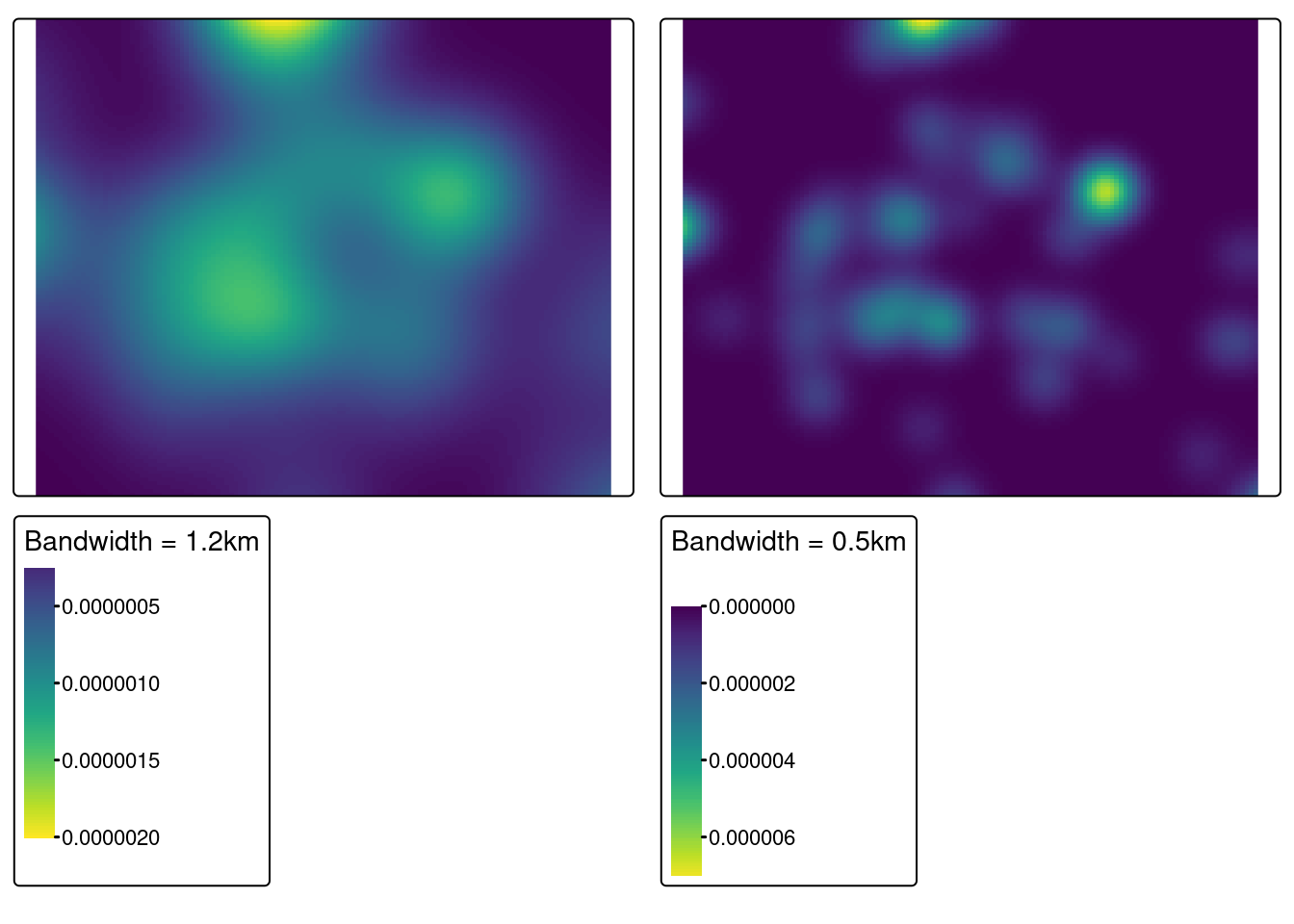

Zinterpretuj wyniki analizy z wykorzystaniem metod opartych o intensywności. Jaki jest rozkład szkół podstawowych w Poznaniu?