Analiza rozkładu przestrzennego danych punktowych

Metody oparte na odległości

Author

Anna Dmowska, Jakub Nowosad

library(spatstat)
library(sf)

1 Metody oparte na odległości

Metody oparte na odległości wykorzystują informację o odległości między każdą lokalizacją pomiaru/obserwacji, a najbliższym innym pomiarem/obserwacją.

1.1 Statystyki najbliższego sąsiada

Statystyki najbliższego sąsiada wykorzystywane są do określenia rozkładu odległości pomiędzy każdą lokalizacją pomiaru/obserwacji, a najbliższym innym pomiarem/obserwacją.

1.2 Wskaźnik Clarka-Evansa

Wskaźnik Clarka-Evansa (1954) określa stosunek między rzeczywistą średnią odległością od najbliższego sąsiada, a oczekiwaną dla rozkładu losowego.

Wartości niższe od 1 wskazują na występowanie skupień punktów
Wartość równa 1 wskazuje na losowy rozkład punktów
Wartości wyższe od 1 wskazują na bardziej regularny ich rozkład (np., dla regularnej siatki heksagonalnej wartość wskaźnika wynosi 2,15)

1.3 Funkcje podsumowujące G, K Ripley’a

funkcja G - podsumowuje rozkład odległości do najbliższego sąsiada w postaci dystrybuanty, wykorzystywana do porównania odległości teoretycznych wynikających z losowego rozkładu punktów z odległościami empirycznymi obliczonymi na podstawie danych.
funkcja K Ripley’a - wykorzystywana do porównania odległości teoretycznych wynikających z losowego rozkładu punktów z odległościami empirycznymi obliczonymi na podstawie danych.

2 Metody oparte na odległości w R

Pakiet spatstat() dostarcza kilku funkcji pozwalających na wykorzystanie metod opartych na odległości do analizy rozkładu przestrzennego punktów.

pairdist() - zwraca macierz z odległościami między wszystkimi parami punktów w zbiorze danych
nndist() - zwraca wektor odległości od punktu do najbliżego sąsiada; odległości te są uzyskiwane przez sortowanie odległości między parami punktów i wybierana jest minimalna wartości dla każdego punktu
distmap() - oblicza odległość od każdej komórki do najbliższego punktu i zwraca mapę rastrową.
clarkevans() - obliczenie wskaźnika Clarka-Evansa
Gest() - obliczenie funkcji G
Kest() - obliczenie funkcji K
envelope() - estowania hipotezy zerowej dla funkcji G, K

Wykorzystanie funkcji z pakietu spatstat wymaga najpierw przekształcenia danych do obiektu klasy ppp (plannar point pattern).

funkcja ppp() jest używana do tworzenia obiektu punktowego klasy ppp na podstawie ramki danych zawierającej współrzędne x oraz y.
funkcja as.ppp() pozwala na przekształcenie obiektu przestrzennego do klasy ppp

3 Przykład 1: Przestępczość w Poznaniu

W przykładzie 1 wykorzystano dane dotyczące przestępczości w Poznaniu (plik przestepstwa_2019.gpkg) wraz z granicą miasta Poznania (plik pzn_borders.gpkg). Do podsumowania rozkładu przestępczości wykorzystano statystyki centrograficzne. Plik przestepstwa_2019.gpkg zawiera tylko kolumnę geom bez dodatkowych atrybutów.

library(sf)
# dane punktowe
p2019 = read_sf("data/przestepstwa_2019.gpkg")
#granica miasta Poznań
pzn = read_sf("data/pzn_borders.gpkg")

library(tmap)
tm_shape(pzn) + 
    tm_borders() +
    tm_shape(p2019) +
    tm_dots()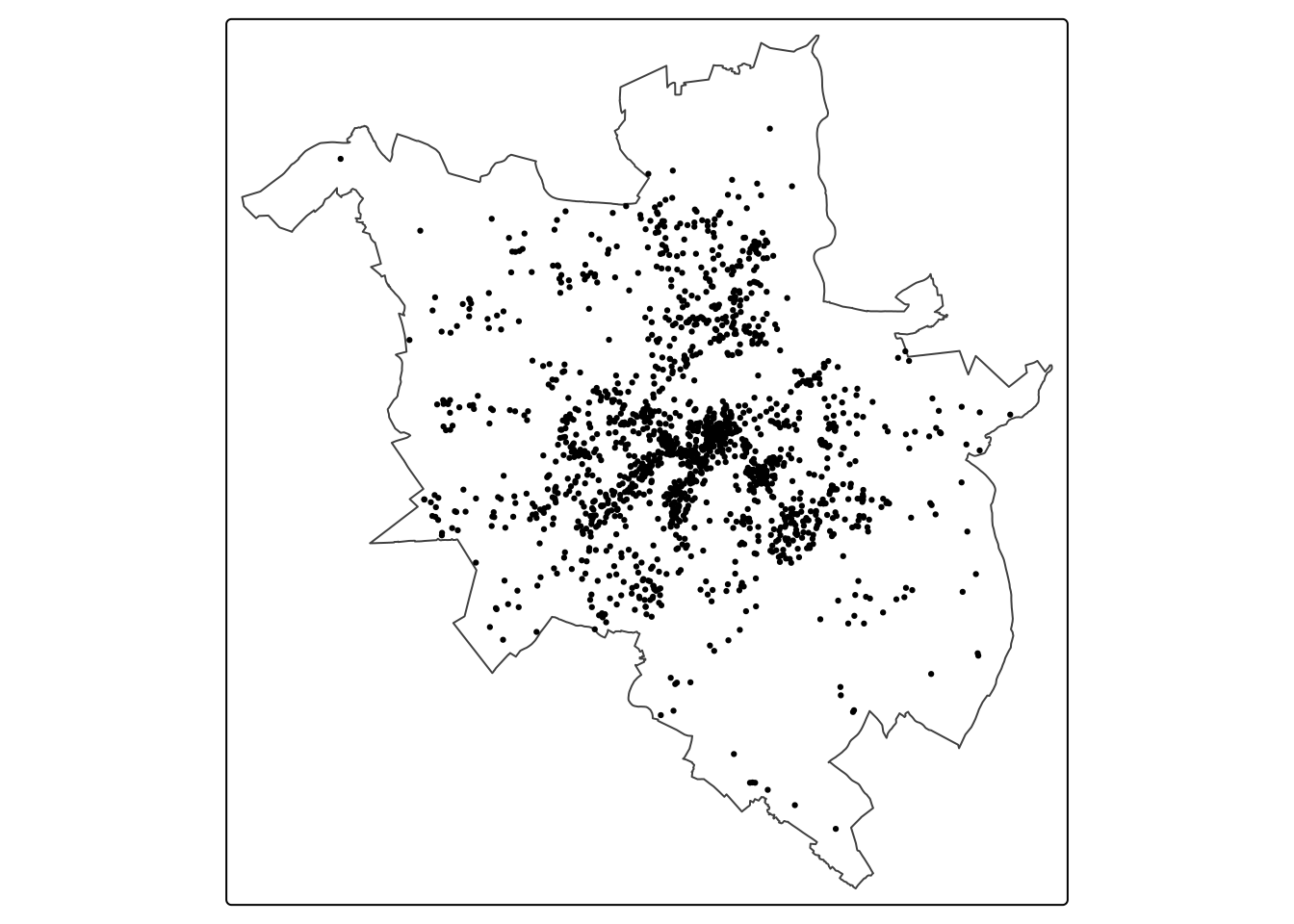

Wykorzystanie funkcji z pakietu spatstat wymaga najpierw przekształcenia danych do obiektu klasy ppp. W tym celu wykorzystuje się funkcję as.ppp(), która pozwala na przekształcenie obiektu przestrzennego do klasy ppp.

library(spatstat)
p2019_ppp = as.ppp(st_geometry(p2019))

3.1 Statystyki najbliższego sąsiada

3.1.1 Obliczenie odległości między punktami

Wyliczenie statystyk najbliższego sąsiada wymaga obliczenia odległości między punktami. Pakiet spatstat dostarcza 3 funkcje do obliczania odległości euklidesowych:

pairdist(): zwraca macierz z odległościami między wszystkimi parami punktów w zbiorze danych.

p2019_pair = pairdist(p2019_ppp)
p2019_pair[1:5, 1:5]

          [,1]      [,2]     [,3]     [,4]      [,5]
[1,]    0.0000  345.3003 2862.262 8306.265  412.9845
[2,]  345.3003    0.0000 2857.224 8607.106  389.4981
[3,] 2862.2616 2857.2245    0.000 7522.023 3215.6132
[4,] 8306.2651 8607.1061 7522.023    0.000 8662.6305
[5,]  412.9845  389.4981 3215.613 8662.631    0.0000

W macierzy wyznaczonej za pomocą funkcji pairdist() pierwszy wiersz zawiera odległości między punktem id = 1 a wszystkimi innymi. Jeśli posortujemy te wartości otrzymamy ciąg od 0 (odległość między punktem 1 i 1 jest równa 0). Druga wartość w tym posortowanym wektorze to odległość do najbliższego sąsiada.

sort(p2019_pair[1,])[1:5]

[1]   0.00000  42.45441  59.10611  73.24603 137.13290

nndist(): zwraca wektor odległości od punktu do najbliżego sąsiada; odległości te są uzyskiwane przez sortowanie odległości między parami punktów i wybierana jest minimalna wartości dla każdego punktu

p2019_nn1 = nndist(p2019_ppp)
p2019_nn1[1:5]

[1]  42.45441  32.89107  69.73521  56.48927 243.91727

Wektor ten można następnie podsumować za pomocą statystyk opisowych otrzymując wartości statystyk najbliższego sąsiada.

distmap() - oblicza odległość od każdej komórki do najbliższego punktu i zwraca mapę rastrową.

plot(distmap(p2019_ppp))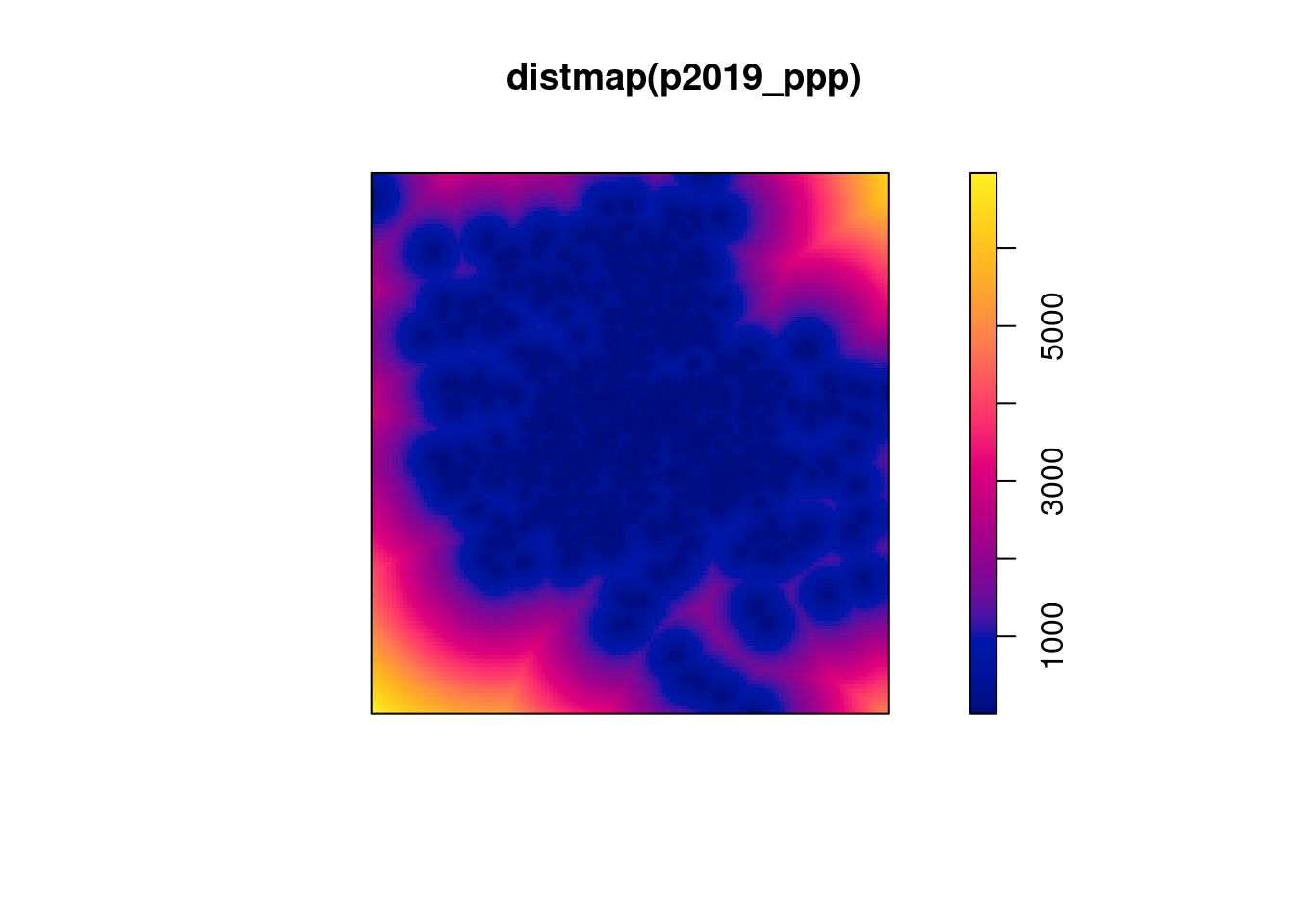

3.1.2 Analiza statystyk najbliższego sąsiada

Funkcja nndist() dla każdego punktu zwraca odległość do najbliższego punktu - sąsiada. Na tej podstawie możemy obliczyć statystyki opisowe oraz przeanalizować jak rozkładają się te odległości w analizowanym zbiorze danych.

p2019_nn1 = nndist(p2019_ppp)
#przekształcenie na ramkę danych jest potrzebne do wizualizacji wyników z wykorzystaniem pakietu ggplot2
p2019_nn1_df = data.frame(shortest_distance = p2019_nn1)
head(p2019_nn1_df)

  shortest_distance
1          42.45441
2          32.89107
3          69.73521
4          56.48927
5         243.91727
6         178.30293

summary(p2019_nn1)

    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
   2.669   42.324   78.596  122.883  148.820 3045.719

round(quantile(p2019_nn1, probs = seq(0, 1, 0.1)), 2)

     0%     10%     20%     30%     40%     50%     60%     70%     80%     90% 
   2.67   22.39   35.75   47.97   63.84   78.60  100.06  128.50  171.23  250.91 
   100% 
3045.72

Podsumowanie wyników dotyczących statystyk najbliższego sąsiada

50% punktów znajduje się w odległości mniejszej lub równiej ok. 79 m od najbliższej próbki
90% punktów w odległości mniejszej lub równiej ok. 251 m od najbliższej próbki

Odległości między najbliższymi punktami:

Minimalna: 3 m
Maksymalna: 3046 m
Średnia: 123 m

Rozkład wartości odległości można także przeanalizować za pomocą histogramu.

library(ggplot2)
ggplot(p2019_nn1_df, aes(x = shortest_distance)) + 
  geom_histogram(binwidth = 100) + 
  labs(x = "Odległość do najbliższego sąsiada [m]") + 
  theme_bw()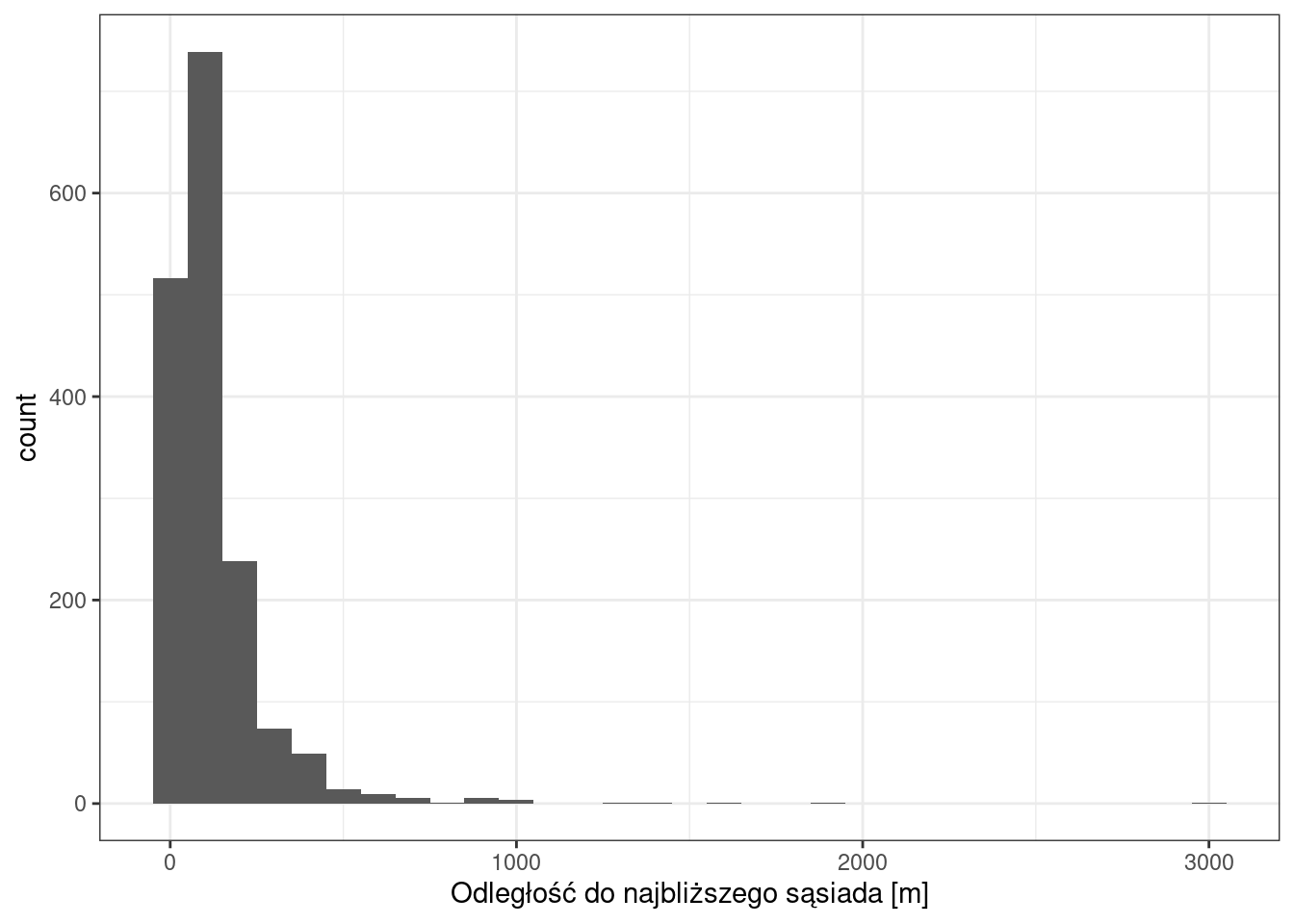

Odległości do najbliższego sąsiada można także przedstawić w postaci dystrybuanty (CDF, cumulative distribution function). Na osi x przedstawiona jest odległość, a na osi y procentowy udział punktów w zbiorze danych. Z wykresu można odczytać, jaki procent punktów ma najbliższego sąsiada w odległości mniejszej lub równej podanej wartości.

# cumulative distribution funcion 
## stat_ecdf - oblicza cdf (cumulative distribution funcion)
ggplot(p2019_nn1_df, aes(shortest_distance)) + 
  stat_ecdf(aes(ymin = 0, ymax = after_stat(y)), geom = "ribbon", fill = "grey95")+
  stat_ecdf() +
  labs(x = "Odległość do najbliższego sąsiada (m)",
       y = "Udział punktów w zbiorze danyh (%)") +
  scale_y_continuous(labels = scales::percent) + 
  theme_bw()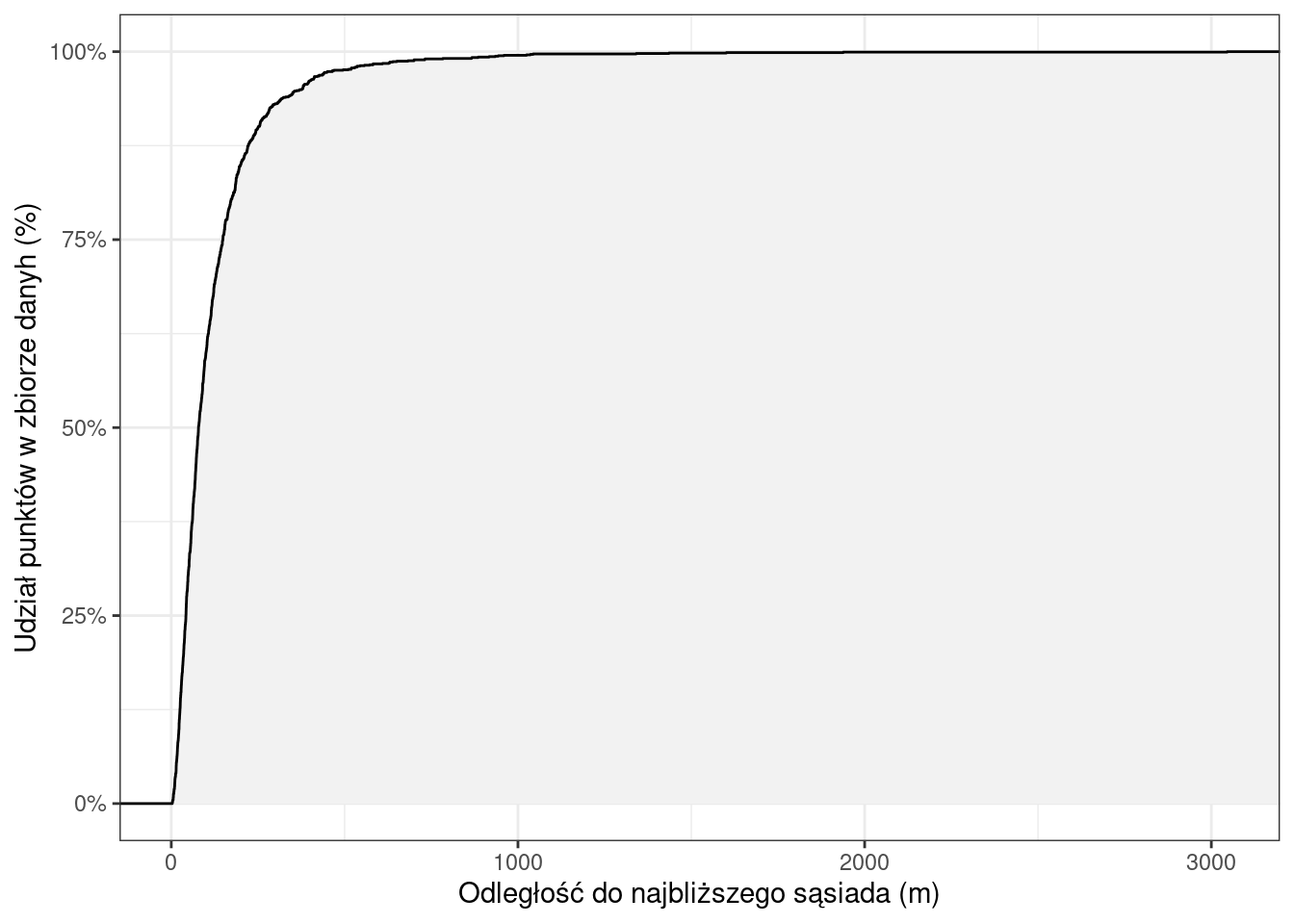

3.2 Funkcje podsumowujące G oraz K Ripley’a

3.2.1 Funkcja G

Funkcje G podsumowuje rozkład odległości do najbliższego sąsiada w postaci dystrybuanty (CDF, cumulative distribution function). Wykorzystywana jest do porównania odległości teoretycznych (\(G_t\)) wynikających z losowego rozkładu punktów z odległościami empirycznymi (\(G_{emp}\)) obliczonymi na podstawie danych.

Funkcja G obliczana jest z wykorzystaniem funkcji Gest() z pakietu spatstat. Wykres pokazuje empiryczną funkcję G (\(\hat{G}_{raw}\)) obliczoną na podstawie danych (czarna linia) oraz teoretyczną wygenerowaną na podstawie rozkładu Poissona (\(G_{pois}\), odpowiadająca losowemu rozkładowi punktów, czerwona przerywana linia).

\(\hat{G}_{raw} > G_{pois}\) - punkty zlokalizowane bliżej niż to wynika z rozkładu losowego (może wskazywać na istnienie klastrów)
\(\hat{G}_{raw} < G_{pois}\) - punkty zlokalizowane dalej niż to wynika z rozkładu losowego (może wskazywać na rozkład regularny lub rozproszony)

p2019_g = Gest(p2019_ppp, correction = "none")
plot(p2019_g)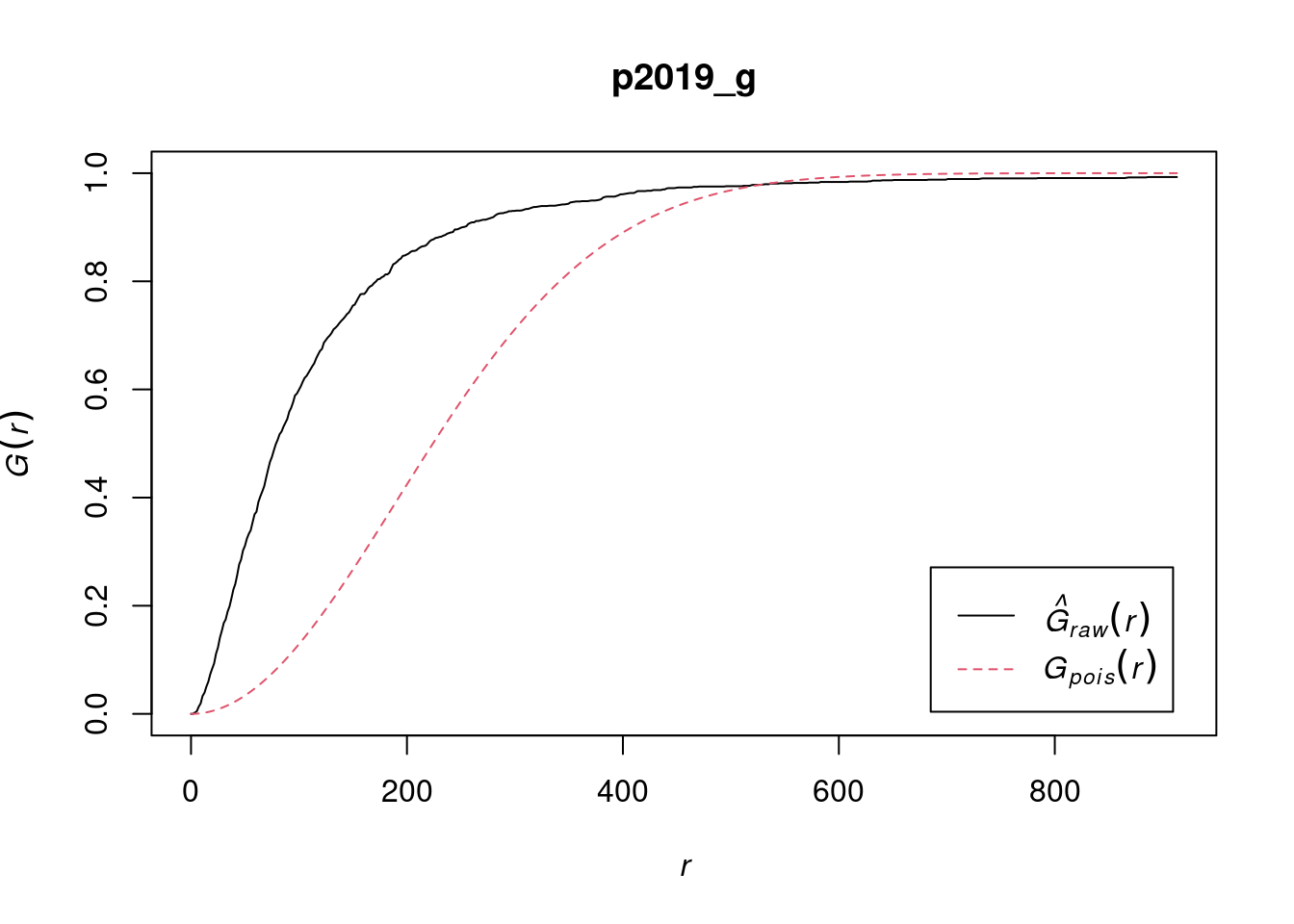

W przykładzie funkcja empiryczna (\(\hat{G}_{raw}\)) przyjmuje wyższe wartości niż funkcja teoretyczna (czarna linia znajduje się powyżej czerwonej) - wskazuje to, że punkty zlokalizowane są bliżej siebie niż to wynika z rozkładu losowego (może wskazywać na istnienie klastrów w danych).

3.2.2 Funkcja K Ripley’a

Funkcja K Ripley’a wykorzystywana jest do porównania odległości teoretycznych wynikających z losowego rozkładu punktów z odległościami empirycznymi obliczonymi na podstawie danych. Funkcja K Ripley’a obliczana jest z wykorzystaniem funkcji Kest() z pakietu spatstat. Wykres pokazuje empiryczną funkcję K Ripley’a (\(\hat{K}_{un}\)) obliczoną na podstawie danych (czarna linia) oraz teoretyczną wygenerowaną na podstawie rozkładu Poissona (\(K_{pois}\); odpowiadająca losowemu rozkładowi punktów). \(\hat{K}_{un} < K_{pois}\) wskazuje na rozrzut punktów, punkty są otoczone przez mniejszą liczbę punktów niż można by oczekiwać w porównaniu do rozkładu losowego.

W poniższym przykładzie funkcja empiryczna (\(\hat{K}_{un}\)) przyjmuje wyższe wartości niż funkcja teoretyczna (czarna linia znajduje się powyżej czerwonej) - wskazuje to, że punkty zlokalizowane są bliżej siebie niż to wynika z rozkładu losowego (może wskazywać na istnienie klastrów w danych).

p2019_k = Kest(p2019_ppp, correction = "none")
plot(p2019_k)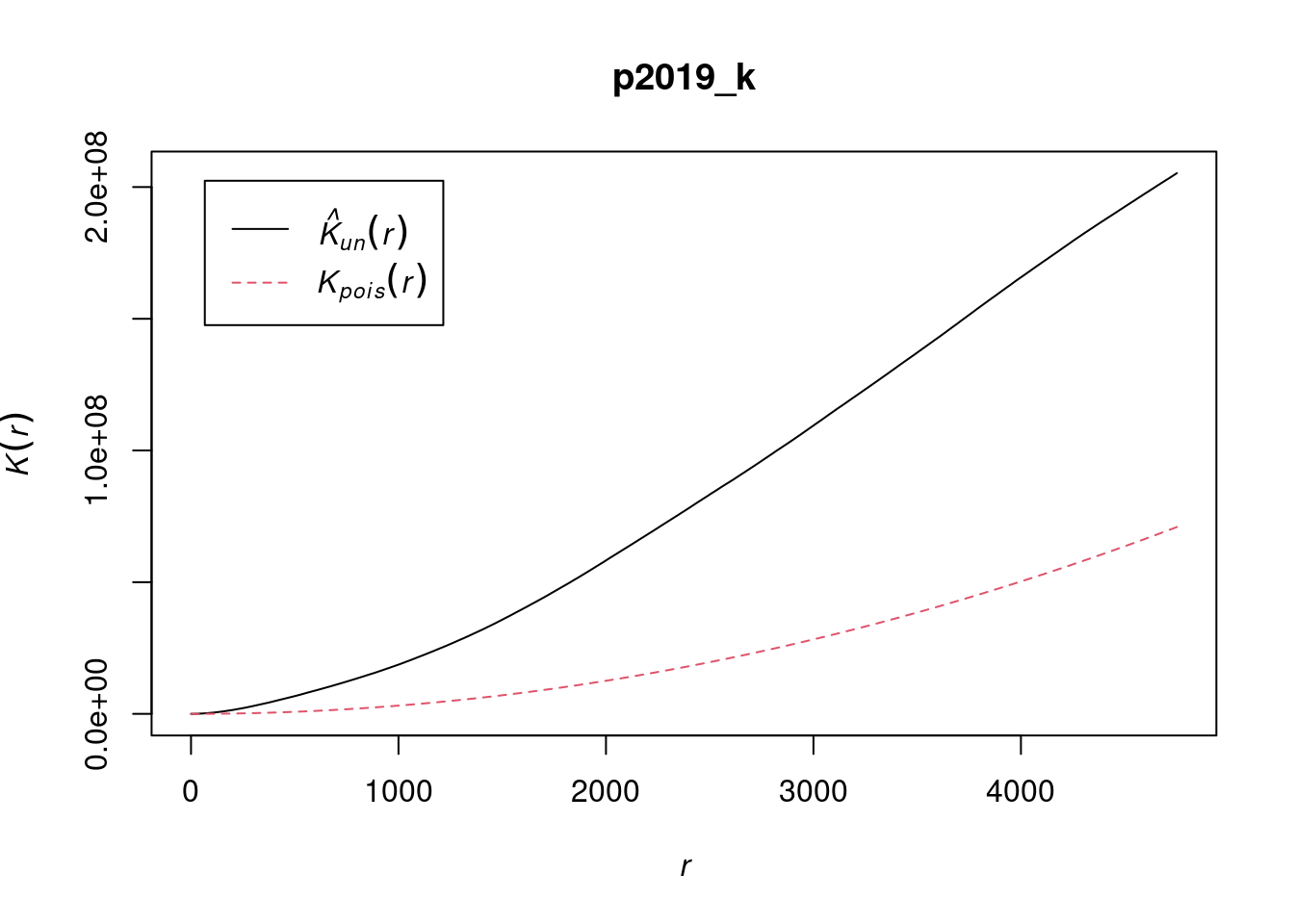

3.2.3 Testowanie istotności hipotezy dotyczącej rozkładu

W przypadku przestrzennej analizy rozkładów punktów istotne jest przetestowanie hipotezy dotyczącej rozkładu danych.

Hipoteza zerowa zakłada, że zdarzenia są rozłożone losowo - tj. wykazują przestrzenną przypadkowość (spatial randomeness -> absence of pattern).
Odrzucenie hipotezy zerowej wskazuje na istnienie jakiś struktur/wzroców przestrzennych (np. skupienia punktów).

Dla funkcji G oraz K Ripley’a nie ma formalnego schematu testowania. Wykorzystuje się w tym celu obwiednię (ang. envelope). Stosując symulacje konstruuje się obszar “nieodrzucania hipotezy zerowej”, a następnie sprawdza się czy krzywa empiryczna mieści się w tym przedziale (nazywanym obwiednią). Jeśli krzywa empiryczna znajduje się poza obwiednią, oznacza to, że dane nie wykazują rozkładu losowego.

Funkcja envelope() z pakietu spatstat tworzy obwiednie dla funkcji G oraz K Ripley’a. Funkcja ta wymaga zdefiniowania:

obiektu klasy ppp (w przykładzie p2019_ppp);
funkcji dla której ma być wyznaczona obwiednia (np. Gest);
liczby symulacji nsim (domyślnie 99);
dodatkowych argumentów funkcji.

W poniższym przykładzie krzywa empiryczna (czarna linia) znajduje się poza zakresem obwiedni (szary kolor), zatem odrzucamy hipotezę o rozkładzie losowym.

p2019_env2 = envelope(p2019_ppp, Gest, nsim = 99, 
                      funargs = list(correction = "none"))
plot(p2019_env2)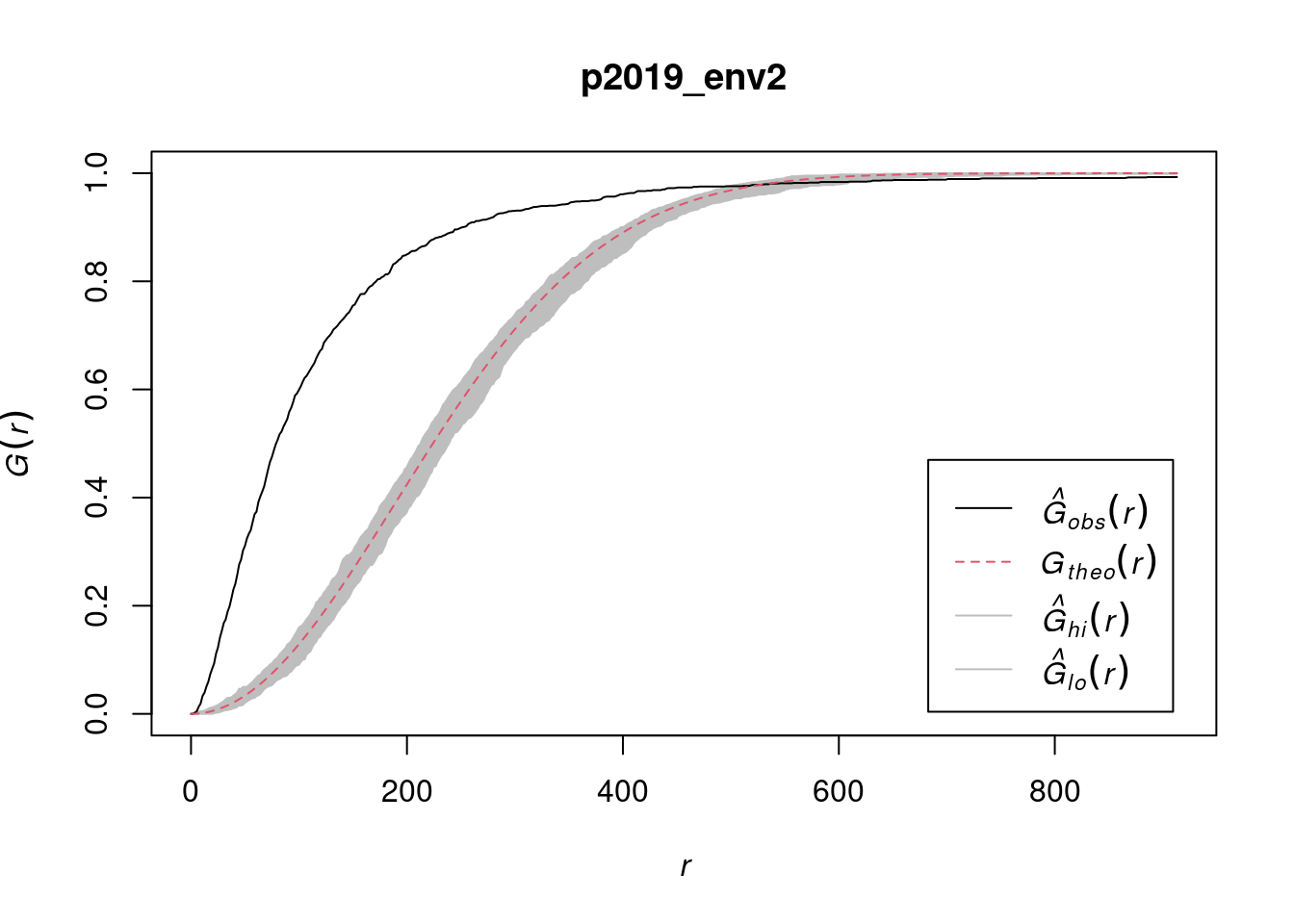

p2019_env1 = envelope(p2019_ppp, Kest, nsim = 99, 
                      funargs = list(correction = "none"))
plot(p2019_env1)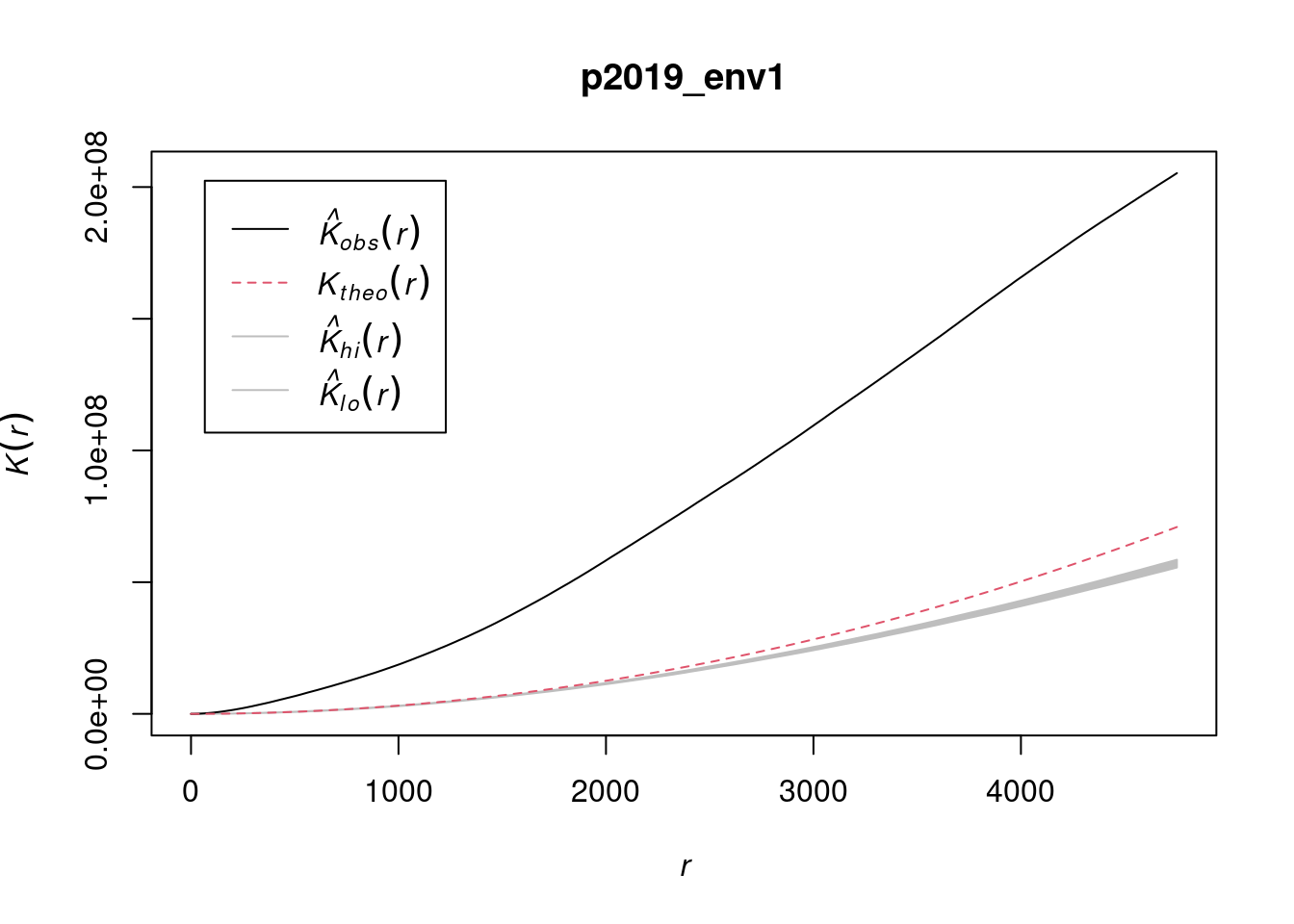

3.3 Wskaźnik Clarka-Evansa

Wskaźnik Clarka-Evansa (1954) określa stosunek między rzeczywistą średnią odległością od najbliższego sąsiada, a oczekiwaną dla rozkładu losowego.

Wartości niższe od 1 wskazują na występowanie skupień punktów
Wartość równa 1 wskazuje na losowy rozkład punktów
Wartości wyższe od 1 wskazują na bardziej regularny ich rozkład (np., dla regularnej siatki heksagonalnej wartość wskaźnika wynosi 2,15)

Wskaźnik Clarka-Evansa (1954) obliczany jest wykorzystując funkcję clarkevans() z pakietu spatstat().

clarkevans(p2019_ppp)[[1]]

[1] 0.5152518

Wartość wskaźnika wskazuje na występowanie skupień punktów.

4 Przykład 2: Rozkład przestrzenny szkół w Poznaniu

W poniższym przykładzie przeanalizowano przestrzenny rozkład szkół podstawowych w Poznaniu wykorzystując metody oparte na odległości:

statystyki najbliższego sąsiada
funkcje podsumowujące G, K Ripley’a
wskaźnik Clarka-Evansa

library(sf)
library(spatstat)
#wczytanie danych przestrzennych. Granica jest wykorzystywana wyłącznie do wizualizacji danych. 
szkoly = read_sf("data/out_poznan_szkoly.gpkg", layer = "szkoly")
granica = read_sf("data/out_poznan_szkoly.gpkg", layer = "granica")

#konwersja do obiektu klasy ppp 
szkoly_ppp = as.ppp(szkoly, w = granica_ppp)

4.1 Statystyki najbliższego sąsiada

Wykorzystując funkcję nndist tworzony jest wektor wartości zawierający odległość do najbliższego sąsiada. Wektor ten następnie podsumowywany jest za pomocą statystyk opisowych oraz wykresów (histogramu, dystrybuanty).

# obliczenie odległości do najbliższego sąsiada 
szkoly_nn = nndist(szkoly_ppp)
szkoly_nn_df = data.frame(shortest_distance = szkoly_nn)
summary(szkoly_nn)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  11.56   25.36   54.13  372.06  497.66 2902.80

library(ggplot2)
ggplot(szkoly_nn_df, aes(x = shortest_distance)) + 
  geom_histogram() + 
  labs(x = "Odległość do najbliższego sąsiada [km]") + 
  theme_bw()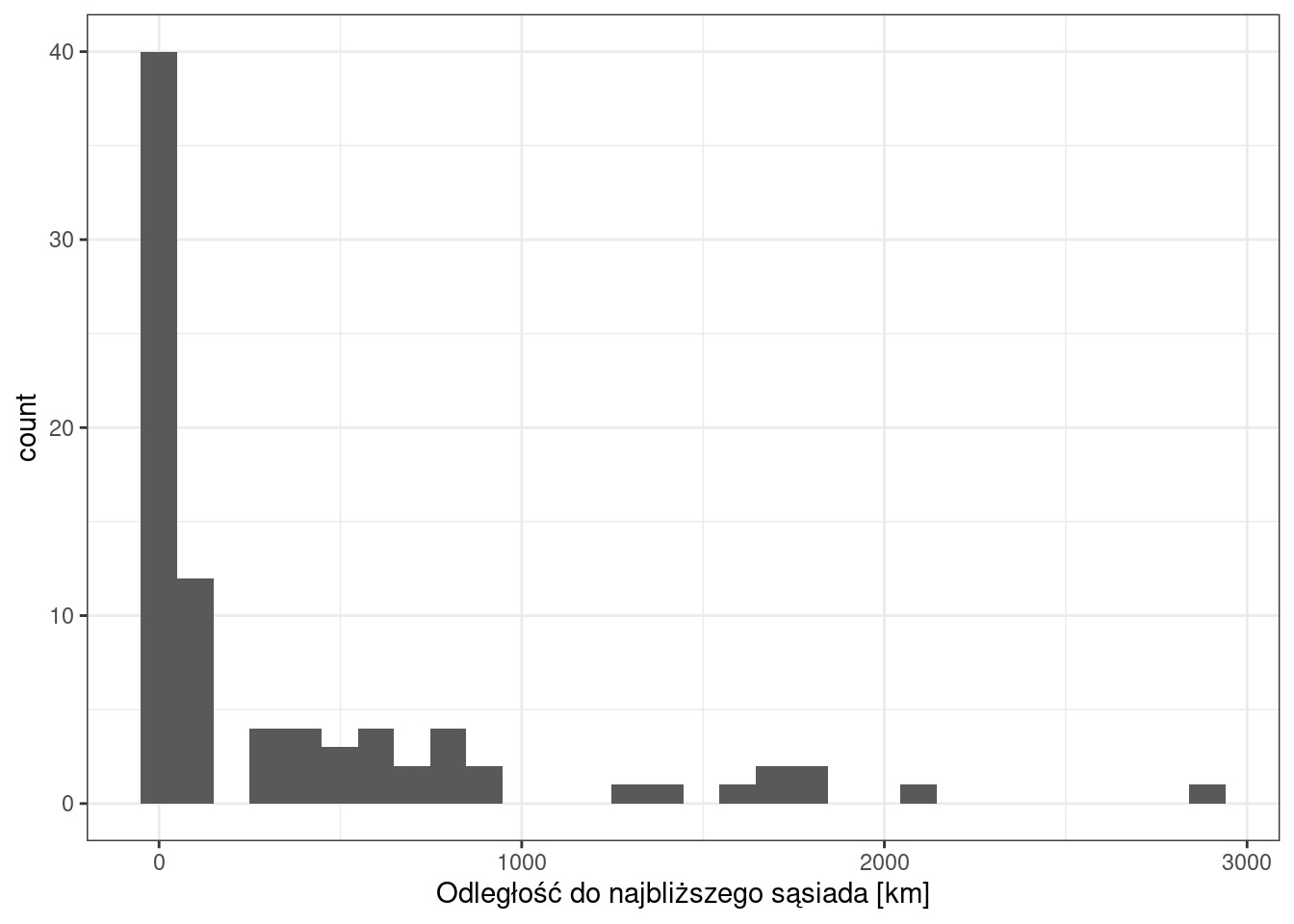

# cumulative distribution funcion 
## stat_ecdf - oblicza cdf (cumulative distribution funcion)
ggplot(szkoly_nn_df, aes(shortest_distance)) + 
  stat_ecdf(aes(ymin = 0, ymax = after_stat(y)), geom = "ribbon", fill = "grey95")+
  stat_ecdf() +
  labs(x = "Odległość do najbliższego sąsiada (km)",
       y = "Udział punktów w zbiorze danyh (%)") +
  scale_y_continuous(labels = scales::percent) + 
  theme_bw()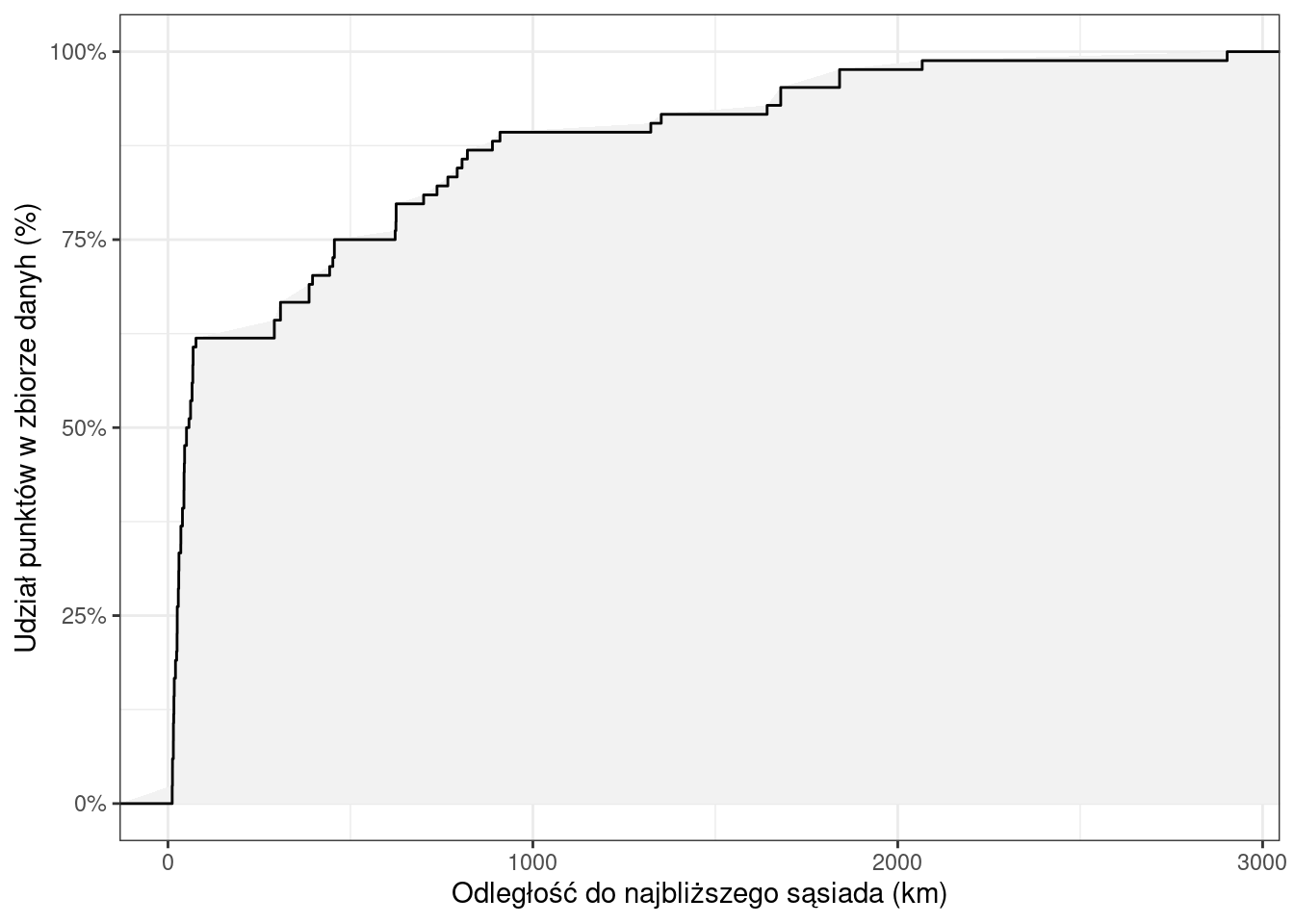

4.2 Funkcje podsumowujące G, K Ripley’a

Wykorzystując funkcje Gest(), Kest() oraz envelope() obliczane są funkcje podsumowujące G oraz K Ripley’a oraz testowana jest dla nich hipoteza dotycząca rozkładu przestrzennego punktów.

szkoly_env_g = envelope(szkoly_ppp, Gest, nsim = 99, 
                      funargs = list(correction = "none"))
plot(szkoly_env_g)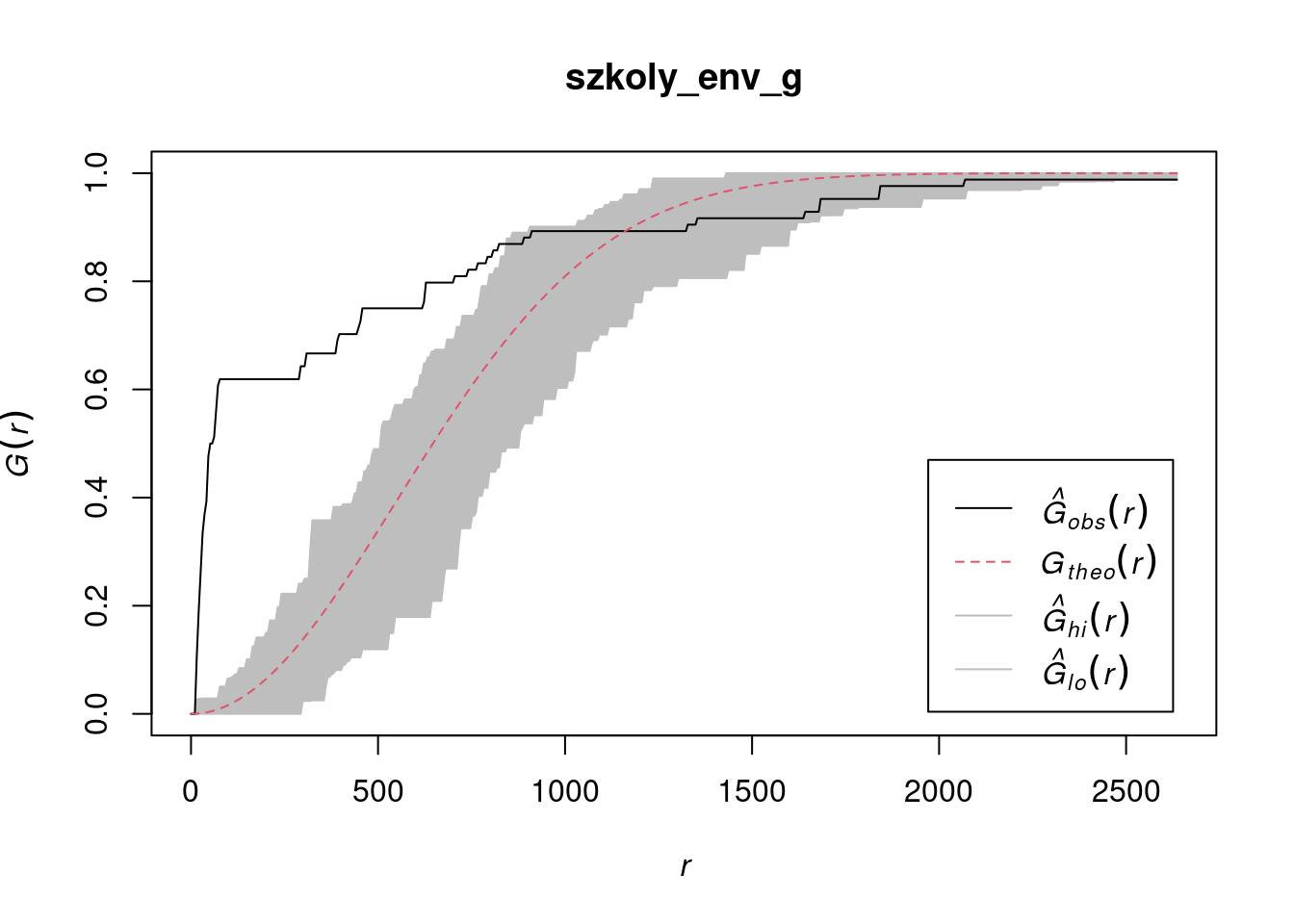

szkoly_env_k = envelope(szkoly_ppp, Kest, nsim = 99, 
                      funargs = list(correction = "none"))
plot(szkoly_env_k)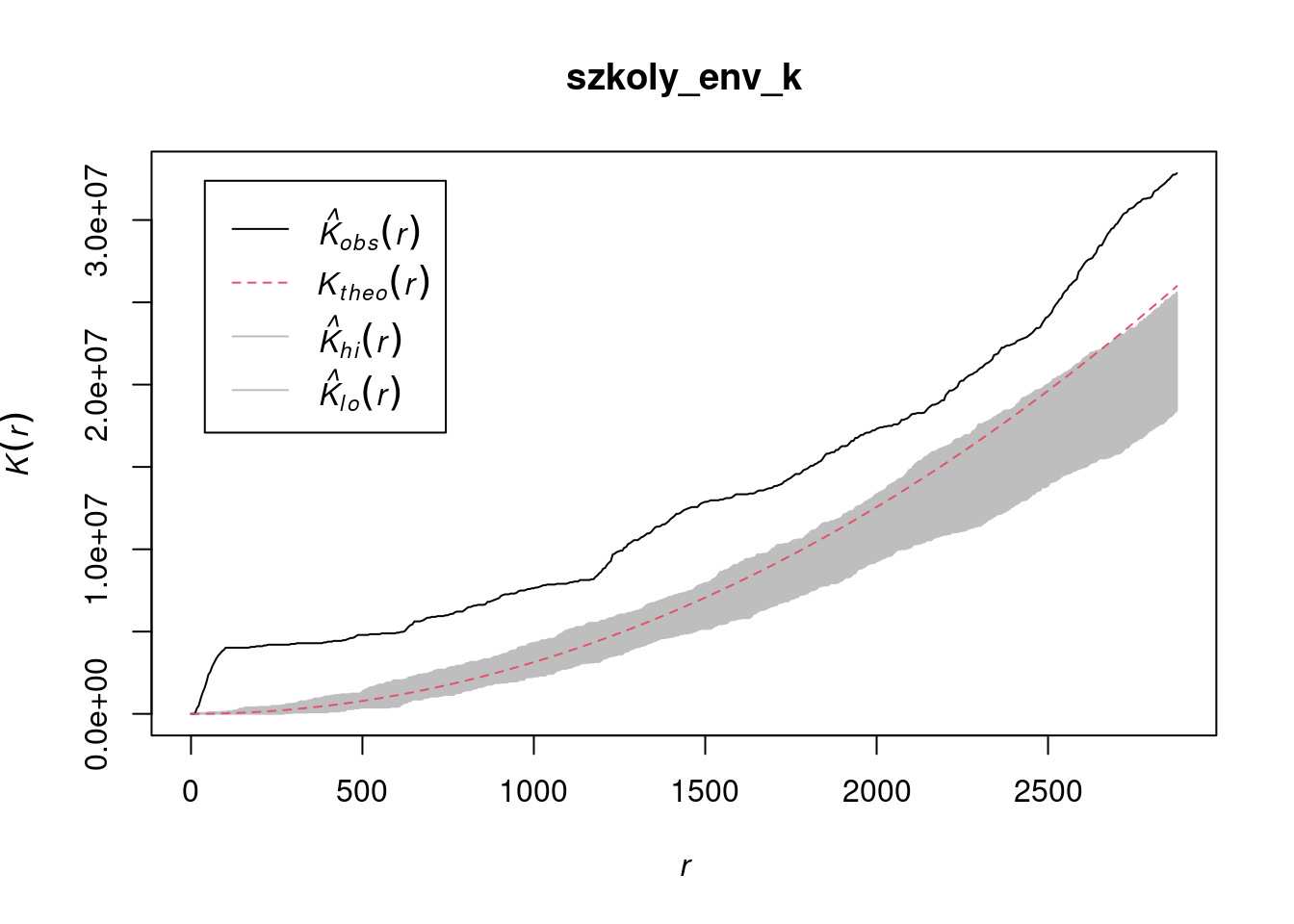

4.3 Wskaźnik Clarka-Evansa

clarkevans(szkoly_ppp)[[1]]

[1] 0.5404279

Jaki jest rozkład szkół w Poznaniu? Zintepretuj powyższe wyniki.