library(sf)Linking to GEOS 3.10.2, GDAL 3.4.1, PROJ 8.2.1; sf_use_s2() is TRUE# dane punktowe
p2019 = read_sf("data/przestepstwa_2019.gpkg")
#granica miasta Poznań
pzn = read_sf("data/pzn_borders.gpkg")Analiza rozkładu przestrzennego danych punktowych w R
1 Wprowadzenie
Analiza rozkładu przestrzennego danych punktowych ma na celu określenie w jaki sposób obiekty/zdarzenia są rozmieszczone w przestrzeni.
- Czy punkty są rozmieszczone losowo? (tzn. na ich rozmieszczenie nie działa żaden czynnik lub zależą od wielu czynników które się wzajemnie znoszą)
- Czy punkty są romieszczone regularnie? (tj. efekt świafomego działania, nie jest to proces naturalny)
- Czy występują skupiska (klastry) punktów? (tzn. na rozmieszczenie punktów wpływa jakiś czynnik)
1.1 Metody: Statystyki centrograficzne
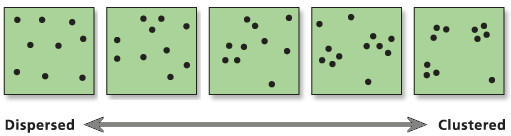
Statystyki centrograficzne stanowią przestrzenną modyfikację statystyk opisowych w klasycznej statystyce. Są podstawową formą opisu rozkładu przestrzennego danych punktowych. Do statystyk centrograficznych zalicza się:
- średnią centralną - punkt o współrzędnych stanowiących średnią arytmetyczną długości i szerokości geograficznej obiektów rozproszonych w przestrzeni
- odległość standardową - określa średnią odległość puntków od punktu centralnego (centroidu) i stanowi absolutną miarę roproszenia punktów w przestrzeni
- elipsę odchylenia standardowego - pozwala na określenia kierunków rozrzutu obiektów (obserwacji) w przestrzeni
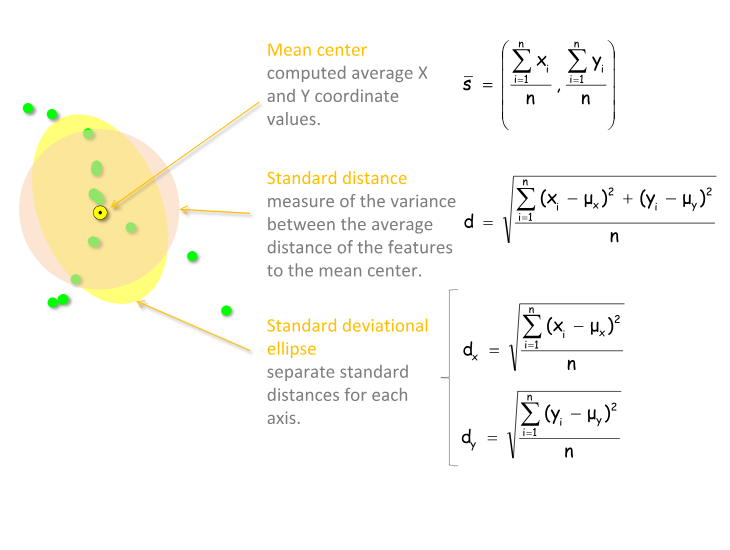
Żródło: https://mgimond.github.io/Spatial/chp11_0.html#centrography
1.2 Metody oparte na analizie intensywności
Metody oparte na analizie intensywności analizują rozkład przestrzenny punktów pod względem badanego obszaru.
intensywność zdarzenia (event) jest stała dla całego obszaru
- średnia intensywność (\(\lambda\)) obliczana jako liczba zdarzeń \(n\) na jednostkę powierzchni \(a\) (\(\lambda = \frac{n}{a}\))
intensywność zmienia się wraz z lokalizacją
- test zliczania w kwadratach (ang. quadrat count test)
- estymacja gęstości jądra (ang. kernel density estimation)
1.3 Metody oparte na odległości
Metody oparte na odległości wykorzystują informację o odległości między każdą lokalizacją pomiaru/obserwacji, a najbliższym innym pomiarem/obserwacją.
statystyki najbliższego sąsiada - wykorzystywane do określenia rozkładu odległości pomiędzy każdą lokalizacją pomiaru/obserwacji, a najbliższym innym pomiarem/obserwacją;
funkcja G - podsumowuje rozkład odległości do najbliższego sąsiada w postaci dystrybuanty, wykorzystywana do porównania odległości teoretycznych wynikających z losowego rozkładu punktów z odległościami empirycznymi obliczonymi na podstawie danych;
funkcja K Ripley’a - wykorzystywana do porównania odległości teoretycznych wynikających z losowego rozkładu punktów z odległościami empirycznymi obliczonymi na podstawie danych;
wskaźnik Clarka-Evansa (1954) - stosunek między rzeczywistą średnią odległością od najbliższego sąsiada, a oczekiwaną dla rozkładu losowego.
2 Analiza danych punktowych w R
2.1 Pakiet sfdep
Pakiet sfdep pozwala na obliczanie różnych statystyk centrograficznych w oparciu o dane punktowe wczytane za pomocą pakietu sf:
center_mean()- średnia centralnastd_distance()- odległość standardowastd_dev_ellipse()- elipsa odchylenia standardowego
2.2 Pakiet spatstat
Pakiet spatstat dostarcza szeregu funkcji do analizy rozkładu danych punktowych w R. Wzór punktowy w pakiecie spatstat jest obiektem klasy ppp (plannar point pattern). Wiele funkcji z pakietu wymaga zdefiniowania także obszaru analizy (tzw. okna, window).
Pakiet spatstat zawiera funkcje pozwalające na zastosowanie:
metod opartych na analizie intensywności:
as.ppp- konwertuje dane na obiekty klasy ppp. Wymaga podania obiektu oraz określenia obszaru analizy.as.owin- tworzy okno (window) na podstawie innego obiektu (np. granic miasta Poznania)
metod opartych na odległości
pairdist()- zwraca macierz z odległościami między wszystkimi parami punktów w zbiorze danychnndist()- zwraca wektor odległości od punktu do najbliżego sąsiada; odległości te są uzyskiwane przez sortowanie odległości między parami punktów i wybierana jest minimalna wartości dla każdego punktudistmap()- oblicza odległość od każdej komórki do najbliższego punktu i zwraca mapę rastrową.clarkevans()- obliczenie wskaźnika Clarka-EvansaGest()- obliczenie funkcji GKest()- obliczenie funkcji K Ripley’aenvelope()- estowania hipotezy zerowej dla funkcji G, K Ripley’aquadratcount()- test zliczania w kwadratach
3 Przykład 1: Przestępczość w Poznaniu
3.1 Dane
W przykładzie 1 wykorzystano dane dotyczące przestępczości w Poznaniu (plik przestepstwa_2019.gpkg) wraz z granicą miasta Poznania (plik pzn_borders.gpkg). Do podsumowania rozkładu przestępczości wykorzystano statystyki centrograficzne. Plik przestepstwa_2019.gpkg zawiera tylko kolumnę geom bez dodatkowych atrybutów.
head(p2019)Simple feature collection with 6 features and 0 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 353099.3 ymin: 503305.9 xmax: 361715.2 ymax: 510415
Projected CRS: ETRF2000-PL / CS92
# A tibble: 6 × 1
geom
<POINT [m]>
1 (361379.5 503546.3)
2 (361691.3 503694.6)
3 (360347.3 506216)
4 (353099.3 504204.1)
5 (361715.2 503305.9)
6 (360260.9 510415)library(tmap)
tm_shape(pzn) +
tm_borders() +
tm_shape(p2019) +
tm_dots()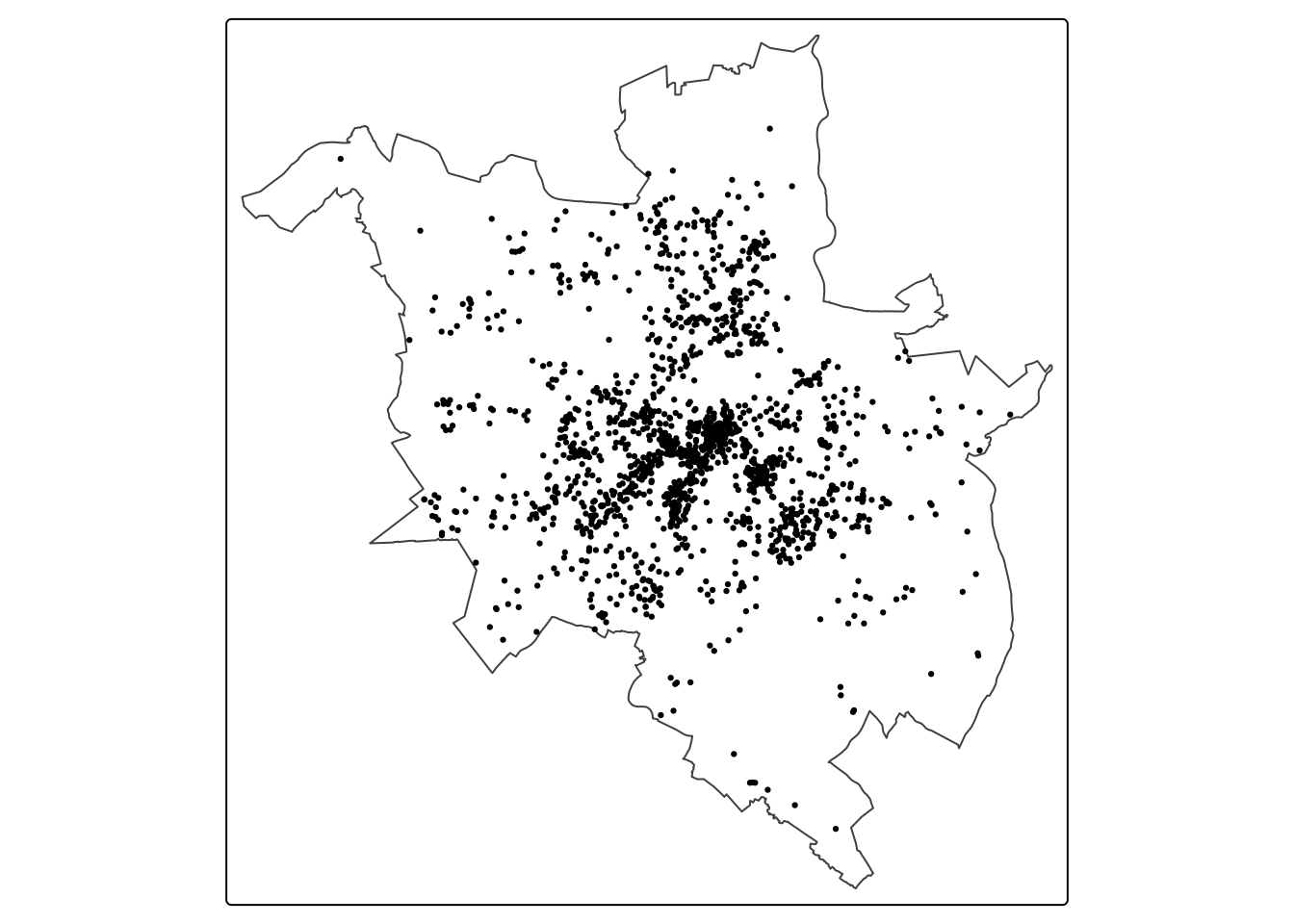
3.2 Obliczanie statystyk centrograficznych
Statystyki centrograficzne (średnia centralna, odległość standardowa) mogą być obliczone na podstawie ramki danych zawierającej współrzędne x oraz y.
Funkcja st_coordinates() z pakietu sf pozwala na wydobycie współrzędnych z obiektu punktowego klasy sf oraz stworzenie ramki danych zawierającej dwie kolumny: x oraz y.
library(sf)
p2019_coords = st_coordinates(p2019)
head(p2019_coords) X Y
[1,] 361379.5 503546.3
[2,] 361691.3 503694.6
[3,] 360347.3 506216.0
[4,] 353099.3 504204.1
[5,] 361715.2 503305.9
[6,] 360260.9 510415.03.2.1 Średnia centralna
Średnia centralna wyznaczona jest przez punkt o współrzędnych \(\overline{x_c}\), \(\overline{y_c}\). Średnia centralna obliczana jest jako średnia arytmetyczna współrzędnych x oraz y.
\[\overline{x_c} = \frac{\sum_{i=1}^{n} x_i}{n}\]
\[\overline{y_c} = \frac{\sum_{i=1}^{n} y_i}{n}\]
Średnią centralną obliczamy poprzez wyliczenie średniej wartości dla kolumny X oraz Y.
# mean center
mc = apply(p2019_coords, 2, mean)
mc X Y
358716.4 506363.5 3.2.2 Odległość standardowa
Odległość standardowa określa średnią odległość puntków (\(x_{i}\), \(y_{i}\)) od punktu centralnego (centroidu, (\(\overline{x_c}\), \(\overline{y_c}\))) i obliczana jest wg wzoru:
\[d = \sqrt{\frac{\sum_{i=1}^{n} d_{ic}^2}{n}}\]
\[d_{ic}^2 = (x_i - \overline{x_c})^2 + (y_i - \overline{y_c})^2 \]
W powyższym wzorze
- \(x_{i}\) oznacza współrzędną x dla każdego punktu (p2019_coords[,1] ),
- \(y_{i}\) oznacza współrzędną y dla każdego punktu (p2019_coords[,2]),
- \(\overline{x_c}\) to współrzędna x dla średniej centralnej (mc[1]),
- \(\overline{y_c}\) to współrzędna y dla średniej centralnej (mc[2]).
# standard distance
sd = sqrt(sum((p2019_coords[,1] - mc[1])^2 + (p2019_coords[,2] - mc[2])^2) / nrow(p2019_coords))
sd[1] 3886.9353.3 Wizualizacja średniej centralnej i odległości standardowej
Wizualizacja średniej centralnej wymaga utworzenia obiektu przestrzennego w oparciu o współrzędne punktu. W tym celu wykorzystanie zostanie funkcja st_point() oraz st_sfc() z pakietu sf.
#Przekształcenie obiektu mc na obiekt przestrzenny klasy sfc_POINT
mc_point = st_sfc(st_point(mc), crs = st_crs(p2019))plot(mc_point)Odległość standardowa graficznie przedstawiana jest jako koło o środku w punkcie wyznaczonym przez średnią centralną oraz promieniu równym odległości standardowej. Do stworzenia obiektu przestrzennego przedstawiającego zasięg odległości standardowej wykorzystana zostanie funkcja st_buffer() z pakietu sf.
#wyznaczenie strefy buforowej wokół średniej centralnej o promieniu równym odległości standardowej
sd_buffer = st_buffer(mc_point, sd)tm_shape(pzn) +
tm_borders() +
tm_shape(p2019) +
tm_dots() +
tm_shape(mc_point) +
tm_symbols(fill = "red") +
tm_shape(sd_buffer) +
tm_borders(col = "red", lwd = 2)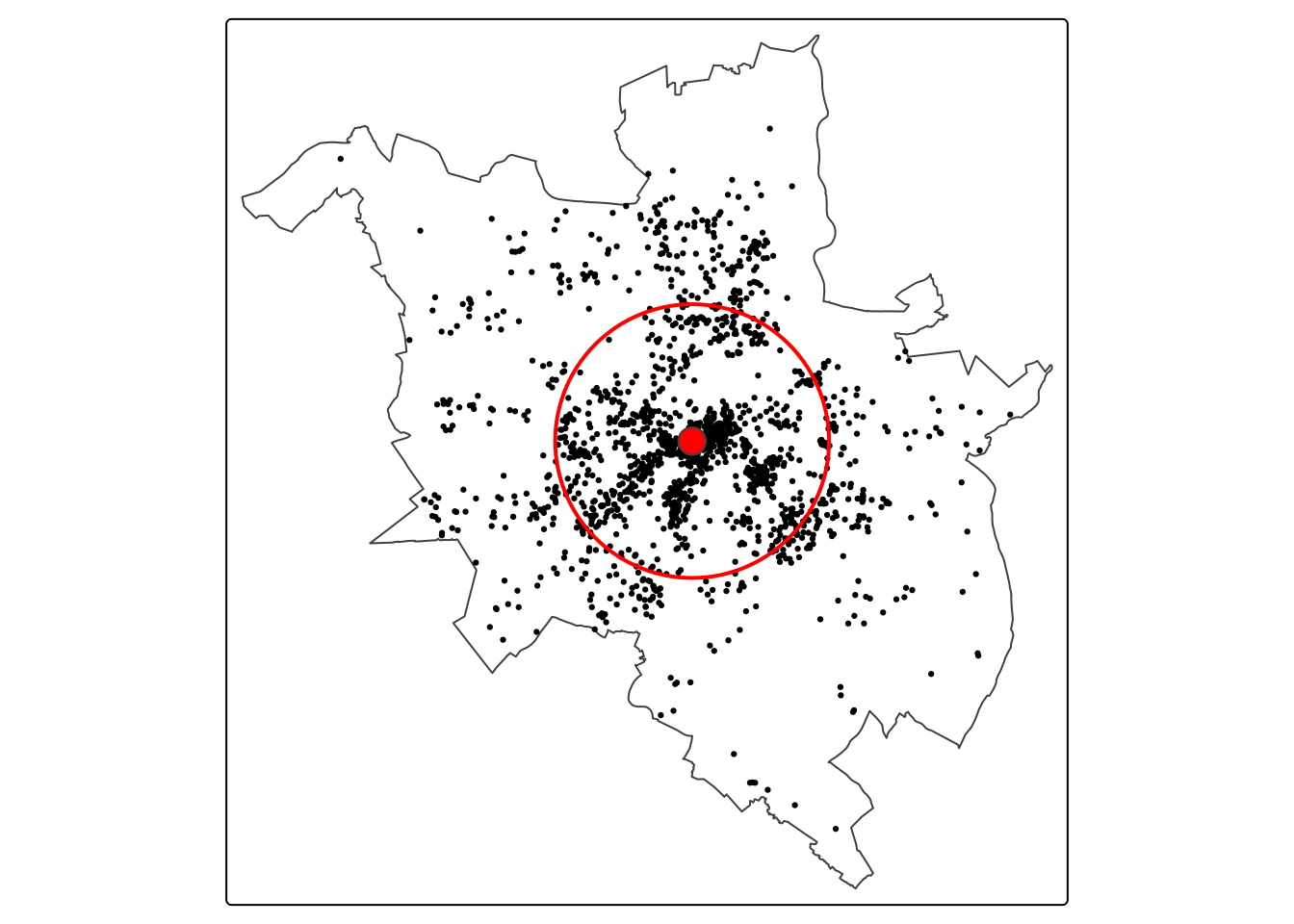
Obliczanie statystyk centrograficznych - pakiet sfdep
Statystyki centrograficzne w R można wyznaczyć używając funkcji z pakietu sfdep:
center_mean()- średnia centralna
library(pracma)
library(sfdep)
#srednia centralna
mc_point2 = center_mean(p2019)std_distance()- odległość standardowa
library(pracma)
library(sfdep)
# odległość standardowa
sd2 = std_distance(p2019) #zwraca wartość z odległością
sd2_buffer = st_buffer(mc_point2, sd2) #zwraca obiekt przestrzennystd_dev_ellipse()- elipsa odchylenia standardowego
library(pracma)
library(sfdep)
# funkcja std_dev_ellipse zwraca parametry elipsy, st_ellipse tworzy na ich podstawie obiekt liniowy
p2019_e = std_dev_ellipse(p2019)
p2019_e = st_ellipse(p2019_e, sx = p2019_e$sx, sy = p2019_e$sy)3.4 Wizualizacja statystyk centrograficznych
tm_shape(pzn) +
tm_borders() +
tm_shape(p2019) +
tm_dots() +
tm_shape(mc_point) +
tm_dots(fill = "red", size = 2) +
tm_shape(sd2_buffer) +
tm_borders(col = "red", lwd = 3) +
tm_shape(p2019_e) +
tm_lines(col = "darkgreen", lwd = 3)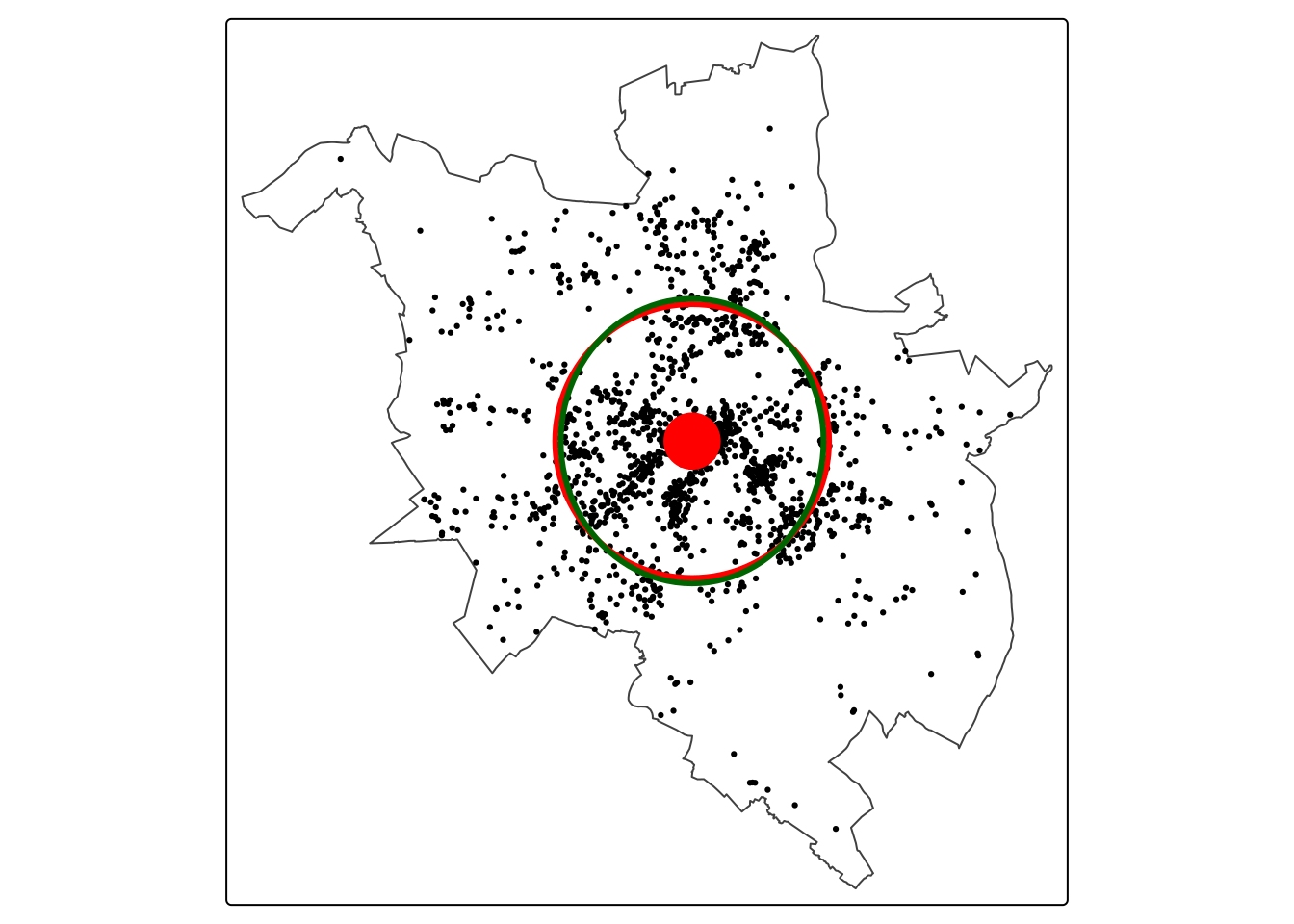
4 Przykład 2: Rozkład przestrzenny szkół w Poznaniu
4.1 Dane
W drugim przykładzie wykorzystano dane pozyskane z BDOT10k z warstwy przedstawiającej budynki (OT_BUBD_A) oraz granice administracyjne (OT_ADJA_A) do przeanalizowania rozkładu przestrzennego szkół podstawowych w Poznaniu.
Granica miasta Pozania została pozyskana z warstwy OT_ADJA_A.
granica = read_sf("data/bdot10k/PL.PZGiK.308.BDOT10k.3064__OT_ADJA_A.gpkg")
granica = granica[granica$RODZAJ == "powiat", "geometria"]Warstwa OT_BUBD_A jest warstwą poligonową zawierającą różne typy budynków.
budynki <- read_sf("data/bdot10k/PL.PZGiK.308.BDOT10k.3064__OT_BUBD_A.gpkg")head(budynki)Simple feature collection with 6 features and 19 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 359155.6 ymin: 500467.5 xmax: 362596.6 ymax: 502295.9
Projected CRS: ETRF2000-PL / CS92
# A tibble: 6 × 20
TERYT LOKALNYID PRZESTRZENNAZW WERSJA POCZATEKWERSJIOBIEKTU
<chr> <chr> <chr> <dttm> <dttm>
1 3064 3c25a636-5303-… PL.PZGiK.308.… 2023-12-31 12:00:00 2023-12-31 12:00:00
2 3064 12e66037-0d58-… PL.PZGiK.308.… 2023-12-31 12:00:00 2023-12-31 12:00:00
3 3064 021dfd88-65df-… PL.PZGiK.308.… 2023-12-31 12:00:00 2023-12-31 12:00:00
4 3064 5b5acb18-3c3a-… PL.PZGiK.308.… 2023-12-31 12:00:00 2023-12-31 12:00:00
5 3064 a4b459f2-551c-… PL.PZGiK.308.… 2023-12-31 12:00:00 2023-12-31 12:00:00
6 3064 3fddfa4f-6f68-… PL.PZGiK.308.… 2023-12-31 12:00:00 2023-12-31 12:00:00
# ℹ 15 more variables: OZNACZENIEZMIANY <chr>,
# ZRODLODANYCHGEOMETRYCZNYCH <chr>, KATEGORIAISTNIENIA <chr>, UWAGI <chr>,
# INFORMACJADODATKOWA <chr>, KODKARTO10K <chr>, SKROTKARTOGRAFICZNY <chr>,
# KODKST <chr>, FUNKCJAOGOLNABUDYNKU <chr>, PRZEWAZAJACAFUNKCJABUDYNKU <chr>,
# LICZBAKONDYGNACJI <dbl>, NAZWA <chr>, FSBUD <chr>, IDEGIB <chr>,
# geometria <POLYGON [m]>Informacje o typach budynków zapisane są w dwóch kolumnach: FUNKCJAOGOLNABUDYNKU oraz PRZEWAZAJACAFUNKCJABUDYNKU.
unique(budynki$FUNKCJAOGOLNABUDYNKU) [1] "budynki szpitali i inne budynki opieki zdrowotnej"
[2] "budynki transportu i łączności"
[3] "budynki mieszkalne"
[4] "budynki produkcyjne, usługowe i gospodarcze dla rolnictwa"
[5] "zbiorniki, silosy i budynki magazynowe"
[6] "budynki przemysłowe"
[7] "budynki oświaty, nauki i kultury oraz budynki sportowe"
[8] "budynki handlowo-usługowe"
[9] "pozostałe budynki niemieszkalne"
[10] "budynki biurowe" funcja_szczegolowa_budynku = unique(budynki$PRZEWAZAJACAFUNKCJABUDYNKU)4.1.1 Przygotowanie danych do analizy
Selekcja budynków w kategorii szkoła podstawowa
Szkoły podstawowe to kategoria określona jako przeważająca funkcja budynku (kolumna PRZEWAZAJACAFUNKCJABUDYNKU).
szkoly_podstawowe = budynki[budynki$PRZEWAZAJACAFUNKCJABUDYNKU%in%c("szkoła podstawowa"),]Konwersja warstwy poligonowej na punktową
Warstwa BUBD_A jest warstwą poligonową. Aby zamienić budynki (poligony) na punkty należy użyć funkcji st_centroid() z pakietu sf.
szkoly_pkt = st_centroid(szkoly_podstawowe[, "geometria"])Zapisanie warstw
st_write(szkoly_pkt, dsn = "data/out_poznan_szkoly.gpkg", layer = "szkoly", delete_dsn = TRUE)Deleting source `data/out_poznan_szkoly.gpkg' using driver `GPKG'
Writing layer `szkoly' to data source
`data/out_poznan_szkoly.gpkg' using driver `GPKG'
Writing 84 features with 0 fields and geometry type Point.st_write(granica, dsn = "data/out_poznan_szkoly.gpkg", layer = "granica")Writing layer `granica' to data source
`data/out_poznan_szkoly.gpkg' using driver `GPKG'
Writing 1 features with 0 fields and geometry type Polygon.4.1.2 Lokalizacja szkół podstawowych w mieście Poznań.
Do wizualizacji lokalizacji szkół podstawowych w mieście Poznań wykorzystano pakiet tmap().
library(tmap)
tm_shape(granica) +
tm_borders(col = "black") +
tm_shape(szkoly_pkt) +
tm_dots(col = "black", size = 0.7)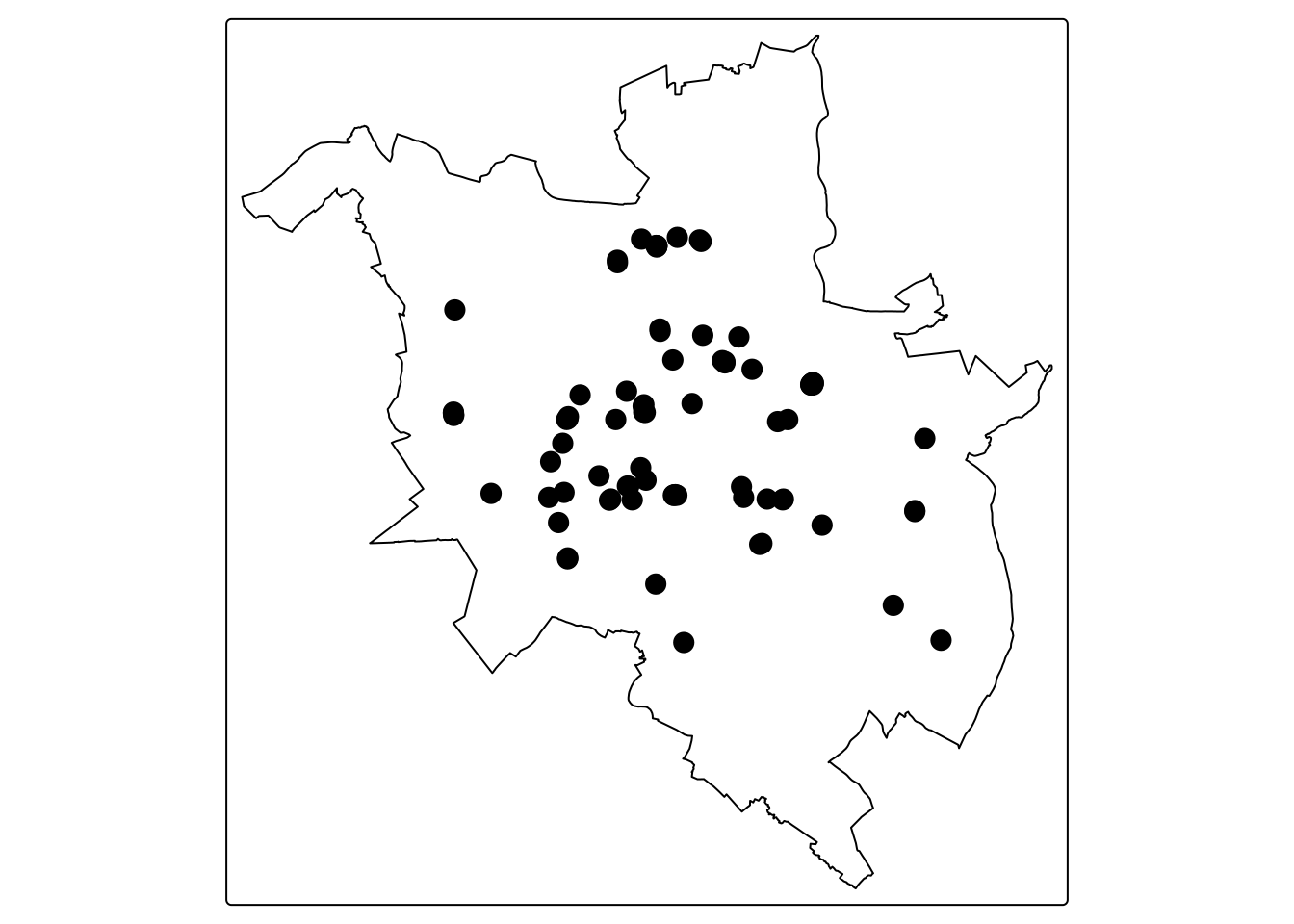
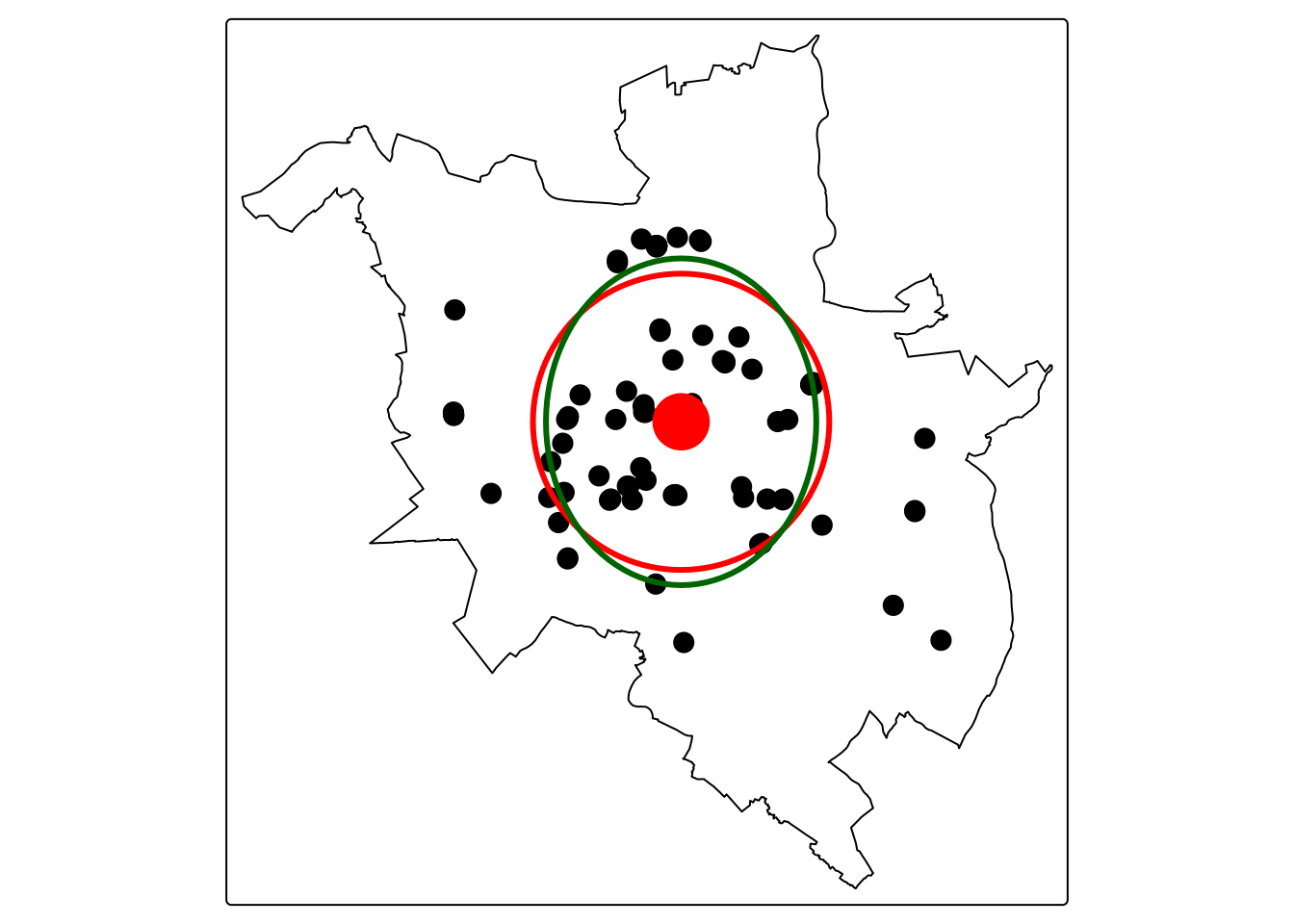
4.2 Statystyki centrograficzne
Wykorzystując funkcje z pakietu sfdep zostały obliczone statystyki centrograficzne: średnia centralna (funkcja center_mean()), odległość standardowa (funkcja std_distance()), elipsa odchylenia standardowego (std_dev_ellipse()).
library(pracma)
library(sfdep)
#srednia centralna
mc_point2 = center_mean(szkoly_pkt)
# odległość standardowa
sd2 = std_distance(szkoly_pkt) #zwraca wartość z odległością
sd2_buffer = st_buffer(mc_point2, sd2) #zwraca obiekt przestrzenny
# funkcja std_dev_ellipse zwraca parametry elipsy, st_ellipse tworzy na ich podstawie obiekt liniowy
szkoly_pkt_e = std_dev_ellipse(szkoly_pkt)
szkoly_pkt_e = st_ellipse(szkoly_pkt_e, sx = szkoly_pkt_e$sx, sy = szkoly_pkt_e$sy)4.3 Wizualizacja statystyk centrograficznych
tm_shape(granica) +
tm_borders(col = "black") +
tm_shape(szkoly_pkt) +
tm_dots(fill = "black", size = 0.7) +
tm_shape(mc_point2) +
tm_dots(fill = "red", size = 2) +
tm_shape(sd2_buffer) +
tm_borders(col = "red", lwd = 3) +
tm_shape(szkoly_pkt_e) +
tm_lines(col = "darkgreen", lwd = 3)