Eksploracyjna analiza danych przestrzennych

Author

Anna Dmowska, Jakub Nowosad

library(tmap)
library(sf)
library(ggplot2)
library(dplyr)

1 Eksploracyjna analiza danych

Każda analiza danych przestrzennych powinna być poprzedzona eksploracyjną analizą danych. Celem eksploracyjnej analizy danych jest uzyskanie podstawowych informacji o analizowanych danych.
Sposób wykonania eksploracyjnej analizy danych (np. dobór wykorzystywanych metod) różni się w zależności od posiadanego zbioru danych, jak i od postawionego pytania.

1.1 Cele eksploracyjnej analizy danych

Ogólne cele eksploracyjnej analizy danych obejmują:

Przygotowanie ogólnej charakterystyki danych oraz badanego zjawiska.
Identyfikacja przestrzennego/czasowego typu próbkowania.
Ocena relacji zachodzących pomiędzy lokalizacją pomiaru/obserwacji, a czynnikami wpływającymi na zmienność przestrzenną badanych cech.

1.2 Eksploracyjna analiza nieprzestrzenna i przestrzenna

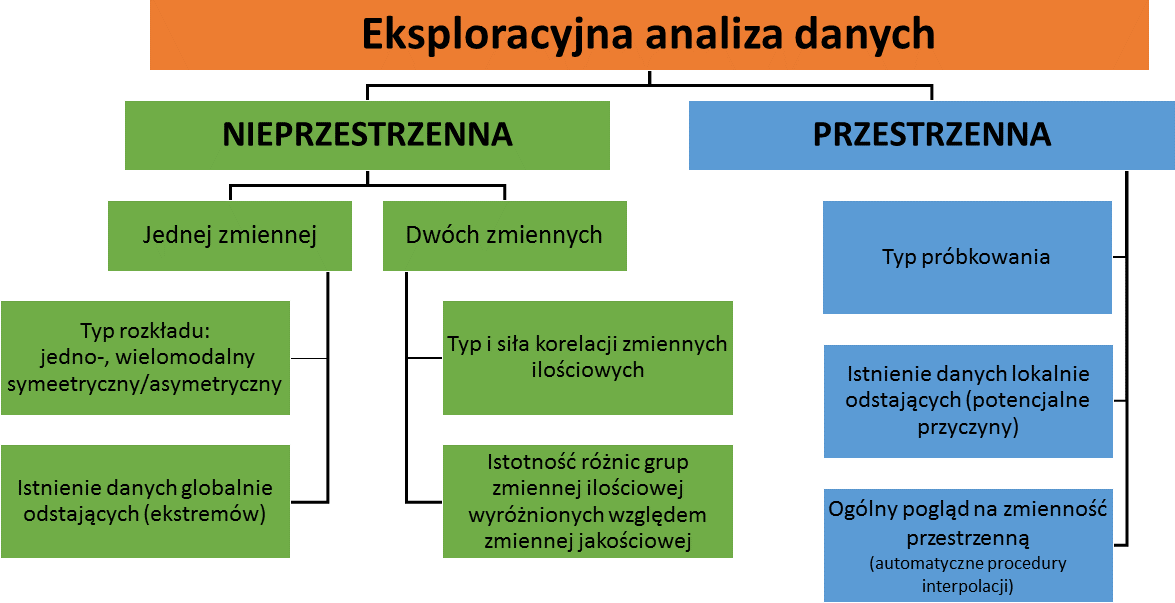
Eksploracyjna analiza danych dzieli się na analizę nieprzestrzenną i przestrzenną.

Nieprzestrzenna	Przestrzenna
w analizie uwzględniane są wartości atrybutów, a nie ich lokalizacja	podstawą analizy danych jest lokalizacja obserwacji
analiza statystyczna danych wykonywana w oparciu o tabelę atrybutów dołączoną do danych geoprzestrzennych
podstawowe statystyki opisowe, typ rozkładu danych, analiza korelacji, zmienność cechy w grupach	typ próbkowania, ogólny pogląd na zmienność przestrzenną zjawiska

2 Eksploracyjna analiza dla różnych typów danych

2.1 Statystyka punktów

Cel:

określenie w jaki sposób obiekty/zdarzenia są rozmieszczone w przestrzeni

Eksploracyjna analiza danych:

Sprawdzenie poprawności współrzędnych
Wgląd w typ próbkowania
Określenie zależności między lokalizacją, a innymi czynnikami (np. więcej włamań notuje się w obszarach z wysokimi cenami nieruchomości)

2.2 Statystyka powierzchni (dane poligonowe)

Cel:

analiza podobieństwa i różnic między obszarami/regionami
wyszukanie obszarów podobnych do siebie
znalezienie obszarów znacząco różnych od sąsiednich

Eksploracyjna analiza danych:

Charakterystyka statystyczna danych (statystyki podstawowe, wartości odstające globalnie, rozkład danych)
Sprawdzenie poprawności danych, w tym między innymi identyfikacja danych odstających lokalnie

2.3 Geostatystyka

Cel:

zrozumienie zmienności przestrzennej lub czasowej zjawiska
szacowanie wartości dla całego obszaru (dane ciągłe) na podstawie danych punktowych (estymacja)

Eksploracyjna analiza danych:

Charakterystyka statystyczna danych (statystyki podstawowe, wartości odstające globalnie, rozkład danych)
Sprawdzenie poprawności współrzędnych
Sprawdzenie poprawności danych, w tym między innymi identyfikacja danych odstających lokalnie
Wgląd w tym próbkowania
Ogólny pogląd na zmienność przestrzenną, wykorzystanie prostej automatycznej procedury interpolacji

3 Przykład 1. Analiza rozkładu temperatury powietrza

3.1 Dane i cel analizy

3.1.1 Cel

Celem analizy jest uzyskanie informacji o przestrzennym rozkładzie wartości temperatury w analizowanym obszarze. Dane punktowe przedstawiające lokalizacje pomiaru temperatury powietrza zostaną wykorzystane następnie w analizie geostatystycznej mającej w celu oszacowania wartości dla całego obszaru z wykorzystaniem jednej z geostatystycznych metod estymacji.

3.1.2 Dane

Dla analizowanego obszaru dysponujemy:

danymi punktowymi (punkty.csv) zapisanymi w pliku tekstowym zawierającymi lokalizacje, w których wykonano pomiary temperatury powietrza. Dla każdej lokalizacji dysponujemy także zestawem zmiennych dodatkowych (ndvi, wysokość n.p.m (srtm), klasa pokrycia terenu (clc)).
plikiem wektorowym w formacie .gpkg (granica.gpkg) zawierającym granicę obszaru analizy.

granica = read_sf("data/granica.gpkg")
#wczytanie danych oraz konwersja do klasy sf
pkt = read.csv("data/punkty.csv")
pkt = pkt[!is.na(pkt$temp), ]
punkty = st_as_sf(pkt, coords = c("x", "y"), crs = "EPSG:2180")

str(punkty)

Classes 'sf' and 'data.frame':  247 obs. of  6 variables:
 $ srtm    : num  176 150 273 187 260 ...
 $ clc     : int  1 1 NA 1 1 2 2 1 1 2 ...
 $ temp    : num  13.9 15.5 12.8 14.3 15.9 ...
 $ ndvi    : num  0.616 0.556 0.607 0.376 0.46 ...
 $ savi    : num  0.419 0.379 0.375 0.239 0.309 ...
 $ geometry:sfc_POINT of length 247; first list element:  'XY' num  750298 716732
 - attr(*, "sf_column")= chr "geometry"
 - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA NA
  ..- attr(*, "names")= chr [1:5] "srtm" "clc" "temp" "ndvi" ...

3.2 Eksploracyjna nieprzestrzenna analiza danych

3.2.1 Podsumowanie numeryczne

Podstawowe informacje o analizowanej zmiennej (w tym przykładzie temperatura powietrza temp) można uzyskać za pomocą funkcji summary(). Dodatkowo można obliczyć inne statystyki opisowe, np. odchylenie standardowe (funkcja sd).

summary(punkty$temp)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  7.883  12.003  14.941  15.273  17.630  24.945

sd(punkty$temp)

[1] 3.973076

3.2.2 Rozkład danych

Rozkład danych można przedstawić graficznie wykorzystując histogram (geom_histogram) lub estymator jądrowy gęstości (geom_density).

library(ggplot2)

ggplot(punkty, aes(temp)) + 
  geom_histogram() + 
  labs(x = "Zmienna temp", y = "Liczba obserwacji") + 
  theme_bw()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.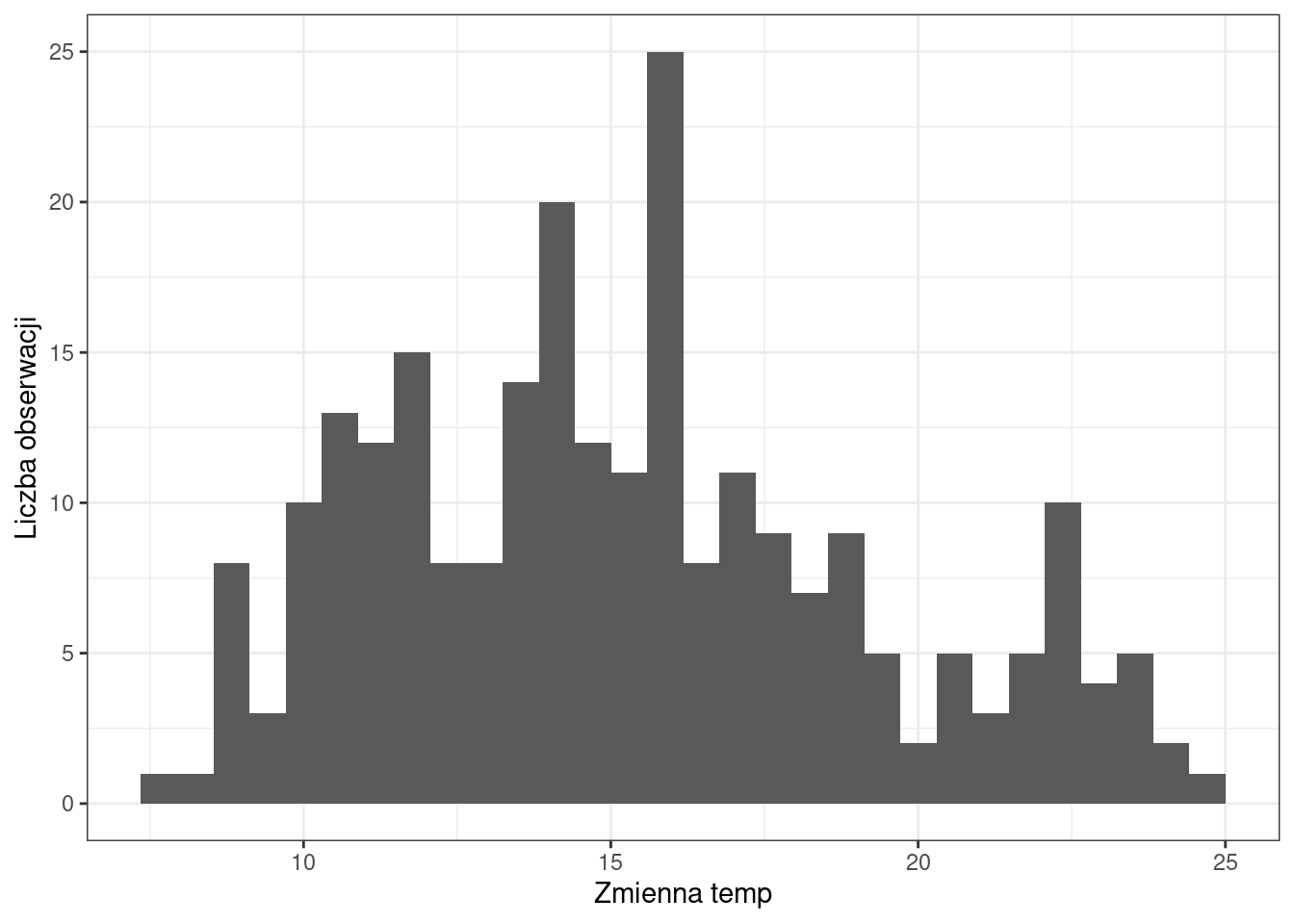

ggplot(punkty, aes(temp)) + geom_density() + theme_bw()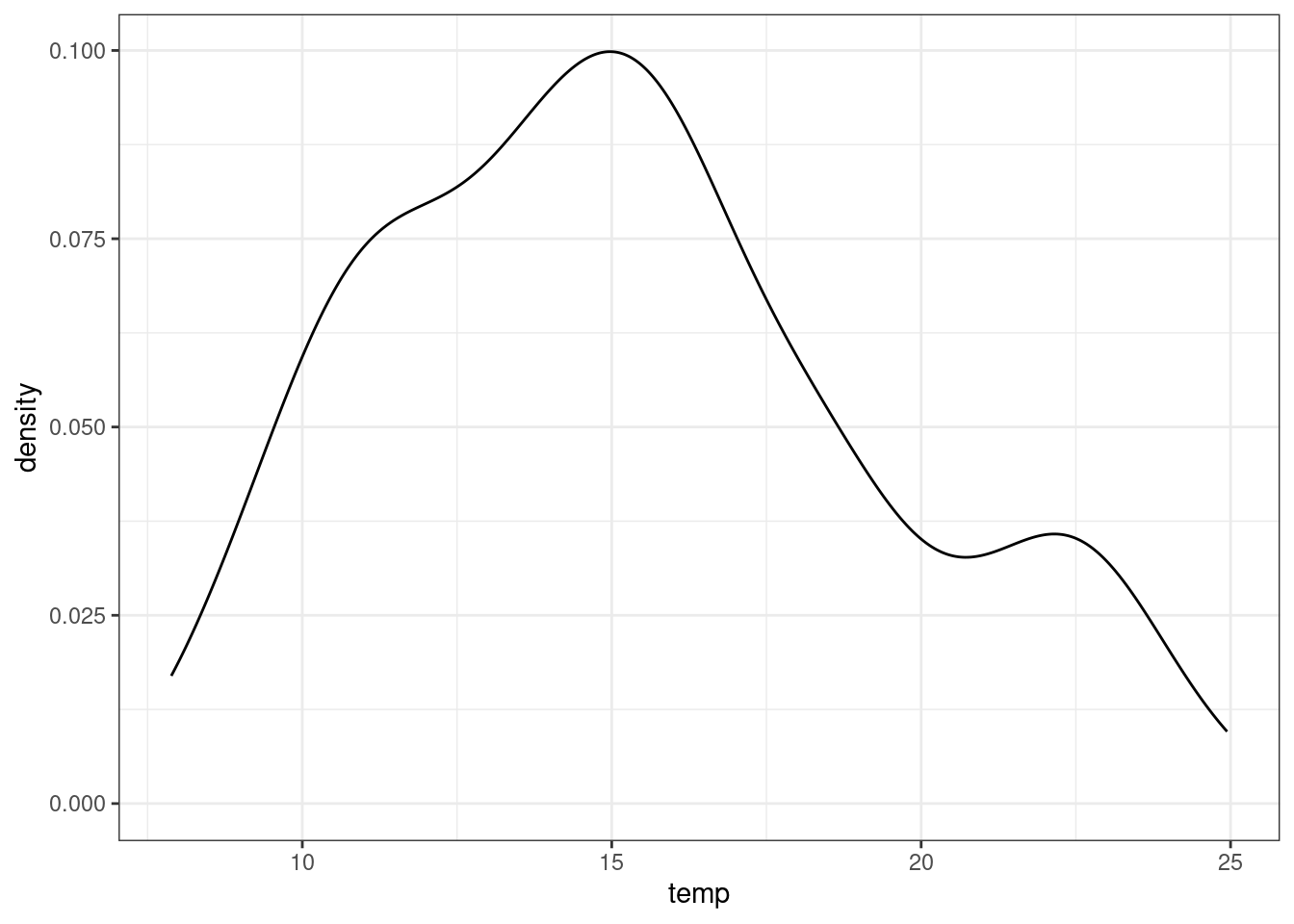

Dodatkowo rozkład danych można opisać za pomocą dwóch statystyk opisowych: skośności oraz kurtozy.

library(e1071)
skewness(punkty$temp)
kurtosis(punkty$temp)

3.2.3 Dane globalnie odstające

Dane globalnie odstające to bardzo niskie lub bardzo wysokie wartości względem pozostałych w zbiorze danych. Można je zidentyfikować poprzez wykonanie histogramu oraz obejrzenie rozkładu danych.

3.2.4 Zależność między temperaturą, a zmiennymi ndvi i srtm

Do określenia związku między zmiennymi ilościowymi (np. temperaturą a wartościami zmiennych srtm oraz ndvi) można wykorzystać wykres rozrzutu oraz miary korelacji (współczynnik korelacji liniowej lub współczynnik korelacji rang Spearmana). Poniżej wykonano wykresy rozrzutu pokazujące zależnośc między zmienną temp, a ndvi oraz zmienną temp, a srtm.

ggplot(punkty, aes(temp, ndvi)) +
  geom_point() +
  labs(x = "Zmienna temp", y = "Zmienna ndvi") + 
  theme_bw()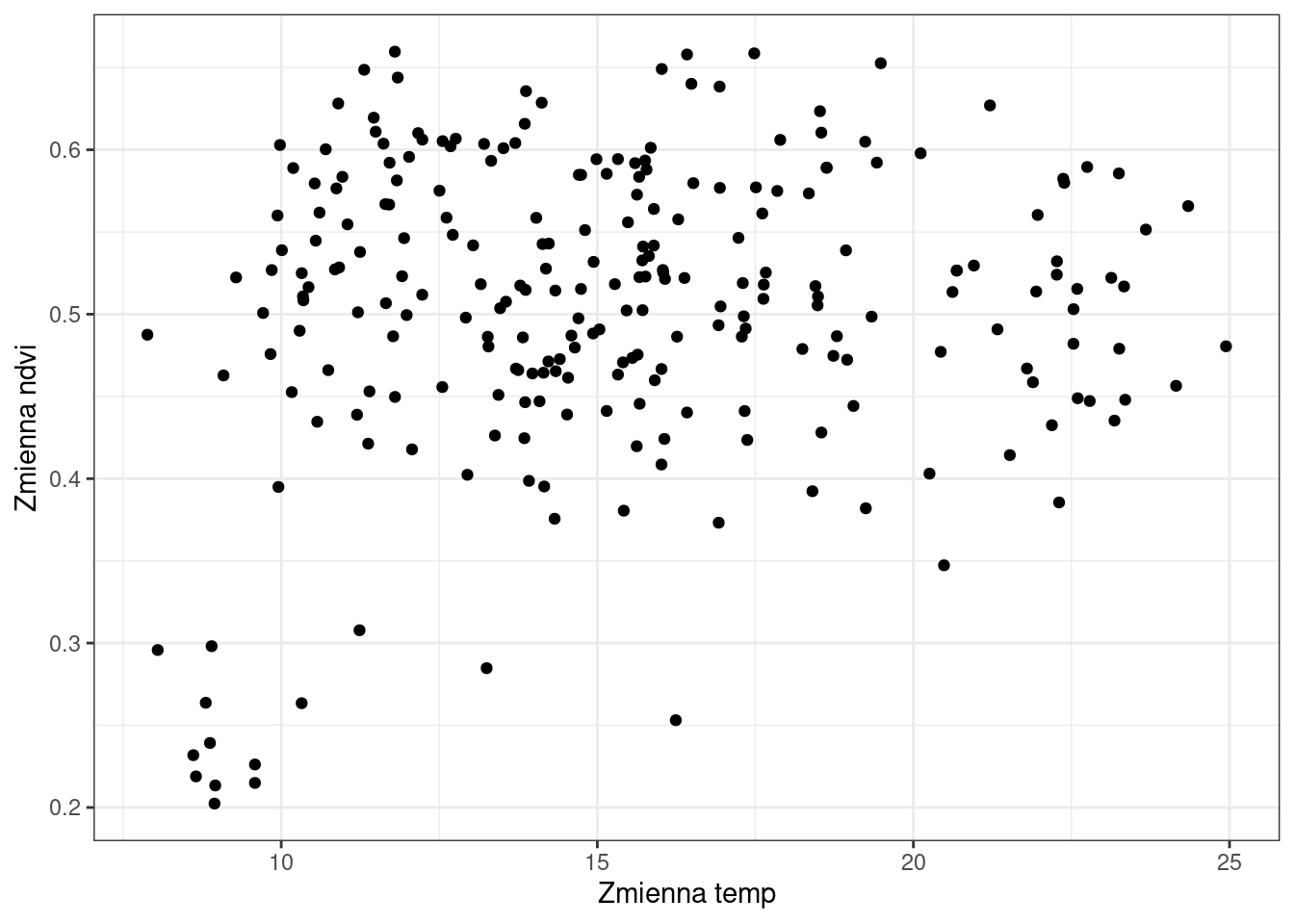

Czy istnieje zależność między zmienną temp, a ndvi?

ggplot(punkty, aes(temp, srtm)) +
  geom_point() +
  labs(x = "Zmienna temp", y = "Zmienna srtm") + 
  theme_bw()

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).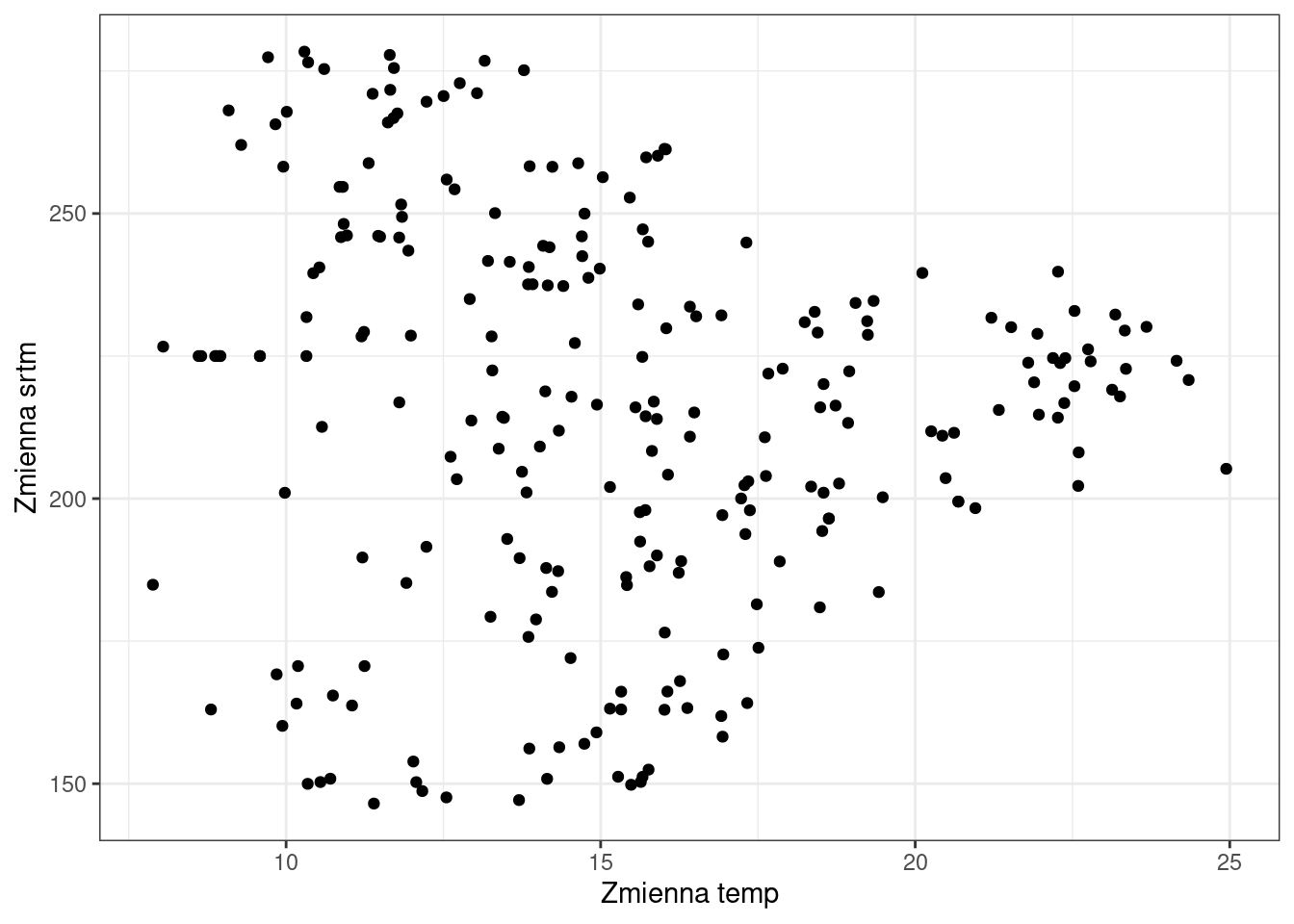

Czy istnieje zależność między zmienną temp, a srtm?

Do liczbowego określenia zależności między zmiennymi wykorzystano test korelacji dla współczynnika korelacji rang Spearmana. Test korelacji wyliczany jest z wykorzystaniem funkcji cor.test(), w której jako metodę (argument method) można podać współczynnik korelacji rang Spearmana (method = “spearman”) lub współczynnik korelacji liniowej Pearsona (method = “pearson”). W wyniku otrzymamy wartość współczynnika korelacji oraz poziom istotności.

cor.test(punkty$temp, punkty$ndvi, method = "spearman")

Warning in cor.test.default(punkty$temp, punkty$ndvi, method = "spearman"):
Cannot compute exact p-value with ties


    Spearman's rank correlation rho

data:  punkty$temp and punkty$ndvi
S = 2378524, p-value = 0.4074
alternative hypothesis: true rho is not equal to 0
sample estimates:
       rho 
0.05294538

cor.test(punkty$temp, punkty$srtm, method = "spearman")

Warning in cor.test.default(punkty$temp, punkty$srtm, method = "spearman"):
Cannot compute exact p-value with ties


    Spearman's rank correlation rho

data:  punkty$temp and punkty$srtm
S = 2866567, p-value = 0.00782
alternative hypothesis: true rho is not equal to 0
sample estimates:
       rho 
-0.1695597

Jaka jest wartość korelacji dla zmiennych temp/ndvi, oraz temp/srtm? Czy w każdym z przypadków uzyskano wynik istotny statystycznie?

Zmienność temperatury w klasach pokrycia terenu

Zależność między zmienną ilościową a jakościową można przedstawić na wykresie pudełkowym.

punkty$clc = as.factor(punkty$clc)
ggplot(punkty, aes(x = clc, y = temp)) + 
  geom_boxplot() + 
  labs(x = "Zmienna clc", y = "Zmienna temp") + 
  theme_bw()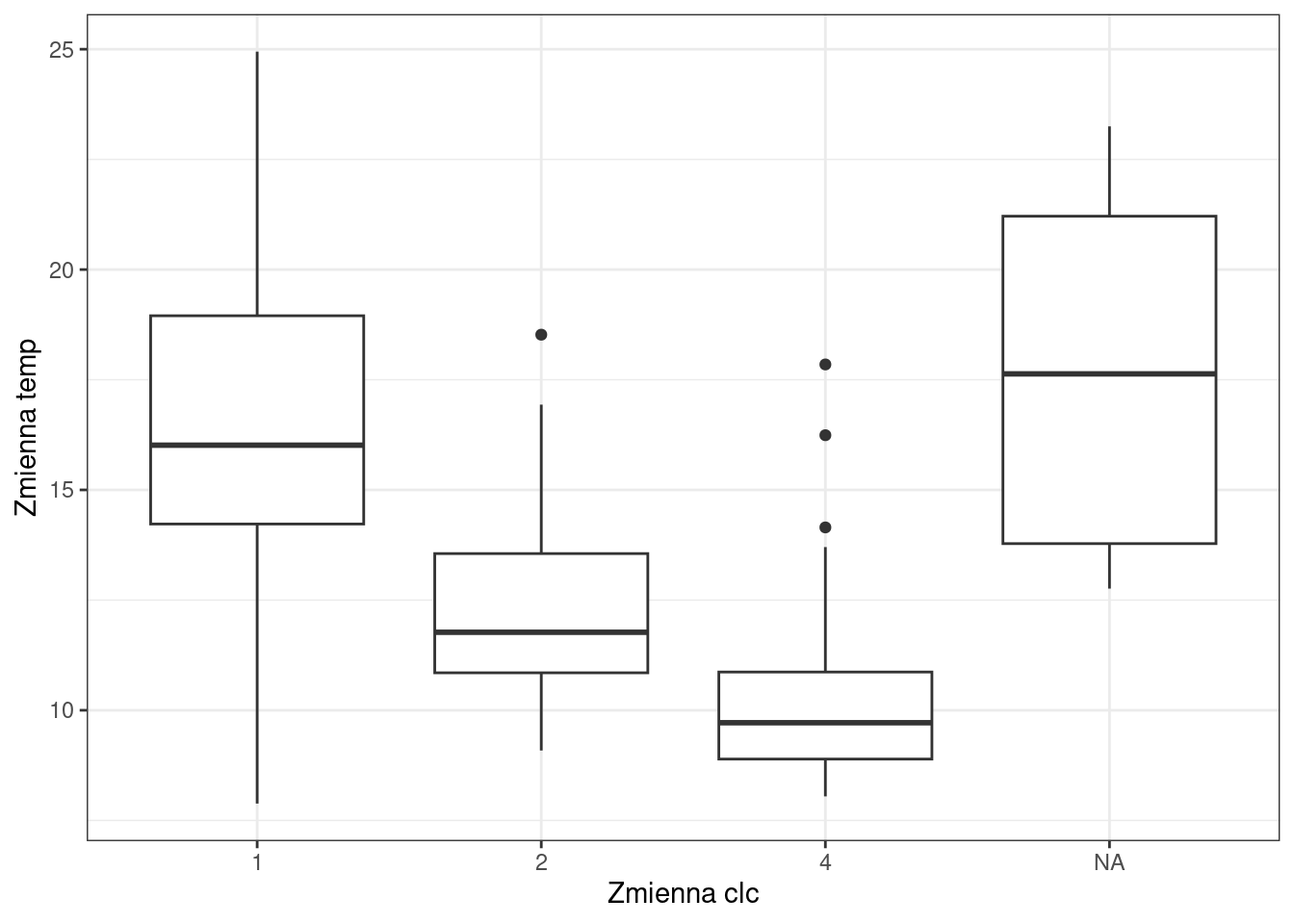

Czy temperatura różnicuje się w zależności od klasy pokrycia terenu?

Do określenia istotności różnić średniej pomiędzy grupami można wykorzystać analizę wariancji. Analiza wariancji (ang. Analysis of Variance - ANOVA) służy do testowania istotności różnic między średnimi w wielu grupach. Metoda ta służy do oceny czy średnie wartości cechy Y różnią się istotnie pomiędzy grupami wyznaczonymi przez zmienną X.

aov_test = aov(temp ~ clc, data = punkty)
summary(aov_test)

             Df Sum Sq Mean Sq F value Pr(>F)    
clc           2   1272   636.0   60.86 <2e-16 ***
Residuals   239   2498    10.4                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
5 observations deleted due to missingness

ANOVA nie pozwala natomiast na stwierdzenie między którymi grupami występują różnice. Aby to stwierdzić konieczne jest wykonanie porównań wielokrotnych (post-hoc), np. testu Tukeya.

tukey = TukeyHSD(aov_test, "clc")
plot(tukey, las = 1)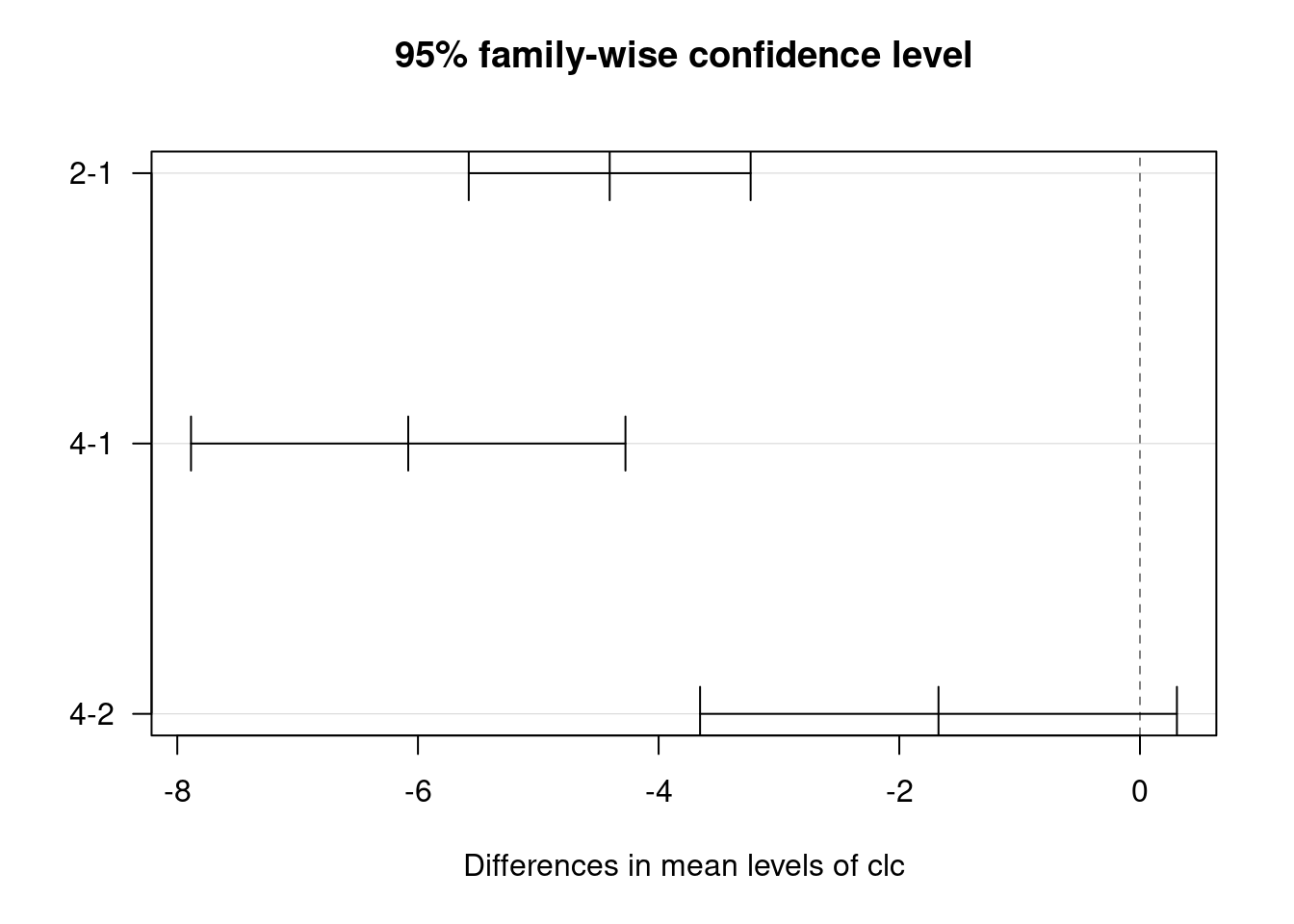

Czy temperatura różnicuje się istotnie w zależności od klasy pokrycia terenu?

3.3 Eksploracyjna przestrzenna analiza danych

Do sprawdzenia poprawności współrzędnych, określenia typu próbkowania oraz identyfikacji danych odstających lokalnie można wykorzystać mapę lokalizacyjną pokazującą lokalizację wykonania pomiarów. Mapę lokalizacyjną można wykonać wykorzystując pakiet tmap.

3.3.1 Sprawdzenie poprawności współrzędnych oraz określenie typu próbkowania

Czy współrzędne są w odpowiednim porządku (X-Y, Y-X)?
Czy współrzędne są w odpowiednim układzie?
Czy wszystkie punkty znajdują się na badanym obszarze?

tm_shape(granica) +
        tm_polygons() +
        tm_shape(punkty) +
        tm_symbols() +
        tm_grid()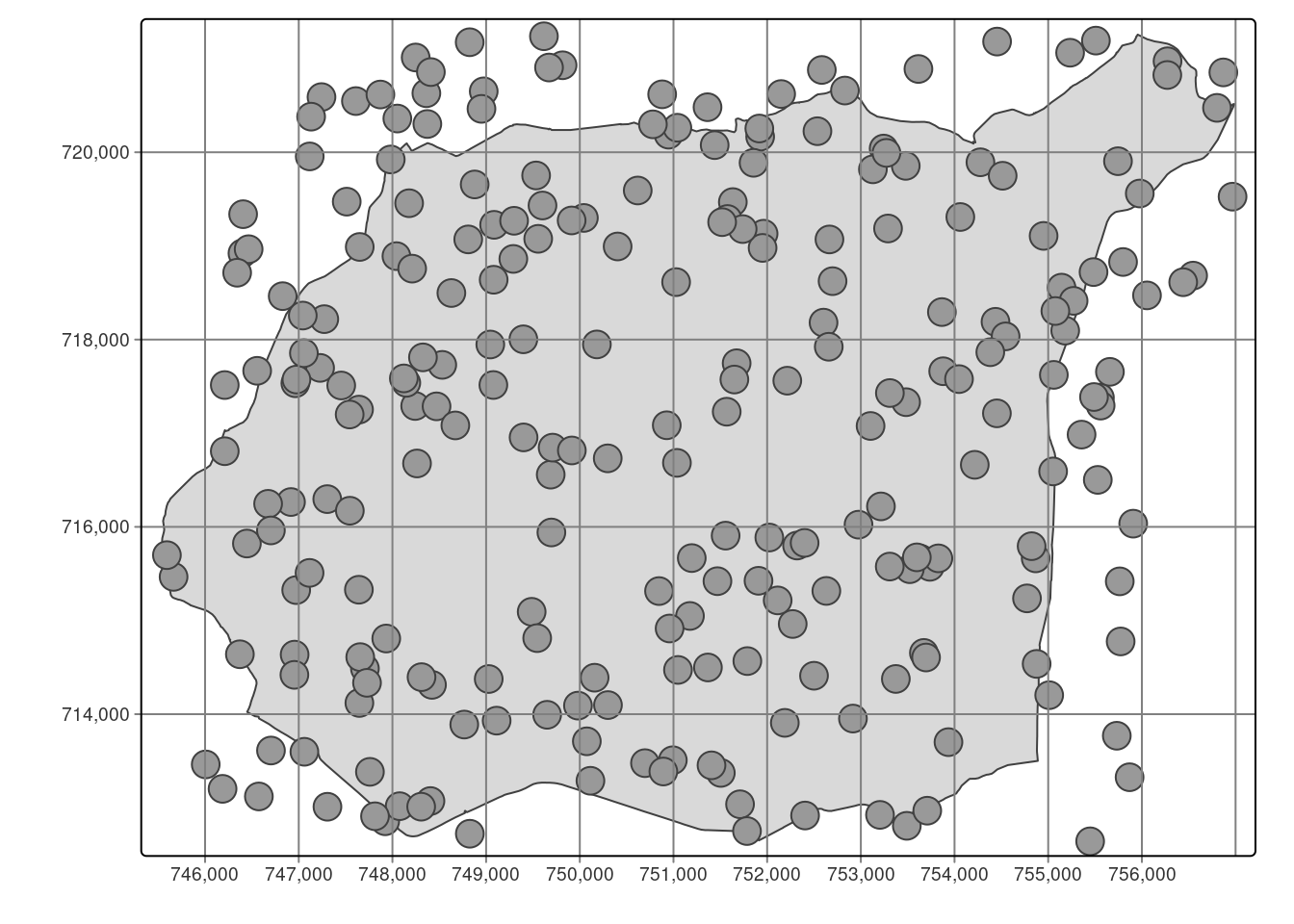

Sprawdzenie poprawności danych oraz identyfikacja danych odstających lokalnie

tm_shape(punkty) +
  tm_graticules(labels.show = FALSE) +
  tm_symbols(col = "temp",
             style = "cont", 
             n = 10,
             palette = "-Spectral",
             title.col = "Zmienna temp")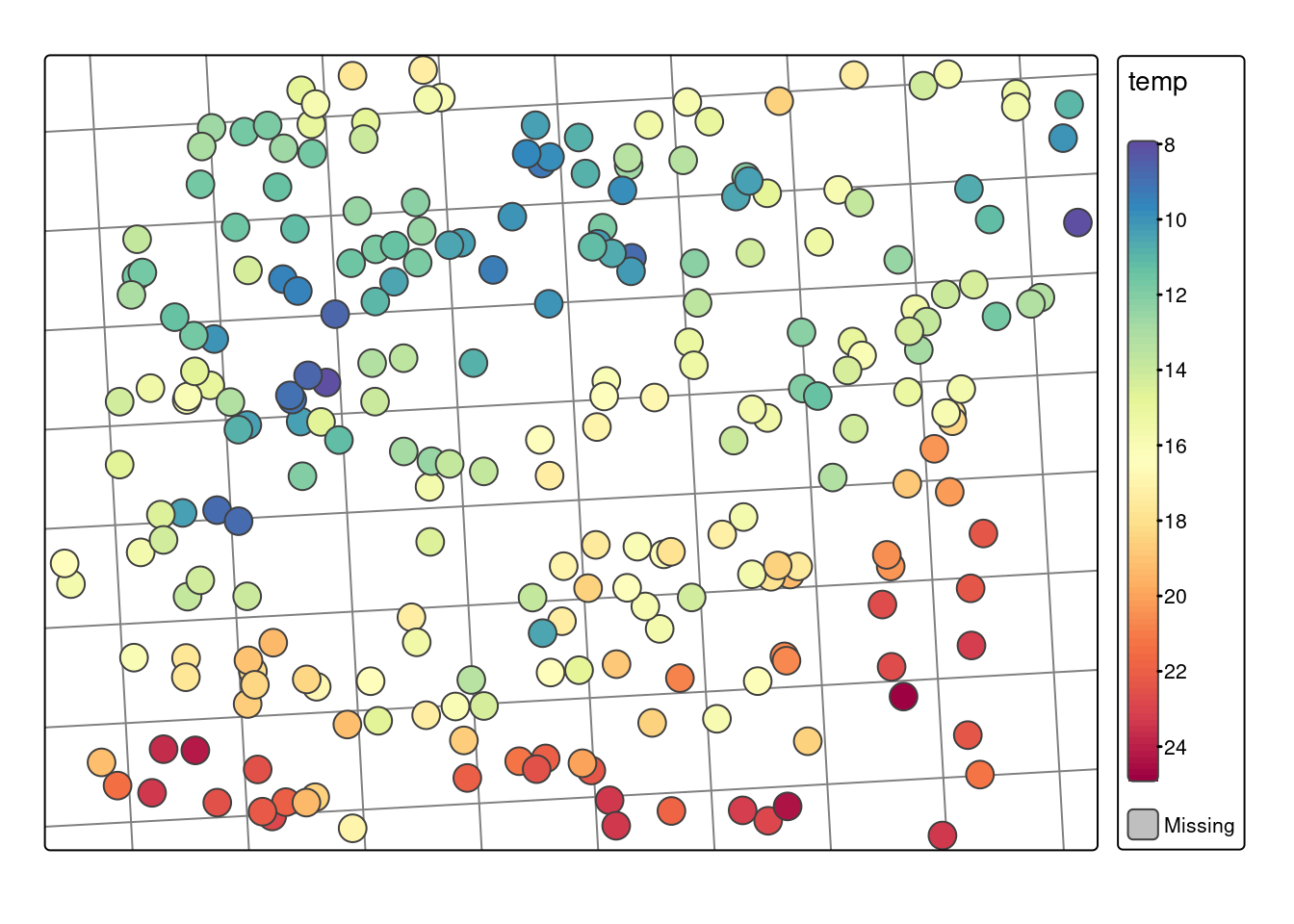

Rozkład wartości temperatury powietrza w analizowanym obszarze.

4 Przykład 2: Analiza przestępczości w hrabstwie Cook

4.1 Dane

Plik socio_economic_variables.gpkg dostarcza danych społeczno-ekonomicznych dla obszaru hrabstwa Cook (centralna część miasta Chicago). Dane te pochodzą ze zbioru danych American Community Survey: ACS 2016-2020.
Plik crimes_vehicle_theft.gpkg zawiera lokalizacje przestępstw (kradzieży samochodów) dla centralnej części Chicago dla 2020 roku.

socio_data = read_sf("data/socio_economic_variables.gpkg")
crimes = read_sf("data/crimes_vehicle_theft.gpkg")

tm_shape(socio_data) + 
  tm_borders(col = "grey") + 
tm_shape(crimes) +
  tm_dots(fill = "red")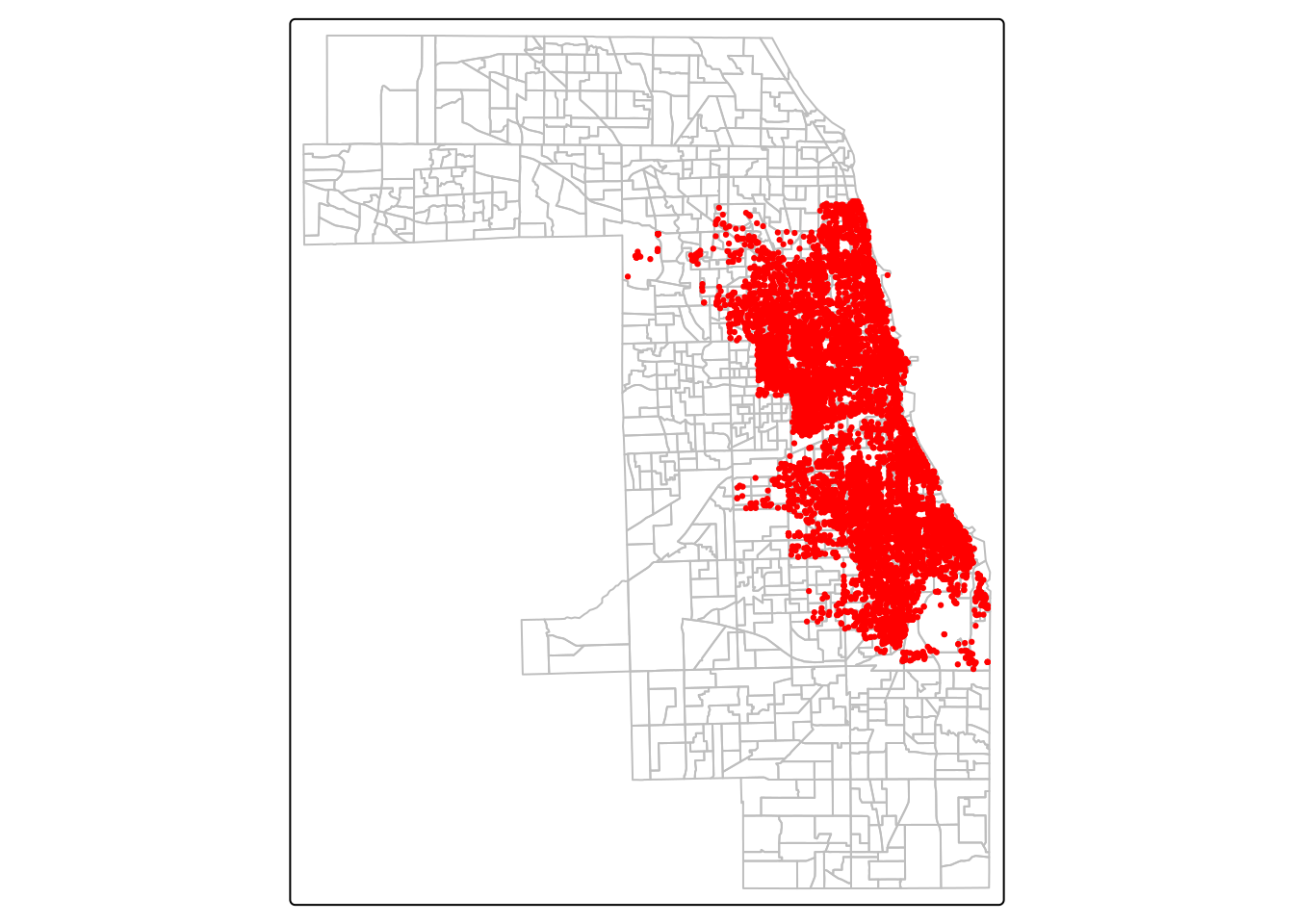

Kolorem czerwonym zaznaczono lokalizacje przestępstw (kradzieży samochodów), a szarym granice obszarów spisowych w hrabstwie Cook, dla których pozyskano dane ekonomiczne.

Wykorzystując funkcję str() możemy uzyskać podstawowe informacje o analizowanych zmiennych.

str(socio_data)

sf [1,332 × 23] (S3: sf/tbl_df/tbl/data.frame)
 $ GEOID            : chr [1:1332] "17031822400" "17031740100" "17031530501" "17031830300" ...
 $ POP              : num [1:1332] 6214 2962 5073 4536 2523 ...
 $ WHITE            : num [1:1332] 0.6999 0.8383 0.0195 0.2277 0.8922 ...
 $ BLACK            : num [1:1332] 0.00724 0 0.94067 0.74757 0.04201 ...
 $ ASIAN            : num [1:1332] 0.0439 0.0135 0 0.0117 0.0103 ...
 $ HISPANIC         : num [1:1332] 0.242 0.1435 0.0264 0.0126 0.0289 ...
 $ FOREIGN_BORN     : num [1:1332] 0.2948 0.023 0.0199 0.0423 0.0258 ...
 $ UNEMPL           : num [1:1332] 0.0339 0.0554 0.2593 0.1521 0.0249 ...
 $ PUBLIC_ASSIST    : num [1:1332] 0.1664 0.0565 0.4314 0.183 0.0387 ...
 $ VACANT           : num [1:1332] 0.1591 0.0884 0.2364 0.1074 0.0459 ...
 $ OCCUPIED         : num [1:1332] 1 1 1 1 1 ...
 $ OWNER            : num [1:1332] 0.662 0.851 0.567 0.416 0.828 ...
 $ RENTER           : num [1:1332] 0.338 0.149 0.433 0.584 0.172 ...
 $ MEDIAN_INCOME    : num [1:1332] 51782 84800 45651 48491 102543 ...
 $ MEDIAN_BUILT_YEAR: num [1:1332] 1972 1954 0 1958 1947 ...
 $ MEDIAN_HOME_VALUE: num [1:1332] 204900 245200 121100 26000 285700 ...
 $ OTHER            : num [1:1332] 0.993 0.995 0.987 1 0.973 ...
 $ SEX_RATIO        : num [1:1332] 0.000974 0.001032 0.0008 0.000715 0.000941 ...
 $ EDU_HIGH         : num [1:1332] 0.209 0.33 0.142 0.321 0.619 ...
 $ HOME_VALUES_CAT  : chr [1:1332] "medium" "medium" "low" "low" ...
 $ INCOME_CAT       : chr [1:1332] "medium" "medium" "low" "medium" ...
 $ BUILT_YEAR_CAT   : chr [1:1332] "medium" "medium" "old" "medium" ...
 $ geom             :sfc_MULTIPOLYGON of length 1332; first list element: List of 1
  ..$ :List of 1
  .. ..$ : num [1:37, 1:2] -87.8 -87.8 -87.8 -87.8 -87.8 ...
  ..- attr(*, "class")= chr [1:3] "XY" "MULTIPOLYGON" "sfg"
 - attr(*, "sf_column")= chr "geom"
 - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA NA NA NA NA NA NA ...
  ..- attr(*, "names")= chr [1:22] "GEOID" "POP" "WHITE" "BLACK" ...

Ramka danych socio_data zawiera szereg zmiennych społeczno-ekonomicznych i demograficznych:

liczbę ludności w każdym obszarze spisowym (POP)
odsetek ludności w podziale na grupy rasowo-etniczne (WHITE, BLACK, ASIAN, HISPANIC, OTHER)
odsetek osób urodzonych za granicą (FOREIGN_BORN)
odsetek osób bezrobotnych (UNEMPL)
odsetek osób korzystających z pomocy społecznej (PUBLIC_ASSIST)
odsetek niezamieszkłaych domów oraz mieszkań (VACANT)
odsetek zamieszkałych domów oraz mieszkań (OCCUPPIED)
odsetek domów/mieszkań zamieszkałych przez właściciela (OWNER)
odsetek domów/mieszkań zamieszkałych przez osoby wynajmujące (RENTER)
mediana dochodów w obszarze spisowym (MEDIAN_INCOME)
mediana wieku zabudowy w obszarze spisowym (MEDIAN_BUILT_YEAR)
mediana wartości domów w obszarze spisowym (MEDIAN_HOME_VALUE)
odsetek osób w wyższym wykształceniem (EDU_HIGH)
wartość domów: niska, średnia, wysoka (HOME_VALUES_CAT)
dochód: niski, średni, wysoki (INCOME_CAT)
wiek zabudowy: nowa, średnia, stara zabudowa (BUILT_YEAR_CAT)

4.2 Cel analizy

Celem analizy jest znalezienie czynników społeczno-ekonomicznych wpływających na poziom przestępczości (kradzieży samochodów). Czy istnieje zależność między poziomem przestępczości, a zmiennymi społeczno-ekonomicznymi?

4.3 Przygotowanie danych do analizy

Ujednolicenie układów współrzędnych między warstwami.

Lokalizacja przestępstw jest w układzie WGS84, warstwę trzeba przekształcić do układu warstwy z danymi społeczno-ekonomicznymi.

crimes = st_transform(crimes, st_crs(socio_data))

selekcja obszarow spisowych, w których zlokalizowane są przestępstwa.

socio_data = socio_data[crimes, ]

zliczenie przestępstw w obszarach spisowych

socio_data$NB_CRIMES <- lengths(st_intersects(socio_data, crimes))

obliczenie odsetka przestępst na 1000 mieszkańców (ang. crime rates)

socio_data$CRIME_RATE = (socio_data$NB_CRIMES/socio_data$POP)*1000

utworzenie ramki danych bez kolumny z geometrią (będzie potrzebne przy części analiz statystycznych)

socio_data_attr = socio_data
socio_data_attr$geom <-NULL

4.4 Eksploracyjna nieprzestrzenna analiza danych

Podsumowanie numeryczne

summary(socio_data_attr)

    GEOID                POP            WHITE             BLACK        
 Length:788         Min.   :    0   Min.   :0.00000   Min.   :0.00000  
 Class :character   1st Qu.: 2044   1st Qu.:0.03004   1st Qu.:0.02311  
 Mode  :character   Median : 3142   Median :0.22915   Median :0.09334  
                    Mean   : 3440   Mean   :0.30523   Mean   :0.34852  
                    3rd Qu.: 4570   3rd Qu.:0.57202   3rd Qu.:0.81515  
                    Max.   :10974   Max.   :0.92883   Max.   :1.00000  
                                    NA's   :3         NA's   :3        
     ASIAN            HISPANIC        FOREIGN_BORN        UNEMPL       
 Min.   :0.00000   Min.   :0.00000   Min.   :0.0000   Min.   :0.00000  
 1st Qu.:0.00000   1st Qu.:0.04447   1st Qu.:0.0458   1st Qu.:0.03864  
 Median :0.02261   Median :0.13664   Median :0.1531   Median :0.07256  
 Mean   :0.06003   Mean   :0.26169   Mean   :0.1803   Mean   :0.09981  
 3rd Qu.:0.07913   3rd Qu.:0.40534   3rd Qu.:0.2974   3rd Qu.:0.14334  
 Max.   :0.84913   Max.   :0.98900   Max.   :0.6585   Max.   :0.46776  
 NA's   :3         NA's   :3         NA's   :3        NA's   :3        
 PUBLIC_ASSIST         VACANT           OCCUPIED          OWNER       
 Min.   :0.00000   Min.   :0.00000   Min.   :0.9983   Min.   :0.0000  
 1st Qu.:0.07705   1st Qu.:0.06515   1st Qu.:0.9998   1st Qu.:0.2993  
 Median :0.17330   Median :0.09682   Median :0.9999   Median :0.4352  
 Mean   :0.21870   Mean   :0.11825   Mean   :0.9999   Mean   :0.4516  
 3rd Qu.:0.33914   3rd Qu.:0.14966   3rd Qu.:1.0000   3rd Qu.:0.5860  
 Max.   :0.77024   Max.   :0.47222   Max.   :1.0000   Max.   :0.9745  
 NA's   :3         NA's   :3         NA's   :3        NA's   :3       
     RENTER        MEDIAN_INCOME    MEDIAN_BUILT_YEAR MEDIAN_HOME_VALUE
 Min.   :0.02548   Min.   : 12328   Min.   :   0      Min.   :  65500  
 1st Qu.:0.41399   1st Qu.: 38394   1st Qu.:   0      1st Qu.: 168600  
 Median :0.56484   Median : 55062   Median :1945      Median : 248700  
 Mean   :0.54843   Mean   : 63882   Mean   :1148      Mean   : 288966  
 3rd Qu.:0.70067   3rd Qu.: 80872   3rd Qu.:1957      3rd Qu.: 368300  
 Max.   :1.00000   Max.   :216667   Max.   :2006      Max.   :1245500  
 NA's   :3         NA's   :8        NA's   :3         NA's   :19       
     OTHER          SEX_RATIO            EDU_HIGH       HOME_VALUES_CAT   
 Min.   :0.8020   Min.   :0.0004454   Min.   :0.01092   Length:788        
 1st Qu.:0.9636   1st Qu.:0.0008190   1st Qu.:0.15302   Class :character  
 Median :0.9821   Median :0.0009405   Median :0.30406   Mode  :character  
 Mean   :0.9755   Mean   :0.0009558   Mean   :0.38004                     
 3rd Qu.:0.9960   3rd Qu.:0.0010612   3rd Qu.:0.59072                     
 Max.   :1.0000   Max.   :0.0088278   Max.   :0.93945                     
 NA's   :3        NA's   :3           NA's   :3                           
  INCOME_CAT        BUILT_YEAR_CAT       NB_CRIMES       CRIME_RATE    
 Length:788         Length:788         Min.   : 1.00   Min.   :0.1563  
 Class :character   Class :character   1st Qu.: 5.00   1st Qu.:1.5722  
 Mode  :character   Mode  :character   Median : 9.00   Median :2.9283  
                                       Mean   :12.53   Mean   :   Inf  
                                       3rd Qu.:16.00   3rd Qu.:6.1173  
                                       Max.   :92.00   Max.   :   Inf

table(socio_data_attr$INCOME_CAT)


  high    low medium 
   151    282    347

table(socio_data_attr$HOME_VALUES_CAT)


  high    low medium 
   207    198    364

table(socio_data_attr$BUILT_YEAR_CAT)


medium    new    old 
   312     16    457

4.4.1 Rozkład danych o przestępczości

ggplot(socio_data_attr, aes(x = CRIME_RATE)) + geom_histogram() + theme_bw()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Warning: Removed 3 rows containing non-finite outside the scale range
(`stat_bin()`).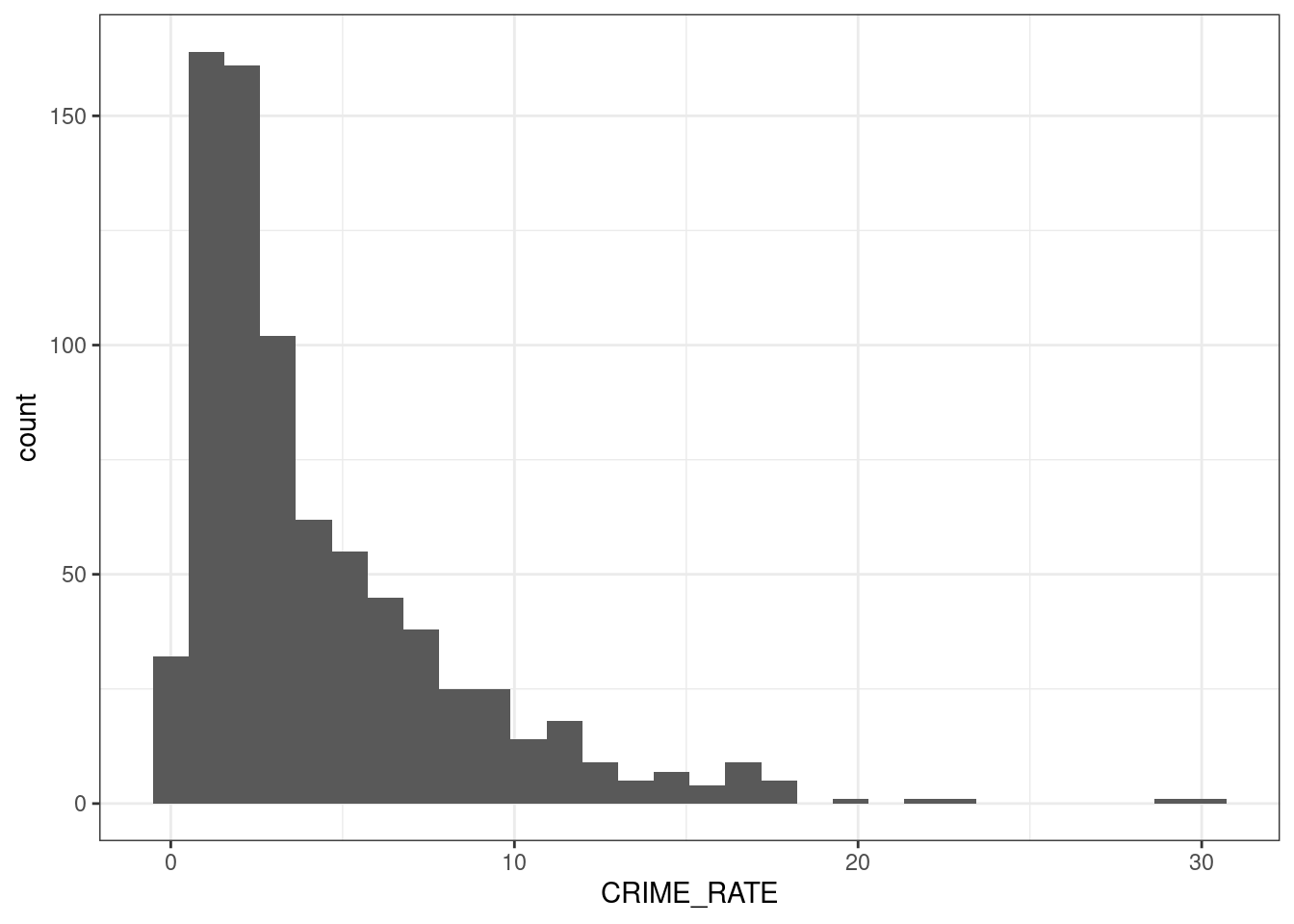

4.4.2 Zależność między odsetkiem przestępstw a zmiennymi społeczno-ekonomicznymi

cor = cor(socio_data_attr[24], socio_data_attr[3:19], method = "spearman", use = "complete.obs")
round(cor, 2)

           WHITE BLACK ASIAN HISPANIC FOREIGN_BORN UNEMPL PUBLIC_ASSIST VACANT
CRIME_RATE -0.58  0.64 -0.49    -0.41        -0.54   0.48          0.55   0.53
           OCCUPIED OWNER RENTER MEDIAN_INCOME MEDIAN_BUILT_YEAR
CRIME_RATE    -0.54 -0.35   0.35          -0.5             -0.01
           MEDIAN_HOME_VALUE OTHER SEX_RATIO EDU_HIGH
CRIME_RATE             -0.41  0.15     -0.26    -0.37

W kolejnym kroku zostaną wyselekcjonowane wartości współczynnika korelacji +/- 0,5, a następnie dla nich zostaną wykonane wykresy rozrzutu.

cor_v = as.vector(cor)
names(cor_v) = colnames(cor)
sel_cor = cor_v[abs(cor)>0.5]
round(sel_cor, 2)

        WHITE         BLACK  FOREIGN_BORN PUBLIC_ASSIST        VACANT 
        -0.58          0.64         -0.54          0.55          0.53 
     OCCUPIED 
        -0.54

Objaśnienie zmiennych:

- WHITE - odsetek ludności białych
- BLACK - odsetek ludności czarnej 
- FOREIGN_BORN - odsetek ludności urodzonej zagranicą
- PUBLIC ASSIST - odestek gospodarstw domowych korzystających z pomocy społecznej
- VACANT - odsetek niezamieszkałych budynków
- OCCUPIED - odsetek zamieszkałych budynków

Wizualizacja zależności między zmiennymi ze współczynnikiem korelacji +/- 0,5.

library(PerformanceAnalytics)
list_variables = names(sel_cor)
chart.Correlation(socio_data_attr[, c("CRIME_RATE", list_variables)], histogram=TRUE, pch=19, method = "spearman")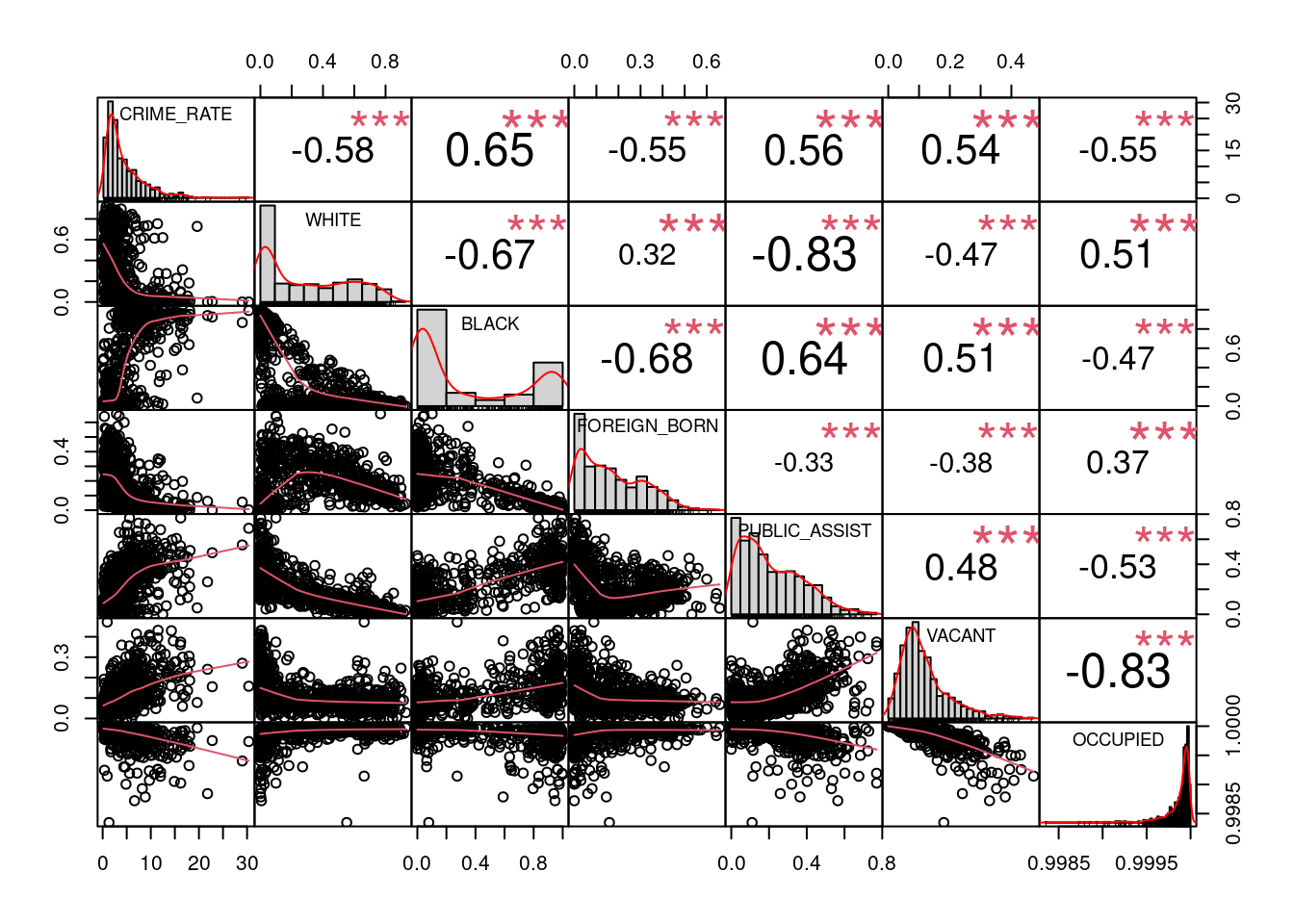

4.4.3 Zmienność odsetka przestępczości w klasach poziomu dochodu, cen domów oraz wieku zabudowy

Zależność między odsetkiem przestępczości a poziomem dochodów.

Wyróżniono 3 klasy używając zmiennej MEDIAN_INCOME:

low - wartości dochodów niższe od kwartyla 1.
medium - wartości dochodów między 1 i 3 kwartylem.
high - wartości dochodów wyższe do 3. kwartyla.

library(dplyr)
socio_data_attr %>% na.omit() %>%  
  mutate(INCOME_CAT = factor(INCOME_CAT,level=c("low", "medium", "high"))) %>% 
ggplot(., aes(x = INCOME_CAT, y = CRIME_RATE)) + 
  geom_boxplot()  + 
  xlab("Household income") + ylab("Crime rates") + 
  theme_bw()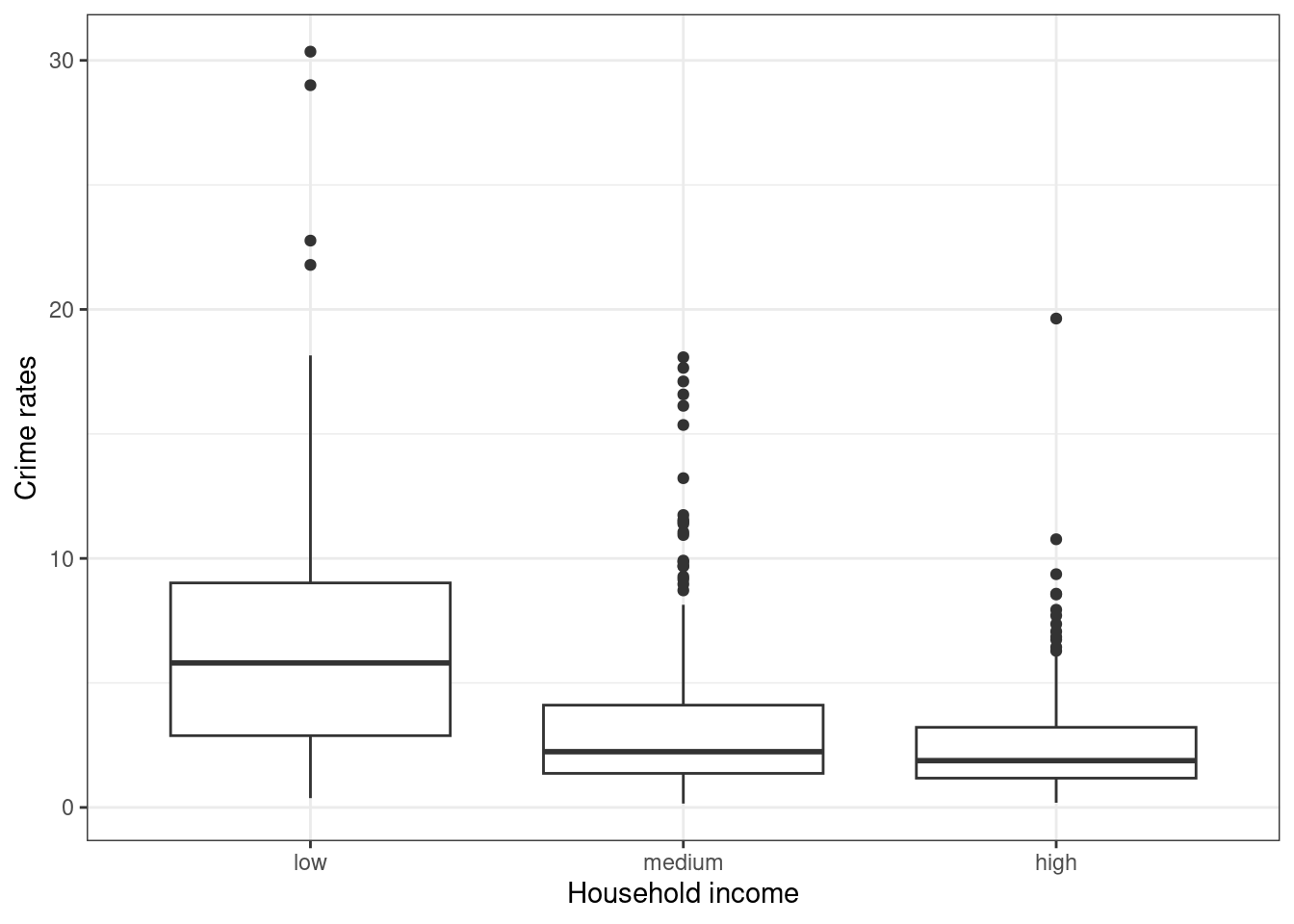

Zależność między odsetkiem przestępczości a cenami domów.

Wyróżniono 3 klasy używając zmiennej MEDIAN_HOME_VALUE:

low - wartości cen domów niższe od kwartyla 1.
medium - wartości cen domów między 1 i 3 kwartylem.
high - wartości cen domów wyższe do 3. kwartyla.

socio_data_attr %>% na.omit() %>%  
  mutate(HOME_VALUES_CAT = factor(HOME_VALUES_CAT,level=c("low", "medium", "high"))) %>% 
ggplot(., aes(x = HOME_VALUES_CAT, y = CRIME_RATE)) + 
  geom_boxplot()  + 
  xlab("Home values") + ylab("Crime rates") + 
  theme_bw()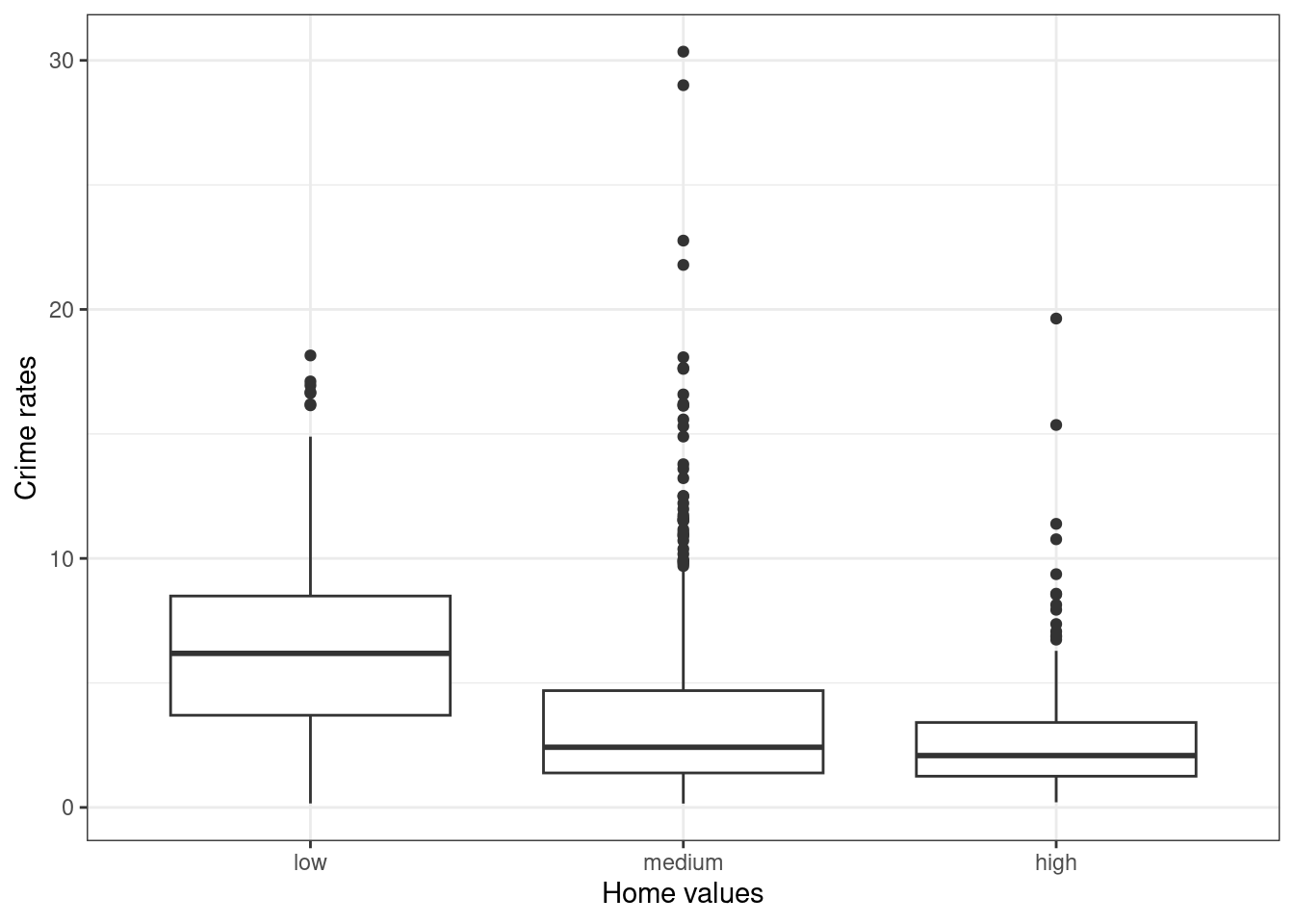

Zależnośc między odsetkiem przestęczpości, a wiekiem zabudowy.

Wyróżnione zostały 3 klasy zabudowy:

old - wybudowane przed 1950,
medium - wybudowane między 1950 a 2000,
new - wybudowane po 2000.

socio_data_attr %>% na.omit() %>%  
  mutate(BUILT_YEAR_CAT = factor(BUILT_YEAR_CAT,level=c("old", "medium", "new"))) %>% 
ggplot(., aes(x = BUILT_YEAR_CAT, y = CRIME_RATE)) + 
  geom_boxplot()  + 
  xlab("Housing age") + ylab("Crime rates") + 
  theme_bw()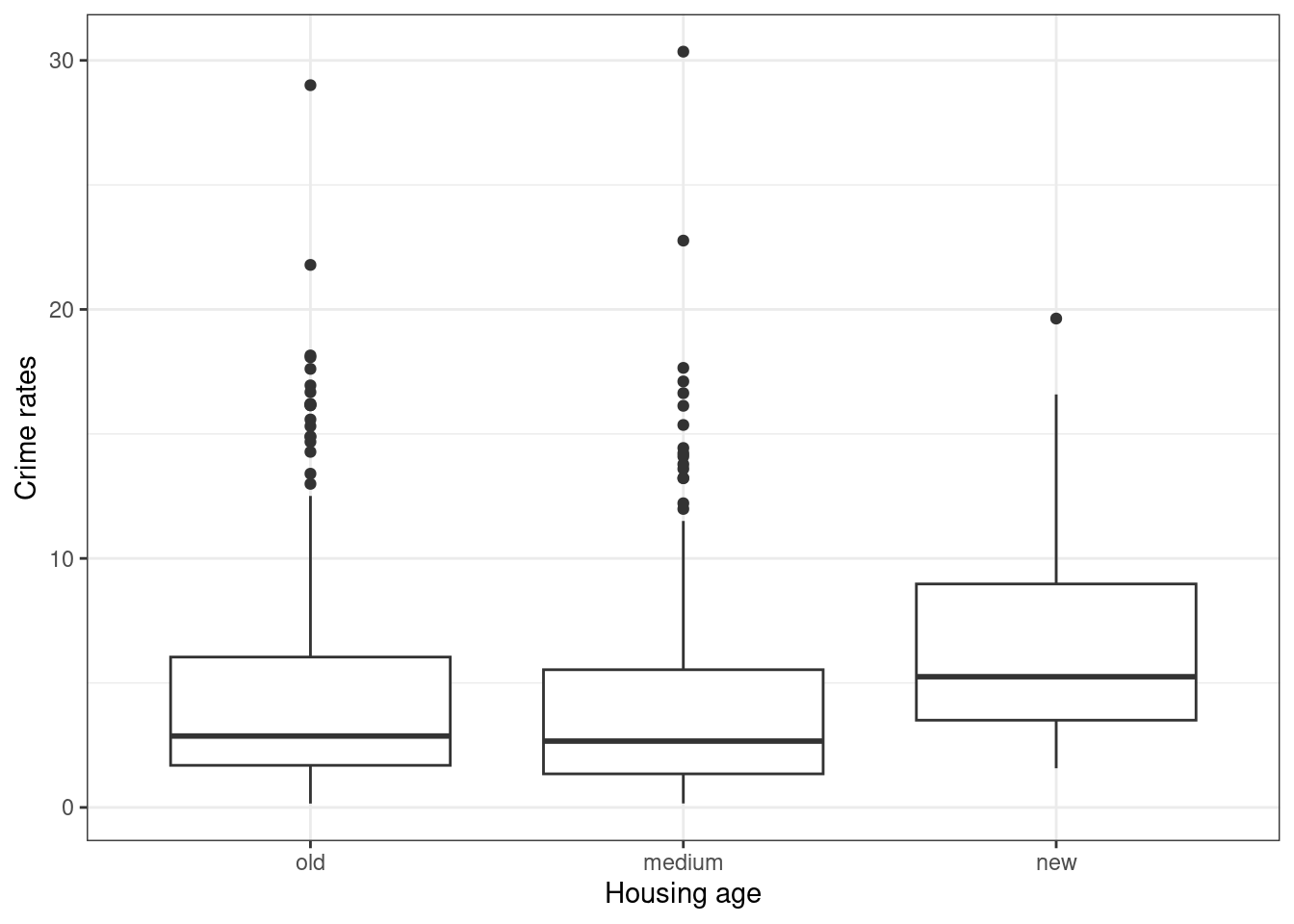

4.5 Eksploracyjna przestrzenna analiza danych

Eksploracyjna przestrzenna analiza danych obejmuje przede wszystkim wizualizację zmiennych społeczno-ekonomicznych oraz odsetka przestępczości w celu wizualnego określenia, czy istnieją obszary o wysokim/niskim odsetku przestępczości i czy są one powiązane z wyższymi/niższymi wartościami zmiennych społeczno-ekonomicznych.

Wizualizacja danych ma także na celu sprawdzenie poprawności danych, w tym między innymi identyfikacja danych odstających lokalnie.

4.5.1 Odsetek przestępczości

tm_shape(socio_data) + 
  tm_polygons(fill = "CRIME_RATE", palette = "YlOrRd", n = 4, style = 'jenks')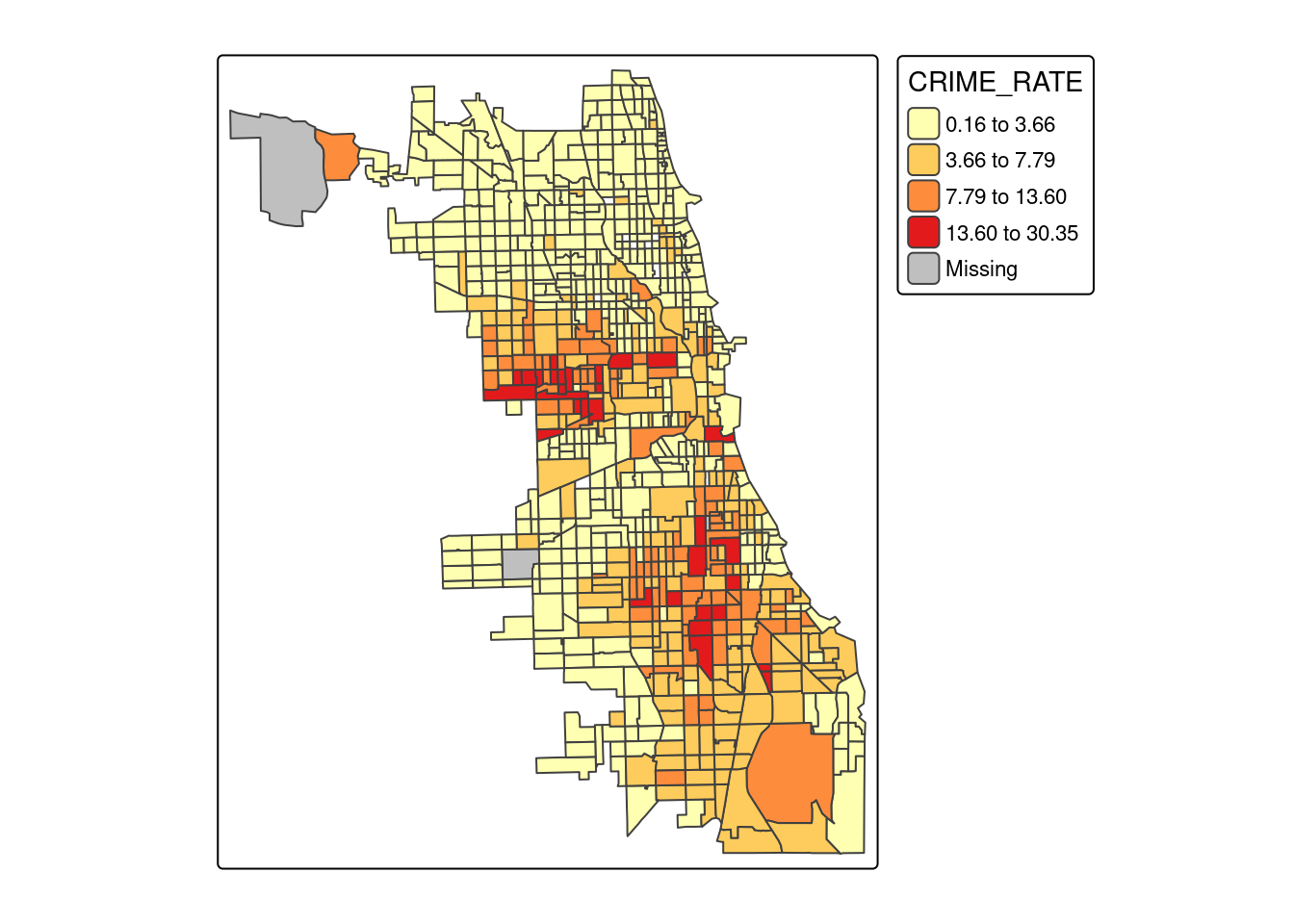

4.5.2 Struktura rasowo-etniczna ludności

tm_shape(socio_data) + 
  tm_polygons(fill = "WHITE", palette = "YlOrRd")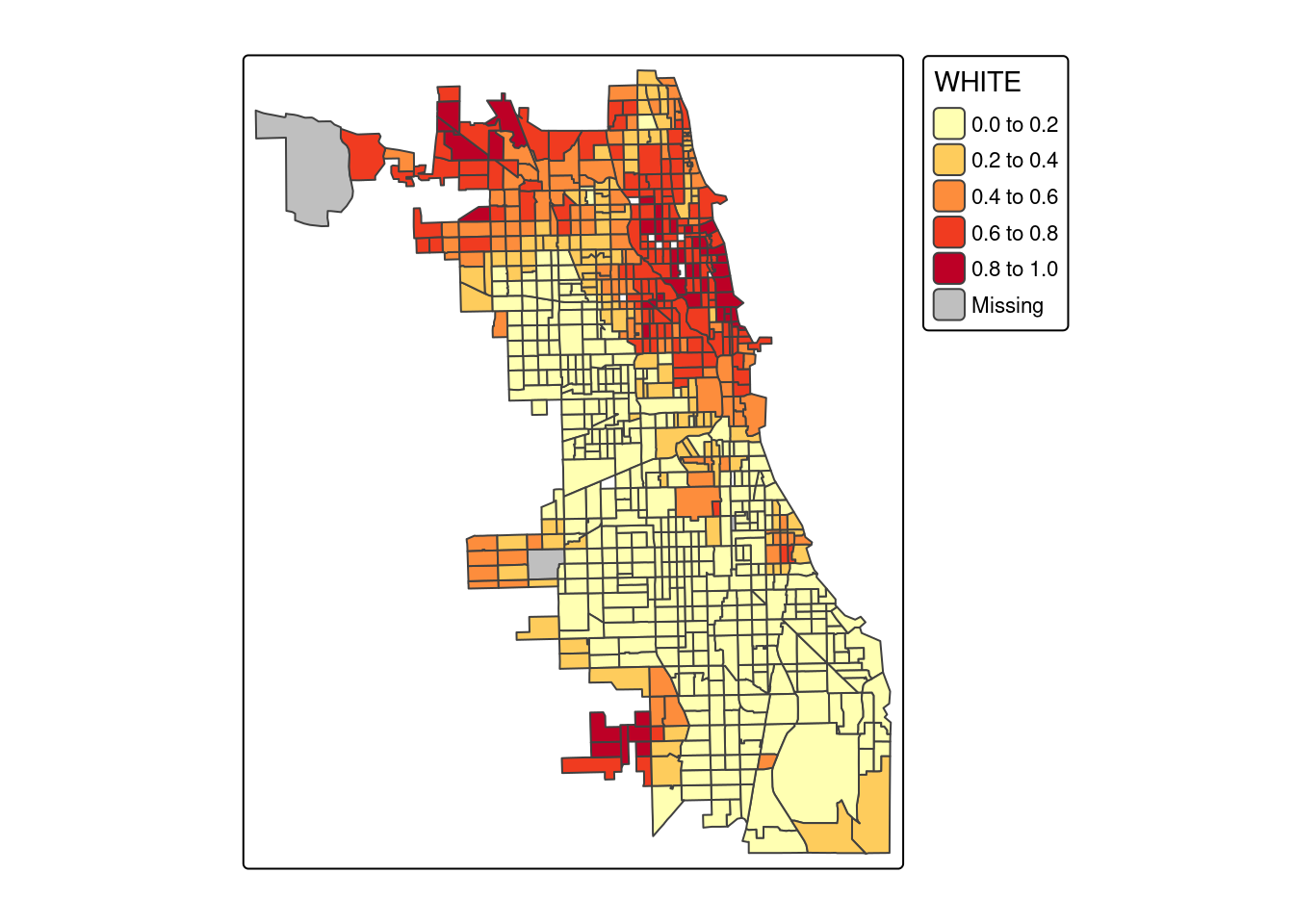

tm_shape(socio_data) + 
  tm_polygons(fill = "BLACK", palette = "YlOrRd")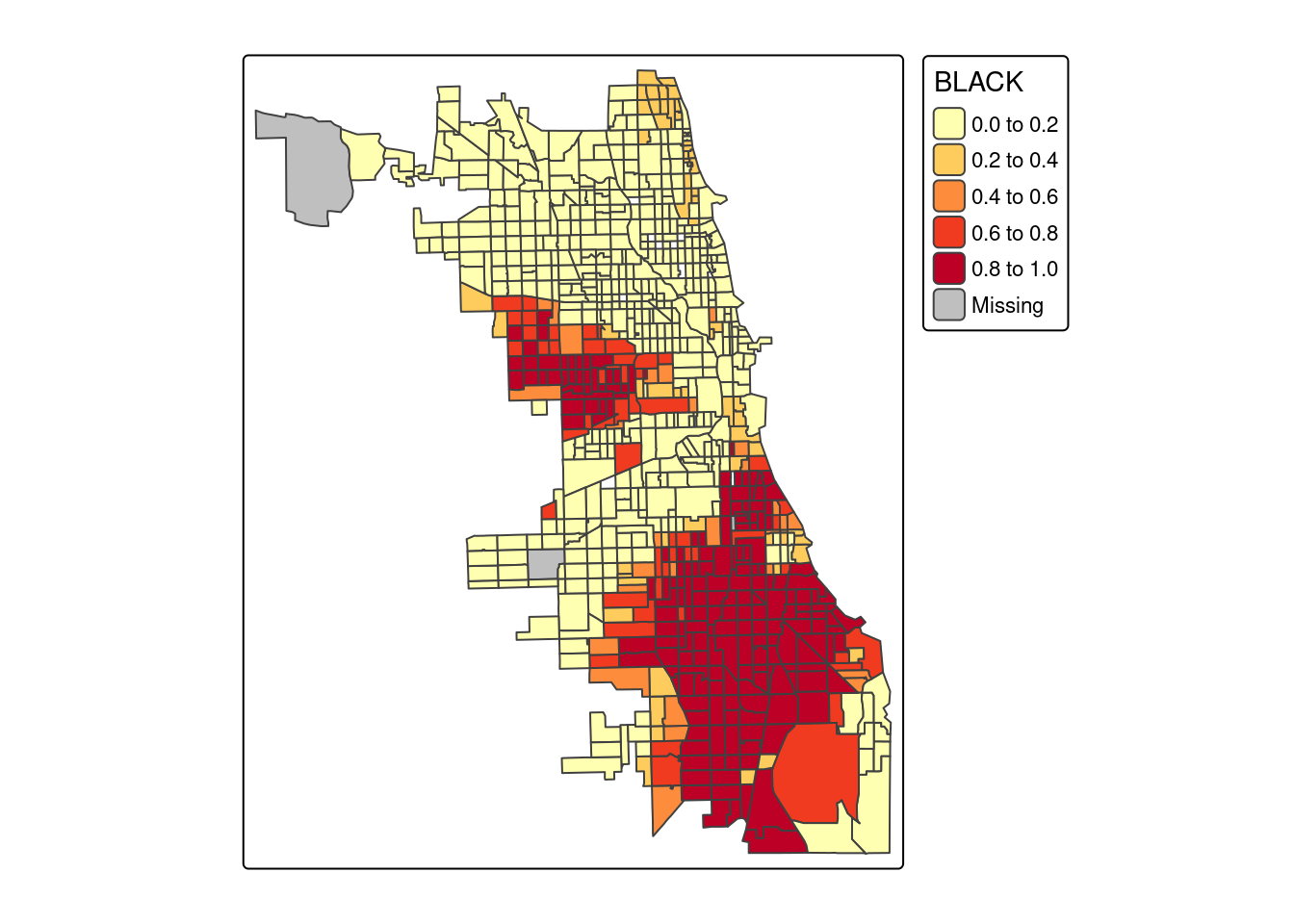

tm_shape(socio_data) + 
  tm_polygons(fill = "FOREIGN_BORN", palette = "YlOrRd", n = 3)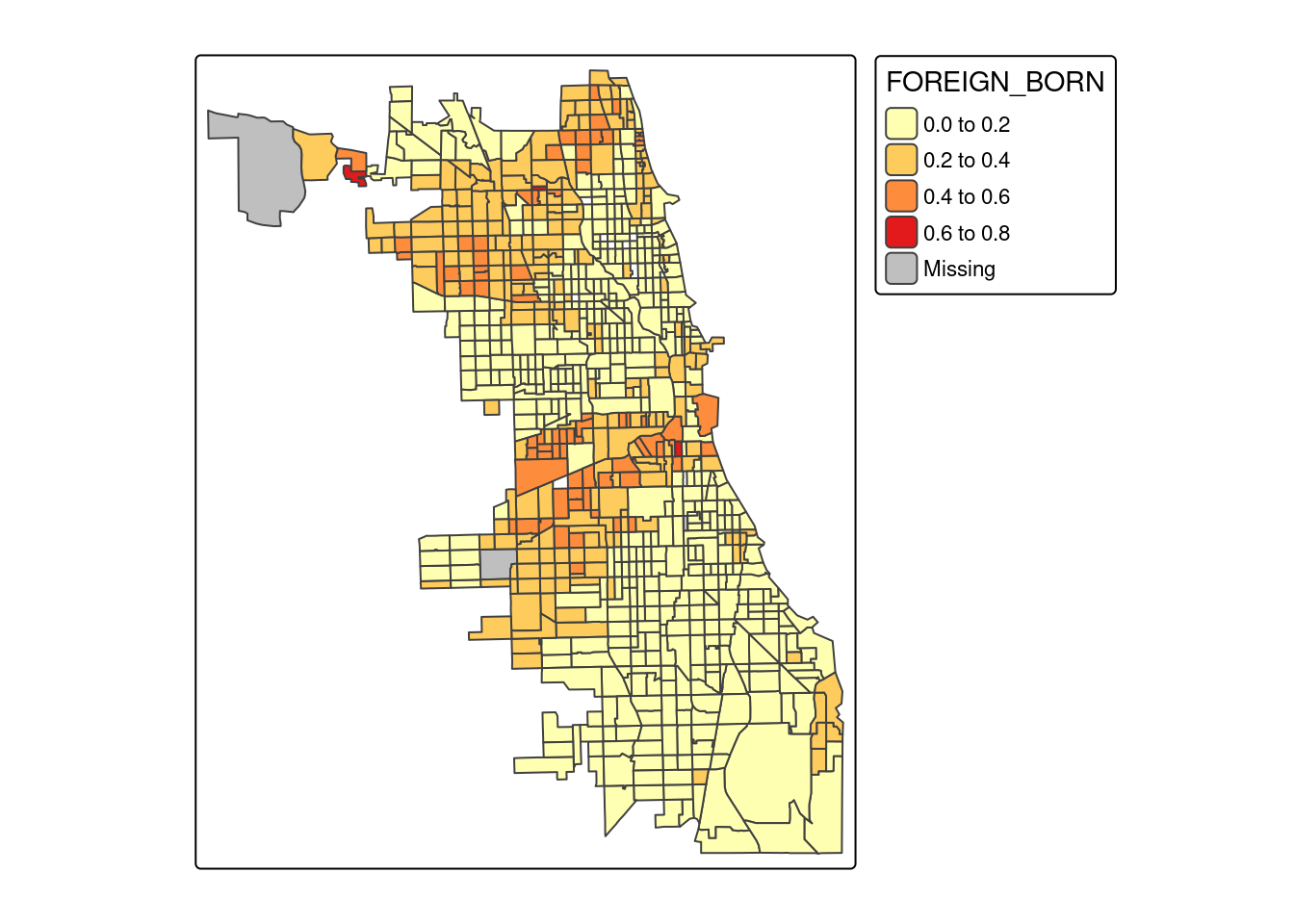

4.5.3 Poziom wykształcenia

tm_shape(socio_data) + 
  tm_polygons(fill = "EDU_HIGH", palette = "YlOrRd")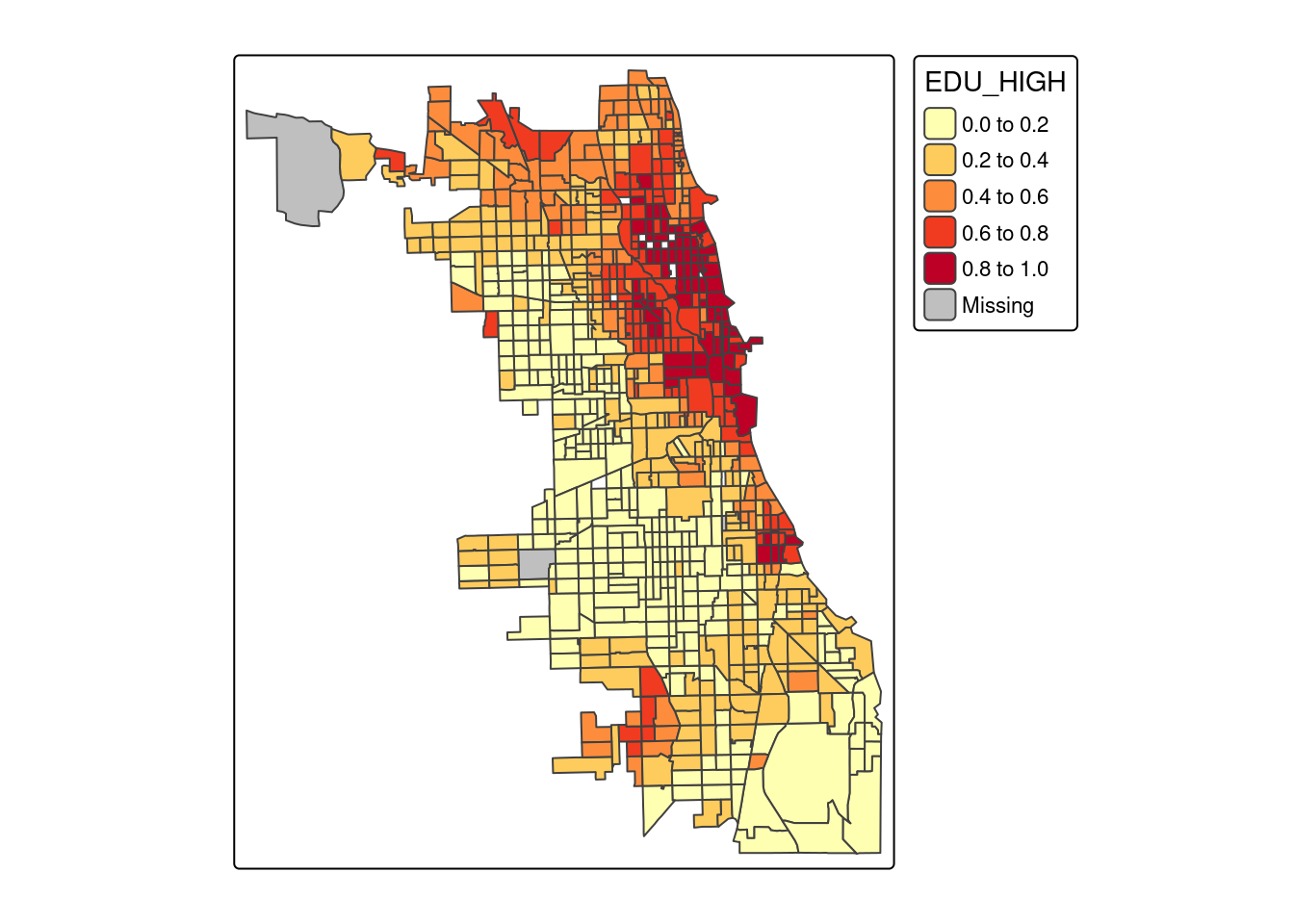

4.5.4 Zabudowa niezamieszkała

tm_shape(socio_data) + 
  tm_polygons(fill = "VACANT", palette = "YlOrRd")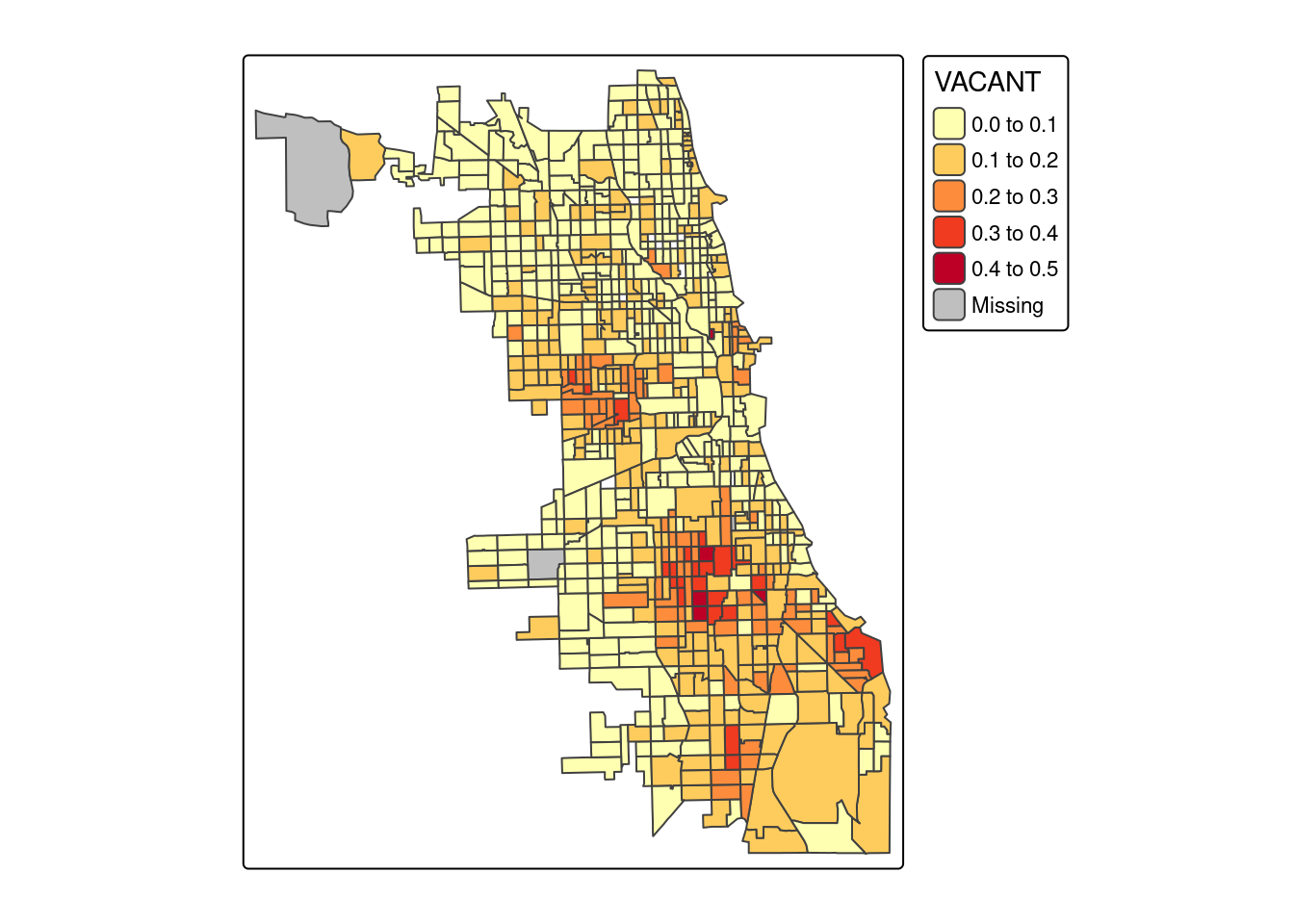

4.5.5 Poziom dochodów

tm_shape(socio_data) + 
  tm_polygons(fill = "INCOME_CAT", palette = c(low="#FFF68F", medium="#EEB422", high="#FF4040"))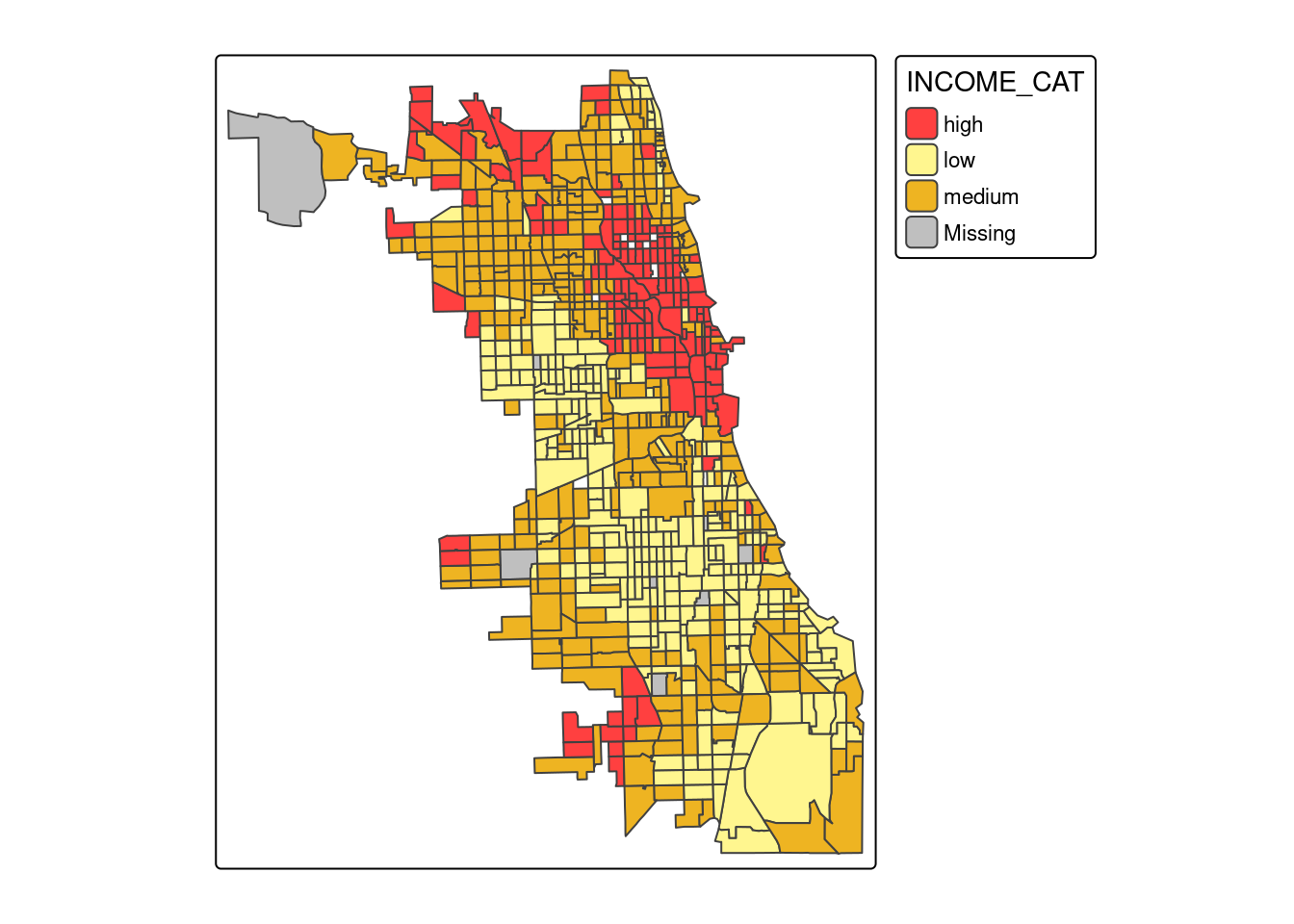

4.5.6 Ceny domów

tm_shape(socio_data) + 
  tm_polygons(fill = "HOME_VALUES_CAT", palette = c(low="#FFF68F", medium="#EEB422", high="#FF4040"))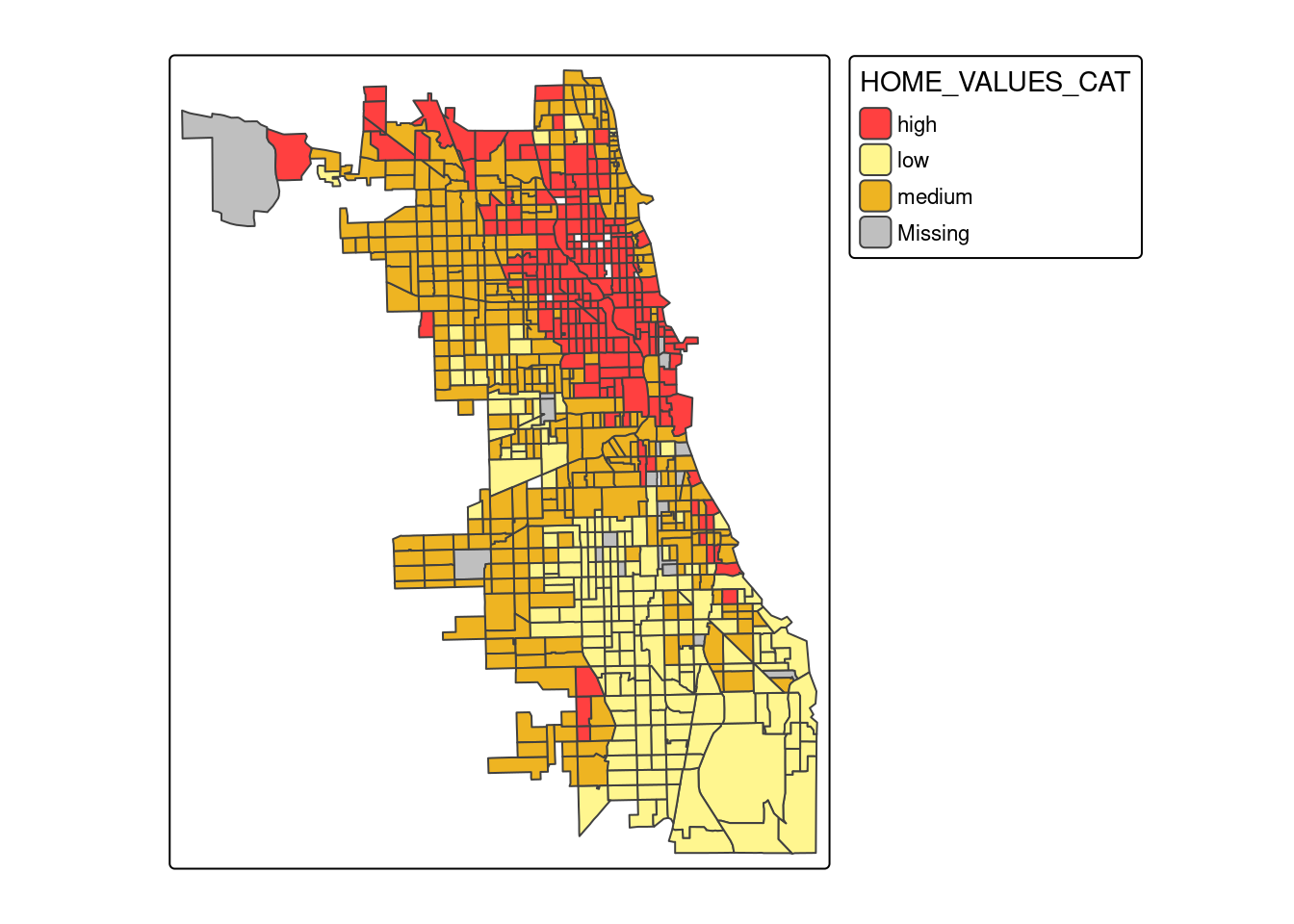

4.5.7 Wiek zabudowy

tm_shape(socio_data) + 
  tm_polygons(fill = "BUILT_YEAR_CAT", palette = c(old="#FFF68F", medium="#EEB422", new="#FF4040"))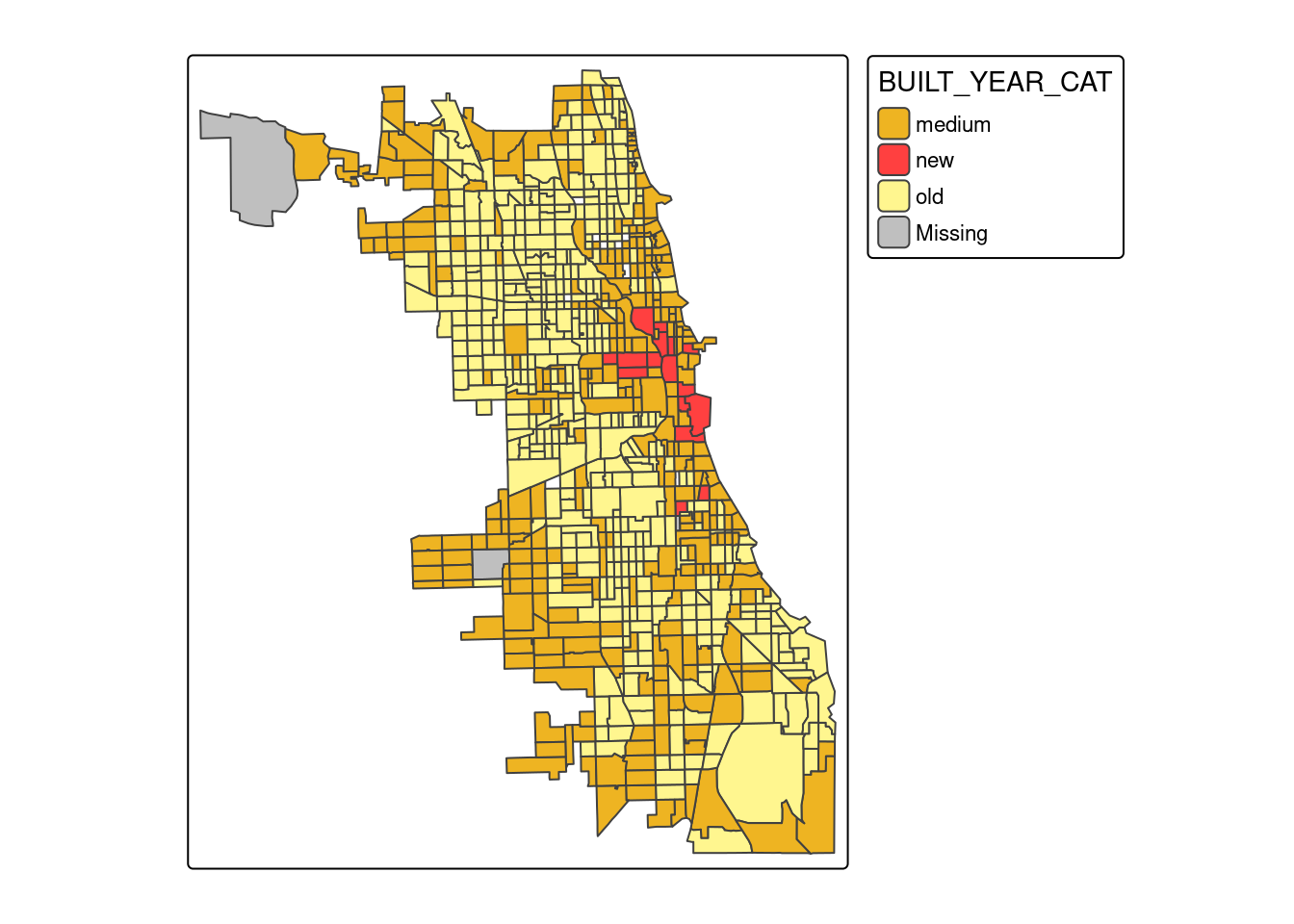

4.6 Podsumowanie

Przeprowadzona analiza korelacji wskazała na istnienie słabej zależności:
- wprostproporcjonalnej przekraczającej 0.5 między odsetkiem przestępstw na 1000 mieszkańców a odsetkiem czarnych (zmienna BLACK) oraz odsetkiem niezamieszkałej zabudowy (zmienna VACANT) oraz odsetkiem osób korzystających z pomocy społecznej
- odwrotnieproporcjonalnej przekraczającej 0.5 między odsetkiem przestępstw na 1000 miekszańców a odsetkiem ludności białej (zmienna WHITE), odsetkiem zamieszkałej zabudowy (zmienna OCCUPIED) oraz odsetkiem osób urodzonych za granicą.
Analiza wykresów pudełkowych pokazuje, że odsetek przestępczości przyjmuje wyższe wartości dla klasy o niskich dochodach, niskich cenach domów oraz dla obszarów o nowej zabudowie (powstałej po 2000 roku).
Obszary o niskim dochodzie (184 obszary), a także o małej wartości domów (258 obszarów) są zlokalizowane przede wszystkim w południowej części analizowanego obszaru.
Mapa przestępczości pokazuje wyższe wartości w południowej części analizowanego obszaru oraz środkowej części obszaru.