| Skala | Moda | Mediana | Średnia |
|---|---|---|---|
| Nominalna | X | ||
| Porządkowa | X | X | |
| Interwałowa | X | X | X |
| Ilorazowa | X? | X | X |
Statystyka opisowa
Statystyczne i graficzne podstawy geowizualizacji
Statystyka opisowa
Statystyka opisowa
jedna z podstawowych dziedzin statystyki, która zajmuje się zbieraniem, organizacją, analizowaniem oraz prezentacją danych statystycznych w celu opisania oraz podsumowania ich charakterystyk.
Cel:
- podsumowanie zbioru danych w sposób zrozumiały, przystępny i przejrzysty
- wyciągnięcie pewnych podstawowych wniosków i uogólnień na temat zbioru.
Statystykę opisową stosuje się zazwyczaj jako pierwszy i podstawowy krok w analizie zebranych danych.
Statystyka opisowa: zastosowania
- Eksploracja i organizacja danych
- zrozumienie struktury danych,
- wykrycie braków danych,
- wykrycie prostych błędów kodowania (np. rok urodzenia w bazie studentów: 99)
- wstępna ocena jakości danych
- Identyfikacja wzorców i tendencji
Źródło: https://pogotowiestatystyczne.pl/slowniki/statystyka-opisowa/
Statystyka opisowa: zastosowania
3. Tworzenie tabel dla zmiennych
zestawienie tabelaryczne statystyk pozwala w przejrzysty sposób ująć wszystkie najważniejsze informacje dotyczące danej analizy.
tabele sprawdzają się w przypadku potrzeby dokładnego raportowania wartości różnych statystyk.
nieczytelne w przypadku dużych zbiorów danych.
Źródło: https://pogotowiestatystyczne.pl/slowniki/statystyka-opisowa/
Statystyka opisowa: zastosowania
4. Wizualizacja danych
- alternatywa do tabelarycznego podsumowywania danych.
- pozwalają przyciągnąć uwagę czytelnika i zaprezentować informacje w prostszy sposób niżz złożone zestawienia tabelaryczne.
- wykresy najlepiej stosować dla naszych najciekawszych odkryć
Źródło: https://pogotowiestatystyczne.pl/slowniki/statystyka-opisowa/
Parametry statystyczne
Parametry statystyczne
Parametry statystyczne to liczby służące do syntetycznego opisu struktury zbiorowości statystycznej.

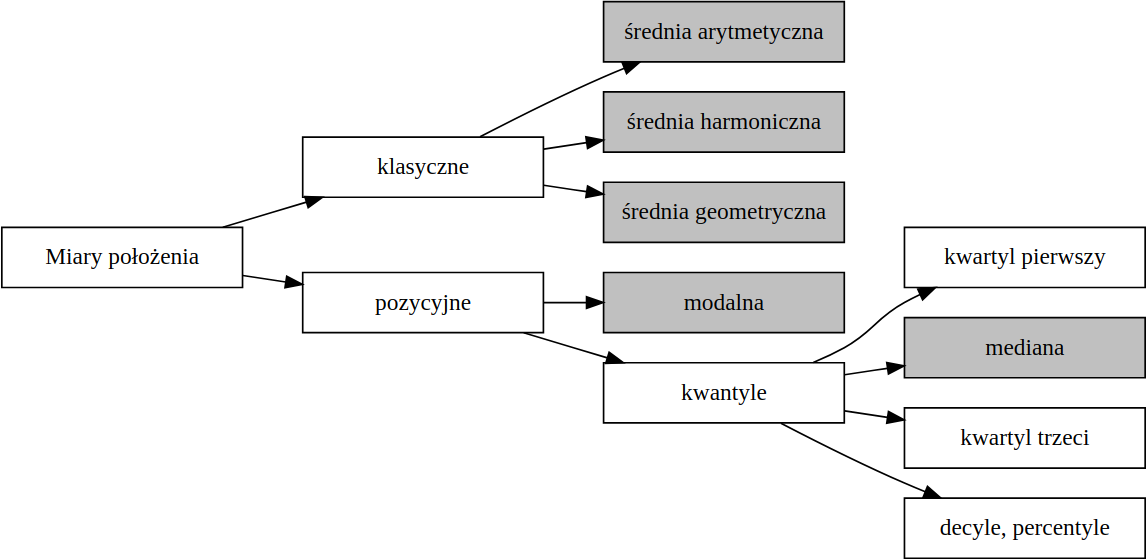
Miary położenia
Miary położenia określają przeciętny poziom wartości cecy statystycznej oraz umiejscowienie typowych wartości cechy statystycznej na osi liczbowej.
Miary klasyczne to miary, których wartość jest wyznaczona w oparciu o wszystkie obserwacje.
Miary pozycyjne to miary, na których wartość wpływają tylko wybrane obserwacje z próby uporządkowanej.

Miary położenia

Miary przeciętne/miary tendencji centralnej
Wśród miar położenia można wyróżnić miary przeciętne lub inaczej miary tendencji centralnej
- Średnie
- Wartość modalna
- Mediana
charakteryzują średni lub typowy poziom wartości zmiennej; mówią zatem o przeciętnym poziomie rozważanej zmiennej.
Miary położenia: średnie
| Średnia | Opis |
|---|---|
| Średnia arytmetyczna | najczęściej wykorzystywana miara położenia |
| Średnia harmoniczna | stosowana, gdy wartości cechy statystycznej podawane są w przeliczeniu na stałą jednostkę innej zmiennej, np. prędkość w km/h, gęstość zaludnienia w osobach/km2, spożycie w kg/osobę, itp. |
| Średnia geometryczna | stosowana gdy zjawiska są ujmowane dynamicznie, np. średnie tempo zmian; często odpowiednie dla wartości procentowych czy ułamkowych |
Dla każdego konkretnego przypadku powinno się obliczać tylko jedną średnią, bo tylko jedna z nich jest odpowiednia dla danej cechy statystycznej, a pozostałe nie mają sensu
Miary położenia: średnia arytmetyczna
- Najczęściej stosowana miara.
- Jej wadą jest wrażliwość na wartości odstające (ang. outliers)- tzn. pomiary, których wartość zdecydowanie odbiega od większości pozostałych.
- Obliczana na podstawie wszystkich obserwacji ze zbioru danych.
\[ \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i=\frac{x_1+x_2+\ldots+x_n}{n} \]
Miary położenia: średnia arytmetyczna
Trzy scenariusze, w których średnie wynagrodzenie w firmie zatrudniającej 10 osób wynosi 5000 zł.
Scenariusz 1
\[\bar{x}_A = \frac{10*5000}{10} = \frac{50000}{10} = 5000\] Scenariusz 2
\[\bar{x}_A = \frac{500 + 8*1500 + 37500}{10} = \frac{50000}{10} = 5000\] Scenariusz 3
\[\bar{x}_A = \frac{5*3000 + 5*7000}{10} = \frac{50000}{10} = 5000\] Źródło: Blog statystyczny https://statystyczny.pl/srednio-na-jeza-czyli-srednia-arytmetyczna/
Miary położenia: średnia harmoniczna
- obliczana jako odwrotność średniej arytmetycznej odwrotności wszystkich wartości z danego zbioru danych.
\[\bar{x}_H = \frac{n}{\sum\limits_{i=1}^n \frac1{x_i}} = \frac{n}{\frac1{x_1} + \frac1{x_2} + \cdots + \frac1{x_n}}\]
- Nie możliwa do wyliczenia na danych zawierających wartości ujemne lub zero.
Miary położenia: średnia harmoniczna
Przykład:
- Woda w rzece na pierwszym odcinku przepływa 100 kilometrów z prędkością 6 km/h, a na drugim odcinku 100 kilometrów z prędkością 3,2 km/h.
Jaka jest średnia prędkość wody w tej rzece?
Średnia arytmetyczna: 4.6 - błędny wynik
Średnia harmoniczna: 4.174
Sprawdzenie:
- przepłynięcie pierwszych 100 kilometrów z prędkością 6 km/h zabiera 16,667 godzin,
- przepłynięcie drugich 100 kilometrów z prędkością 3,2 km/h zabiera 31,25 godzin.
- W sumie jest to 47,917 godzin, co oznacza 200km/47,917 godzin, czyli 4,17 km/h.
Miary położenia: średnia geometryczna
- Średnia geometryczna n liczb, to pierwiastek n-tego stopnia z iloczynu tych liczb
- Nie możliwa do wyliczenia na danych zawierających wartości ujemne lub zero
\[\bar{x}_G = \sqrt[n]{\prod_{i=1}^n x_i} = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n}\]
Miary położenia: średnia geometryczna
Oczekiwana długość życia w Polsce (lata 1997, 2002, 2007): 72.75, 74.67, 75.563
- Zmiana pomiędzy 1997 a 2002:
\[x_1 = \frac{74.67}{72.75} = 1.026392 \]
- Zmiana pomiędzy 2002 a 2007:
\[x_1 = \frac{75.563}{74.67} = 1.011959 \]
- Średni przyrost (średnia geometryczna):
\[\bar{x}_G = \sqrt{1.026392 * 1.011959} = 1.01915\]
Miary położenia: średnia geometryczna
Gdyby w tym przykładzie zastosować średnią arytmetyczną uzyskalibyśmy wynik:
\[\frac{(1.026392 + 1.011959)}{2} = 1.019176\]
Wynikałoby z tego (błędnie), że w roku 2007 oczekiwana długość życia w Polsce powinna wynosić:
\[72.75 * 1.019176 * 1.019176 = 75.56686\]
W rzeczywistości ta wartość wynosiła:
\[72.75 * 1.01915 * 1.01915 = 75.563\]
Miary położenia: średnia ważona
- Wartości, którym przypisano wyższe wagi ( \(w\) ) mają większy udział w określeniu średniej ważonej niż dane, którym przypisano niższe wagi
\[ \bar{x}_w = \frac{w_1 x_1 + w_2 x_2 + \cdots + w_n x_n}{w_1 + w_2 + \cdots + w_n} \]
- Jeśli wszystkie wagi są równe, to wówczas średnia ważona jest równa średniej arytmetycznej.
- Wagi powinny być liczbami nieujemnymi.
- Można obliczać także inne średnie ważone, jak średnia ważona geometryczna i średnia ważona harmoniczna.
Miary położenia: miary pozycyjne
Miary pozycyjne to miary, na których wartość wpływają tylko wybrane obserwacje z próby uporządkowanej

Miary położenia: wartość modalna
Określana jako: wartość modalna, moda, dominanta, wartość najczęstsza
wartość cechy statystycznej, która w danym rozkładzie empirycznym występuje najczęściej
- wartość najczęściej występująca w zbiorze danych
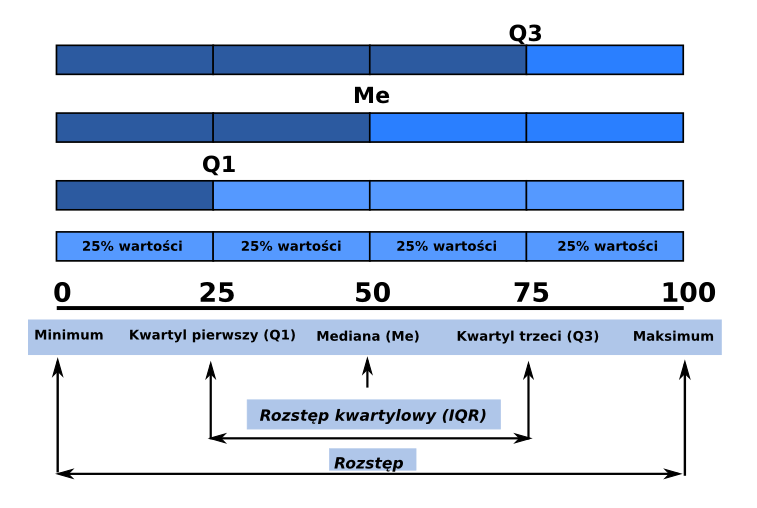
Miary położenia: kwantyle
Kwantyle to wartości cechy, które dzielą analizowany zbiór danych na określone części pod względem liczby jednostek. Części te pozostają w stosunku do siebie w określonych proporcjach:
Kwartyle - podział na 4 części:
- Kwartyl pierwszy (Q1)
- Mediana - kwartyl drugi
- Kwartyl trzeci (Q3)
Decyle - podzial na 10 części
Percentyle - podział na 100 częsci
Miary położenia: kwartyle
Kwartyle - podział na 4 części:
- Kwartyl pierwszy (Q1) - 25% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu, a 75% równe bądź wyższe
- Mediana (Me, kwartyl drugi) - połowa jednostek ma wartości cechy mniejsze bądź równe medianie, a połowa wartości cechy równe lub większe od Me
- Kwartyl trzeci (Q3) - 75% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi trzeciemu, a 25% równe bądź wyższe
Miary położenia: mediana
- Wartość środkowa
- Połowa wartości danych jest niższa, połowa jest wyższa
W przypadku nieparzystej liczby obserwacji mediana jest równa wartości środkowej:
- A: 12, 15, 16, 18, 21
- Mediana: 16
\[Me = X_{\frac{n+1}{2}}\]
Miary położenia: mediana
W przypadku parzystej liczby obserwacji nie ma jednej wartości środkowej i mediana jest obliczana z dwóch środkowych wartości:
- B: 12, 15, 15, 16, 18, 21
- Mediana: (15+16)/2 = 15.5
\[Me = \frac{1}{2} (x_{\lfloor n/2\rfloor} + x_{\lceil (n+1)/2\rceil})\]
Miary położenia: mediana
Mediana jest niezależna od wartości skrajnych
Medianę można stosować do zmiennych o charakterze porządkowym.
Medianę stosuje się bardzo często równolegle ze średnią arytmetyczną - warto zwracać uwagę na różnice między tymi dwoma wartościami i za każdym razem zastanowić się, z czego one wynikają.
Miary położenia: mediana
Trzy scenariusze, w których średnie wynagrodzenie w firmie zatrudniającej 10 osób wynosi 5000 zł. Jaka będzie wartość mediany?
Scenariusz 1: Każdy pracowik zarabia 5000 zł
Mediana: 5000 zł
Scenariusz 2: Jeden pracownik zarabia 500, 8 pracowików 1500 zł, i jeden 37500 zł
Zarobki: 500, 1500, 1500,1500,1500,1500,1500,1500,1500,37500
Mediana: (1500 + 1500)/2 = 1500 zł
Scenariusz 3: 5 pracowików zarabia 3000 zł i 5 pracowników zarabia 7000 zł
Zarobki: 3000, 3000, 3000, 3000, 3000, 7000, 7000, 7000, 7000, 7000
Mediana: (3000 + 7000)/2 = 5000 zł
Źródło: Blog statystyczny https://statystyczny.pl/srednio-na-jeza-czyli-srednia-arytmetyczna/
Możliwości stostowania miar położenia
Na przykład, obliczanie średniej arytmetycznej z ocen (skala porządkowa) jest statystycznie niepoprawne.
Miary zmienności
Miary zmienności (rozproszenia, dyspersji) opisują rozrzut wartości cechy statystycznej w populacji wokół wartości przeciętnej.
Charakteryzują one stopień zróżnicowania jednostek zbiorowości pod względem badanej cechy

Miary zmienności

Miary zmienności: wariancja
- Wariancja jest średnią arytmetyczną kwadratów odchyleń poszczególnych obserwacji od średniej arytmetycznej zbiorowości
\[\sigma^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \bar{x})^2 = \frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \ldots + (x_n - \bar{x})^2}{n}\]
- Wariancja nie jest wyrażona w jednostkach cechy, ale w jednostkach podniesionych do kwadratu, np. wariancja dla wzrostu może mieć jednostkę cm2
Miary zmienności: wariancja
Wariancja i odchylenie standardowe to wśród statystyk opisowych wyjątki - inne obliczenia wykonuje się w zależności od tego czy dysponujemy danymi z całej populacji, czy też tylko z próby.
W przypadku, gdy posiadamy tylko wartości próby należy użyć \(n - 1\) zamiast \(n\).
Wszystkie inne statystyki opisowe liczy się tak samo niezależnie czy dysponujemy danymi z całej populacji, czy też tylko z próby.
Miary zmienności: odchylenie standardowe
Określa, o ile średnio odchylają się wartości badanej cechy od średniej arytmetycznej.
Obok średniej jest jednym z najczęściej stosowanych parametrów statystycznych:
- jest obliczane ze wszystkich obserwacji w zbiorze danych
- im zbiór danych jest bardziej zróżnicowany tym większe odchylenie standardowe.
Małe odchylenie standardowe - wartości są blisko średniej.
Duże odchylenie standardowe - wartości są daleko od średniej.
Miary zmienności: odchylenie standardowe
- Obliczane jako pierwiastkek kwadratowy z wariancji
\[s = \sqrt{\sigma^2}\]
- Pozwala to na uzyskanie miary zmienności o jednostce zgodnej z mianem badanej cechy statystycznej
\[s = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \bar{x})^2} = \sqrt{\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \ldots + (x_n - \bar{x})^2}{n-1}}\]
Miary zmienności: odchylenie standardowe
Trzy scenariusze, w których średnie wynagrodzenie w firmie zatrudniającej 10 osób wynosi 5000 zł. Jaka będzie wartość odchylenia standardowego?
Scenariusz 1: Każdy pracowik zarabia 5000 zł
- Odchylenie standardowe: 0
Scenariusz 2: Jeden pracownik zarabia 500, 8 pracowików 1500 zł, i jeden 37500 zł
- Odchylenie standardowe: 11423.66 zł
Scenariusz 3: 5 pracowików zarabia 3000 zł i 5 pracowników zarabia 7000 zł
- Odchylenie standardowe: 2108.185 zł
Źródło: Blog statystyczny https://statystyczny.pl/srednio-na-jeza-czyli-srednia-arytmetyczna/
Miary zmienności: typowy obszar zmienności
Po obliczeniu odchylenia standardowego i średniej arytmetycznej, można również wyliczyć sobie tzw. typowy obszar zmienności:
\[\bar{x} - s < x_{typ} < \bar{x} + s\]
Miary zmienności: odchylenie standardowe

Powyższa relacja dotyczy tylko zmiennych o rozkładzie normalnym!
Miary zmienności: rozstęp
- Rozstęp lub zakres danych to najprostsza miara zmienności
- Jest to różnica między najwyższą i najniższą zaobserwowaną wartością cechy statystycznej
- Rozstęp jest podatny na wartości odstające
\[R = x_{max} - x_{min}\]
Miary zmienności: rozstęp kwartylowy
- Kwartyli można użyć również do wyznaczenia typowego obszaru zmienności (rozstępu kwartylowego) do którego należy 50% obserwacji
\[IQR = Q3 - Q1\]
Miary zmienności: odchylenie ćwiartkowe
Odchylenie standardowe jest najczęściej stosowane do opisania odchylenia wartości cechy od średniej arytmetycznej.
Natomiast odchylenie ćwiartkowe jest miarą zmienności najczęściej używaną w parze z medianą.
Odchylenie ćwiartkowe mierzy poziom zróżnicowania tylko części jednostek pozostałej po odrzuceniu 25% jednostek o wartościach najmniejszych i 25% jednostek o wartościach największych.
Odchylenie ćwiartkowe (Q) jest połową różnicy między trzecim, a pierwszym kwartylem.
\[Q = \frac{(Q_3 - Q_1)}{2}\]
Miary zmienności: współczynniki zmienności
- Współczynnik zmienności jest ilorazem bezwzględnej miary zmienności cechy i średniej wartości tej cechy.
- W konstrukcji współczynnika zmienności można użyć zarówno miar klasycznych, jak i pozycyjnych.
- Współczynnik zmienności stosuje się zwykle, gdy chcemy ocenić zróżnicowanie kilku zbiorowości pod względem tej samej cechy, ewentualnie tej samej zbiorowości pod względem kilku cech.
- Współczynnik zmienności jest wielkością niemianowaną. Wartości współczynników podaje się z reguły w procentach.
- Duże wartości współczynnika zmienności świadczą o zróżnicowaniu (niejednorodności zbiorowości).
Klasyczne współczynniki zmienności
Współczynnik zmienności odchylenia standardowego ( \(V_s\) ):
\[V_s = \frac{s}{\bar{x}}\] , gdy \(\bar{x} > 0\)
Pozycyjne współczynniki zmienności
Odchylenie ćwiartkowe
\[V_Q = \frac{Q}{Me}\]
, gdy \(Me > 0\)
oraz
\[V_{Q_1,Q_3}=\frac{Q_3-Q_1}{Q_3+Q_1}\]
Możliwości stostowania miar zmienności
| Skala | Rozstęp | Percentyle | Odchylenie.standardowe |
|---|---|---|---|
| Nominalna | |||
| Porządkowa | X | ||
| Interwałowa | X | X | X? |
| Ilorazowa | X | X | X |
Miary asymetrii i koncentracji

Relacja między średnią, medianą a modą

Miary asymetrii: współczynnik skośności
 Asymetrię rozkładu określa się za pomocą współczynnika skośności.
Asymetrię rozkładu określa się za pomocą współczynnika skośności.
- skośność = 0 - rozkład symetryczny
- skośność < 0 - rozkład asymetryczny lewostronnie (rozkład ma dłuższy lewy ogon)
- skośność > 0 - rozkład asymetryczny prawostronnie (rozkład ma dłuższy prawy ogon)
Miary koncentracji: kurtoza
Miary koncentracji opisują koncentrację wartości cechy wokół średniej. Jedną z miar koncentracji jest kurtoza.

K > 0 - Im wyższa kurtoza, tym bardziej wysmukła jest krzywa liczebności,a zatem większa koncentracja wokół średniej (leptokurtyczny).
K < 0 - rozkład bardziej spłaszczony niż rozkład normalny (platykurtyczny).
Podsumowanie
Miary położenia
Miary tendencji centralnej:
średnia arytmetyczna
mediana
moda
Kwartyle
Podsumowanie
Miary zmienności
rozstęp
odchylenie standardowe
współczynnik zmienności - iloraz bezwzględnej miary zmienności cechy (np. odchylenia standardowego) i średniej wartości tej cechy.
Miary asymetrii: współczynnik skośności
Miary koncentracji: kurtoza