library(tidycensus)
library(tidyverse)
library(sf)
library(corrr)
library(PerformanceAnalytics)Analiza geoinformacyjna w naukach społecznych
Ćwiczenie 5 i 6: Zastosowanie regresji wielokrotnej do modelowania cen nieruchomości
1 Cel analizy
Celem ćwiczenia jest określenie zależności między cenami nieruchomości, a zmiennymi społeczno-ekonomicznymi. W ramach ćwiczenia zostanie zbudowany model regresji przewidujący ceny nieruchomości na podstawie zmiennych pozyskanych ze spisów ludności.
W ćwiczeniu wykorzystano materiały pochodzące z ksiązki autorstwa Kyle Walker pt. “Analyzing US Census Data: Methods, Maps, and Models in R” (https://walker-data.com/census-r/). Szczegółowe informacje znandują się w Rozdziale 8.2.
Analiza zostanie przeprowadzona dla miasta Dallas, TX wykorzystując dane z 2020 roku.
2 Dane społeczno-ekonomiczne dla obszaru Stanów Zjednoczonych
W ćwiczeniu zostaną wykorzystane dane z obszaru Stanów Zjednoczonych na poziomie obszarów spisowych (ang. census tract) zebrane w ramach American Community Survey i udostępnione jako dane 5-letnie (ACS 5 year*).
2.1 American Community Survey
American Community Survey (ACS) to coroczny program badań demograficznych prowadzony przez US Census Bureau. Program ten gromadzi dane dotyczące struktury ludności, gospodarstw domowych oraz gospodarki mieszkaniowej. Dane te dotyczą m.in. rasowo-etnicznej struktury ludności, statusu obywatelstwa USA, poziomu wykształcenia, dochodów, znajomości języka, migracji, zatrudnienia oraz szerokiego zakresu związanego z nieruchomościami (np. wiek zabudowy, liczba osób na pokój, status własności nieruchomości itp.). Dane te są wykorzystywane przez wiele interesariuszy z sektora publicznego, prywatnego i organizacji non-profit do przydzielania środków, śledzenia zmian demograficznych, planowania na wypadek sytuacji kryzysowych i zdobywania wiedzy o społecznościach lokalnych.
2.1.1 Dane udostępniane przez ACS
dane jednoroczne (ACS 1-year) - dostępne dla obszarów o liczbie ludności co najmniej 65 000 osób. Dane te obejmują jedynie 26% hrabstw ze względu na próg liczby ludności. Wybrane dane roczne są udostępniane także dla obszarów o liczbie ludności przekraczającej 20 000.
dane 5-letnie (ACS 5-year) - dostępne na poziomie lokalnym (grupy bloków lub obszary spisowe). Dane te zbierane są w ciągu 5 lat. Np. dane z okresu 2018-2022 udostępnione będą w 2023 roku.
2.1.2 Pobieranie danych ACS
Dane ACS mogą zostać pobrane m.in ze strony projektu National Historical Geographic Information System (NHGIS, https://nhgs.org).
Dane te mogą być także pobrane bezpośrednio w R używając pakietu
tidycensus(https://walker-data.com/tidycensus/).
3 Wykorzystanie pakietu tidycensus do pobrania danych
Pakiet tidycensus umożliwia użytkownikom korzystanie z wybranych API umożliwiających dostęp do różnych zasobów danych US Census Bureau. Pakiet pobiera dane tabelaryczne w formie przygotowanej do pracy z tidyverse oraz opcjonalnie umożliwia połączenie danych tabelarycznych z danymi przestrzennymi (granicami jednostek).
3.1 Pozyskanie informacji o dostępnych danych
Funkcja load_variables() wyświetla tabelę z dostępnymi zmiennymi dla danego zbioru danych. W poniższym przykładzie zdefiniowano rok jako 2020 oraz zbiór danych (dataset) jako acs5 - 5-letnie dane ACS. Wyświetlone zostaną zatem dostępne zmienne dla okresu 2016-2020.
#pozyskanie informacji o dostępnych danych
v = load_variables(
year = 2020,
dataset = c("acs5"),
cache = FALSE
)W wyniku otrzmamy tabelę składającą się z 4 kolumn:
- name - kod tabeli oraz zmiennej
- label - opis zmiennej
- concept - nazwa tabeli, z której pobrano dane
- geography - najmniejsza jednostka agregacji, dla której dostępne są dane.
head(v)# A tibble: 6 × 4
name label concept geography
<chr> <chr> <chr> <chr>
1 B01001A_001 Estimate!!Total: SEX BY AGE (WHI… tract
2 B01001A_002 Estimate!!Total:!!Male: SEX BY AGE (WHI… tract
3 B01001A_003 Estimate!!Total:!!Male:!!Under 5 years SEX BY AGE (WHI… tract
4 B01001A_004 Estimate!!Total:!!Male:!!5 to 9 years SEX BY AGE (WHI… tract
5 B01001A_005 Estimate!!Total:!!Male:!!10 to 14 years SEX BY AGE (WHI… tract
6 B01001A_006 Estimate!!Total:!!Male:!!15 to 17 years SEX BY AGE (WHI… tract 3.2 Pobranie danych
Funkcja get_acs() pozwala na pobranie danych udostępnianych przez American Community Survey dla wybranego obszaru w Stanach Zjednoczonych. Dane mogą zostać pobrane dla wybranej tabeli, np. tabela przechowująca dane o rasowo-etnicznej strukturze ludności, lub dla wybranych zmiennych.
Argumenty funkcji get_acs():
- geography - poziom agregacji danych
- table - nazwa tabeli zawierającej dane. Po zdefiniowaniu tabeli zostaną pobrane wszystkie kolumny znajdujące się w tabeli. Można także użyć argumentu variables to zdefiniowania wybranych kolumn z danymi.
- state - kod FIPS stanu (liczbiowy lub literowy). Dla District Columbia kod FIPS dla stanu to “DC” lub 11.
- county - kod FIPS lub nazwa hrabstwa (np. 001 dla obszaru District of Columbia).
- geometry - TRUE oznacza, że zostaną pobrane dane geoprzestrzenne z tabelą atrybutów, FALSE oznacza, że zostaną pobrane wyłącznie dane atrybutowe (bez kolumny geometry pozwalającej na wykonanie map).
- year - rok dla danych jednorocznych lub ostatni rok dla danych 5 letnich.
- output - opcja wide oznacza, że każda zmienna jest w osobnej kolumnie a wiersz odpowiada danej jednostce spisowej, output=tidy (domyślny) - tzw. “długi” format danych.
3.2.1 Dane dla wybranej tabeli
W poniższym przykładzie zostaną pobrane dane na poziomie obszarów spisowych (tract) dla hrabstwa Dallas, TX dotyczące rasowo-etnicznej struktury ludności. Dane te są przechowywane w tabeli B03002 (Hispanic or Latino Origin by Race). Wynikiem będzie obiekt sf. Dane można także pobrac w formie tabelarycznej (argument geometry = FALSE)
#pobranie danych
race_acs <- get_acs(
geography = "tract",
table = c("B03002"),
state = "TX", #
county = "Dallas", #FIPS code lub nazwa
geometry = TRUE,
year = 2020,
output = "wide",
) Pobrany zbiór danych zawiera dwa rodzaje kolumn: oznaczone jako E lub M. Do analizy wykorzystuje się dane oznaczone jako E (etimates) - wartość zmiennych.
race_acs <- race_acs %>%
select(!ends_with("M")) %>%
rename_with(.fn = ~str_remove(.x, "E$")) 3.2.2 Dane dla wybranych zmiennych
Funkcja get_acs() pozwala także na pobranie danych dla wybranych zmiennych, np. pobranie danych dotyczących mediany dochodu w gospodarstwie domowym, ogólnej liczby ludności, oraz mediany wieku zabudowy.
head(var_acs)Simple feature collection with 6 features and 5 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: -96.8425 ymin: 32.79879 xmax: -96.72218 ymax: 32.84366
Geodetic CRS: NAD83
# A tibble: 6 × 6
GEOID NAM total_population median_year_built median_income
<chr> <chr> <dbl> <dbl> <dbl>
1 48113000100 Census Tract 1, … 3985 1974 127625
2 48113000201 Census Tract 2.0… 2809 1954 156000
3 48113000202 Census Tract 2.0… 3876 1950 123571
4 48113000300 Census Tract 3, … 4815 1980 86741
5 48113000401 Census Tract 4.0… 4645 2001 52347
6 48113000405 Census Tract 4.0… 2406 1987 41121
# ℹ 1 more variable: geometry <MULTIPOLYGON [°]>plot(var_acs["median_income"])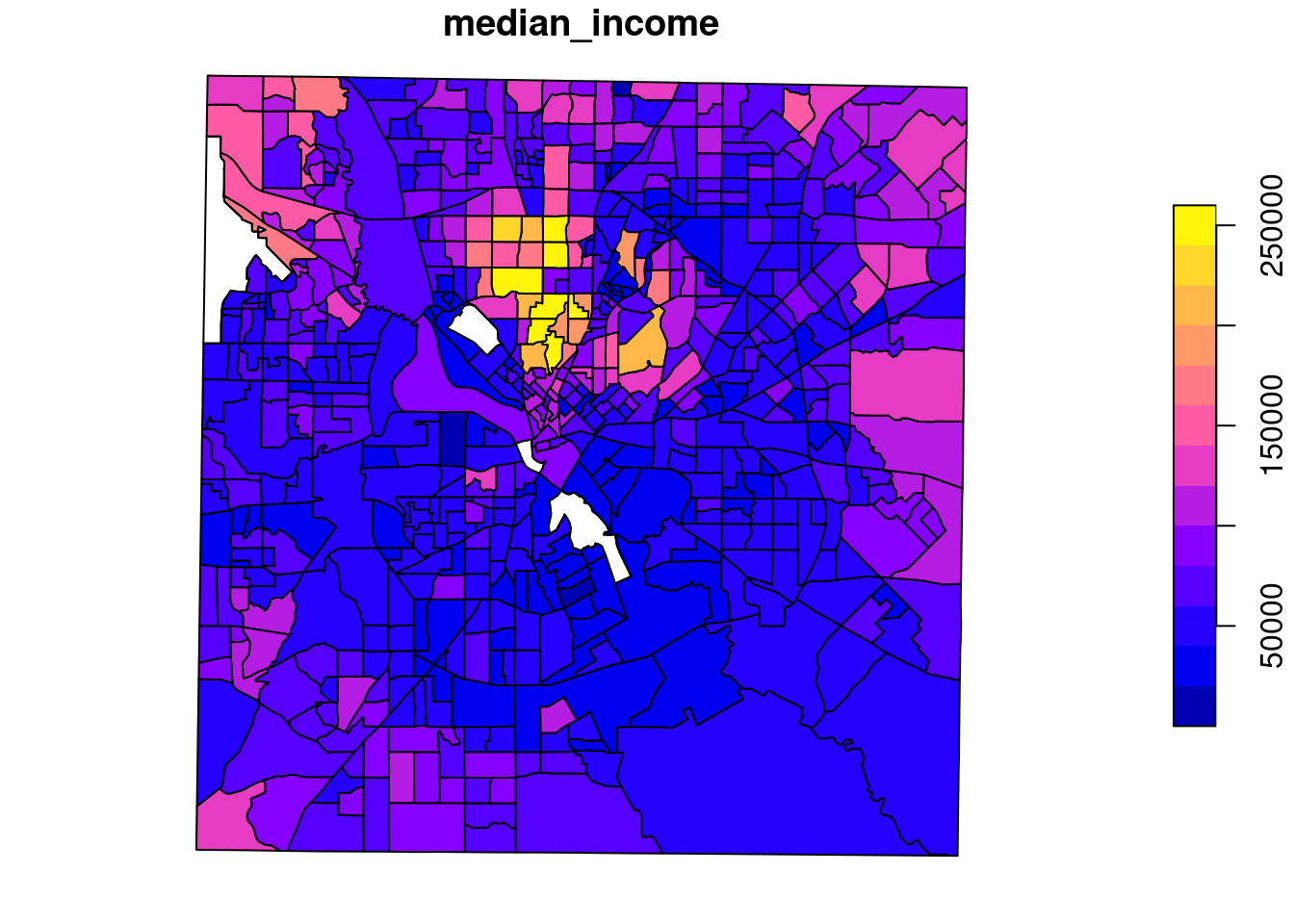
4 Przykład: Modelowanie cen nieruchomości w mieście Dallas, TX w 2020 roku.
4.1 Dane
Jako zmienną zależną w analizie regresji wykorzystano median_value - medianę wartości domów w obszarze spisowym.
W analizie uwzględnimy następujące zmienne niezależne pozyskane dla obszarów spisowych (ang. census tract):
- median_rooms: Mediana liczby pokoi w budynkach znajdujących się w obszarze spisowym;
- total_population: Ogólna liczba ludności w obszarze spisowym;
- median_age: Mediana wieku osób zamieszkujących dany obszar spisowy;
- median_year_built: Mediana wieku zabudowy znajdującej się w obszarze spisowym;
- median_income: Mediana dochodów w gospodarstwie domowym;
- pct_college: Procent ludności w wieku 25+ które ukończyły 4-letni college;
- pct_foreign_born: procent ludności urodzonej poza Stanami Zjednoczonymi;
- pct_white: procent ludności białej, nie mającej pochodzenia latynowskiego (non-Hispanic whites);
- percent_ooh: procent mieszkań zamieszkałych przez właścicieli.
4.2 Obszar analizy
Analiza zostanie przeprowadzona dla obszaru metropolitarnego Dallas, TX (Dallas metropolitan statistical area, w skrócie Dallas MSA). Obszar ten należy zdefiniować za pomocą hrabstw (ang. counties) wchodzących w skład Dallas MSA.
Hrabstwa wchodzące w skład Dallas MSA:
dfw_counties <- c("Collin County", "Dallas", "Denton",
"Ellis", "Hunt", "Kaufman", "Rockwall",
"Johnson", "Parker", "Tarrant", "Wise")4.3 Pobranie danych
Dane do analizy zostaną pobrane wykorzystując funkcję get_acs() z pakietu tidycensus().
Zmienne wykorzystane w analizie
variables_to_get <- c(
median_value = "B25077_001",
median_rooms = "B25018_001",
median_income = "DP03_0062",
total_population = "B01003_001",
median_age = "B01002_001",
pct_college = "DP02_0068P",
pct_foreign_born = "DP02_0094P",
pct_white = "DP05_0077P",
median_year_built = "B25037_001",
percent_ooh = "DP04_0046P"
)Pobranie danych
Z pobranych danych zostaną wybrane tylko kolumny oznaczone jako E - wartość zmiennej.
dfw_data <- dfw_data %>%
select(!ends_with("M")) %>%
rename_with(.fn = ~str_remove(.x, "E$")) 4.3.1 Obliczenie nowych zmiennych
4.4 Obliczenie nowych zmiennych
Poniższy kod tworzy dwie nowe zmienne: pop_density, która reprezentuje liczbę osób w każdym obszarze spisu ludności na kilometr kwadratowy, oraz median_structure_age, który reprezentuje średni wiek budynków mieszkalnych w obszarze (zmienna median_year_built wyraża rok budowy budynku)
library(sf)
library(units)udunits database from /usr/share/xml/udunits/udunits2.xmldfw_data <- dfw_data %>%
mutate(pop_density = as.numeric(set_units(total_population / st_area(.), "1/km2")),
median_structure_age = 2018 - median_year_built) library(sf)
write_sf(dfw_data, "dallas.gpkg")5 Eksploracyjna analiza danych
5.1 Statystyki opisowe
summary(dfw_data) GEOID median_value median_rooms total_population
Length:1704 Min. : 17700 Min. : 1.900 Min. : 0
Class :character 1st Qu.: 152800 1st Qu.: 4.725 1st Qu.: 3138
Mode :character Median : 222700 Median : 5.600 Median : 4306
Mean : 262620 Mean : 5.709 Mean : 4373
3rd Qu.: 324400 3rd Qu.: 6.600 3rd Qu.: 5385
Max. :2000001 Max. :10.000 Max. :12502
NA's :123 NA's :6
median_age median_year_built median_income pct_college
Min. :18.20 Min. : 0 Min. : 6935 Min. : 0.00
1st Qu.:31.25 1st Qu.:1974 1st Qu.: 52840 1st Qu.:17.40
Median :35.50 Median :1987 Median : 72453 Median :32.30
Mean :36.09 Mean :1944 Mean : 81558 Mean :36.02
3rd Qu.:40.20 3rd Qu.:1997 3rd Qu.:101272 3rd Qu.:52.50
Max. :81.10 Max. :2014 Max. :250001 Max. :92.40
NA's :5 NA's :23 NA's :12 NA's :5
pct_foreign_born pct_white percent_ooh geometry
Min. : 0.00 Min. : 0.00 Min. : 0.00 MULTIPOLYGON :1704
1st Qu.: 8.50 1st Qu.:22.60 1st Qu.: 42.12 epsg:5070 : 0
Median :16.20 Median :46.50 Median : 65.70 +proj=aea ...: 0
Mean :18.55 Mean :45.65 Mean : 60.07
3rd Qu.:26.70 3rd Qu.:67.35 3rd Qu.: 82.90
Max. :65.40 Max. :96.70 Max. :100.00
NA's :5 NA's :5 NA's :6
pop_density median_structure_age
Min. : 0.0 Min. : 4.00
1st Qu.: 664.8 1st Qu.: 21.00
Median : 1462.0 Median : 31.00
Mean : 1741.6 Mean : 73.52
3rd Qu.: 2303.5 3rd Qu.: 44.00
Max. :15445.6 Max. :2018.00
NA's :23 5.2 Analiza korelacji między zmiennymi
dfw_estimates <- dfw_data %>%
select(-GEOID, -median_value, -median_year_built) %>%
st_drop_geometry()library(PerformanceAnalytics)
chart.Correlation(dfw_estimates, histogram=TRUE, pch=19, method = "pearson")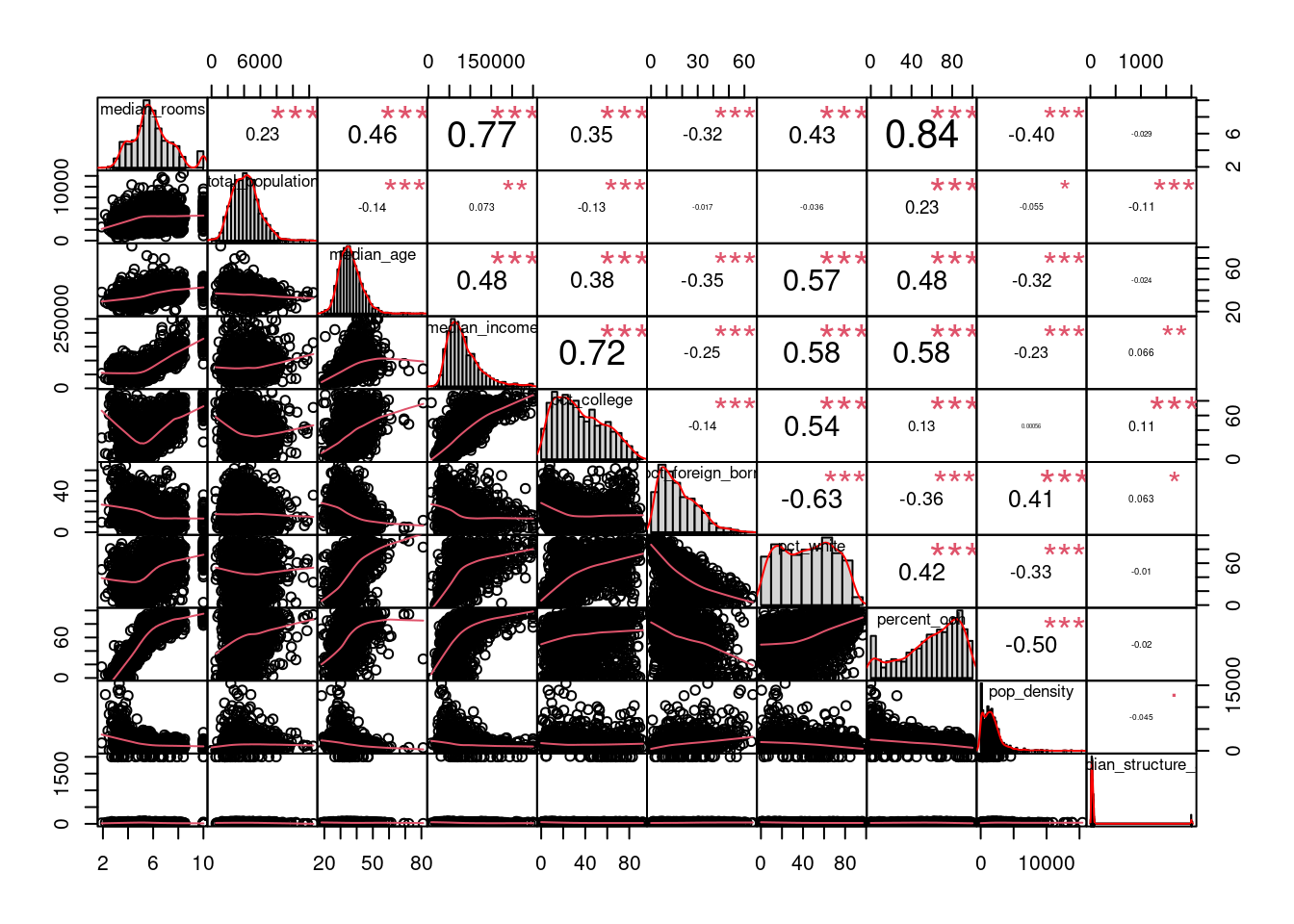
library("corrplot")corrplot 0.94 loadedlibrary("Hmisc")
Attaching package: 'Hmisc'The following objects are masked from 'package:dplyr':
src, summarizeThe following objects are masked from 'package:base':
format.pval, unitskor <- rcorr(as.matrix(dfw_estimates), type = "pearson")
corrplot.mixed(kor$r, order="hclust", tl.col="black")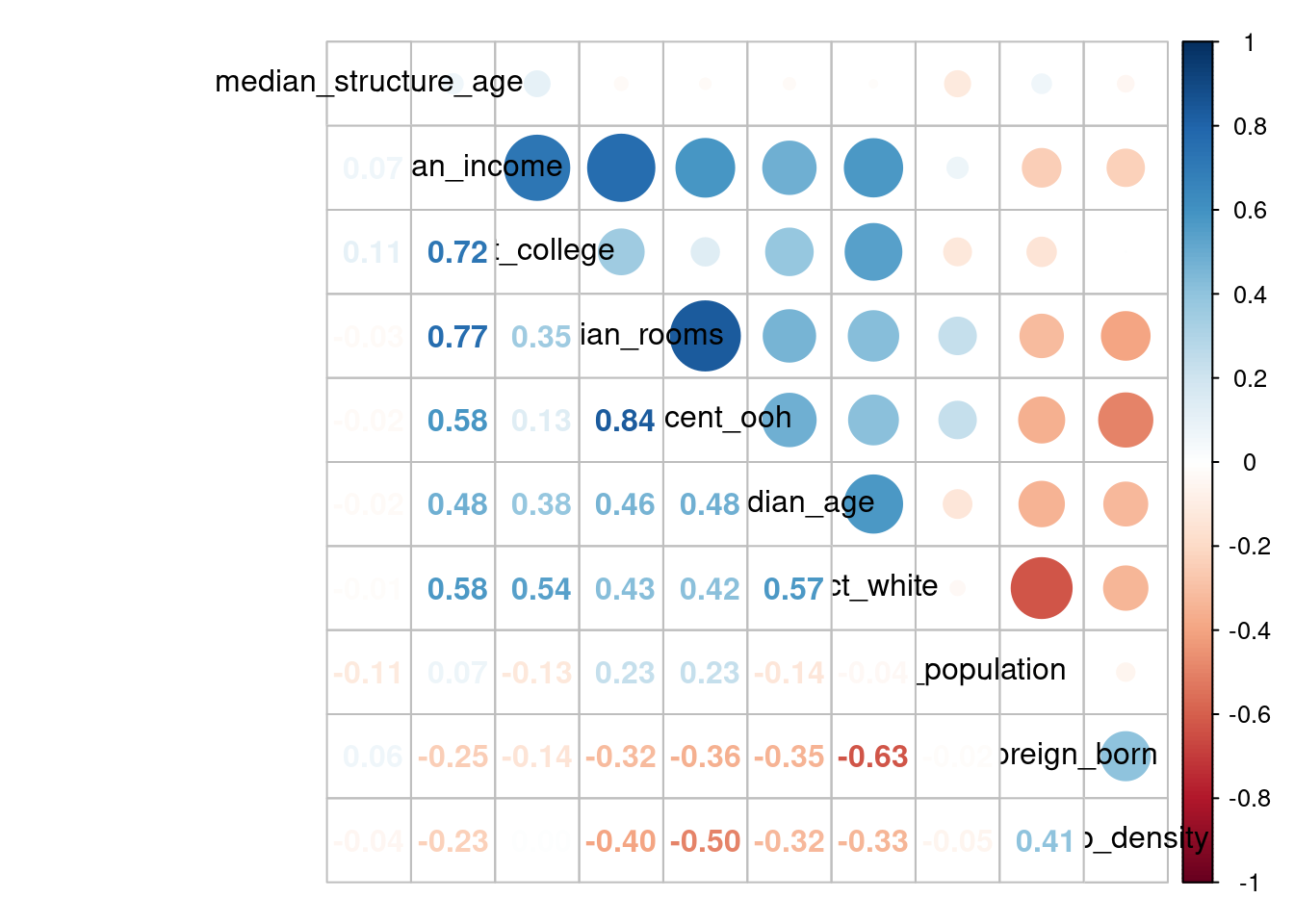
library(corrr)
correlations <- correlate(dfw_estimates, method = "pearson")Correlation computed with
• Method: 'pearson'
• Missing treated using: 'pairwise.complete.obs'network_plot(correlations)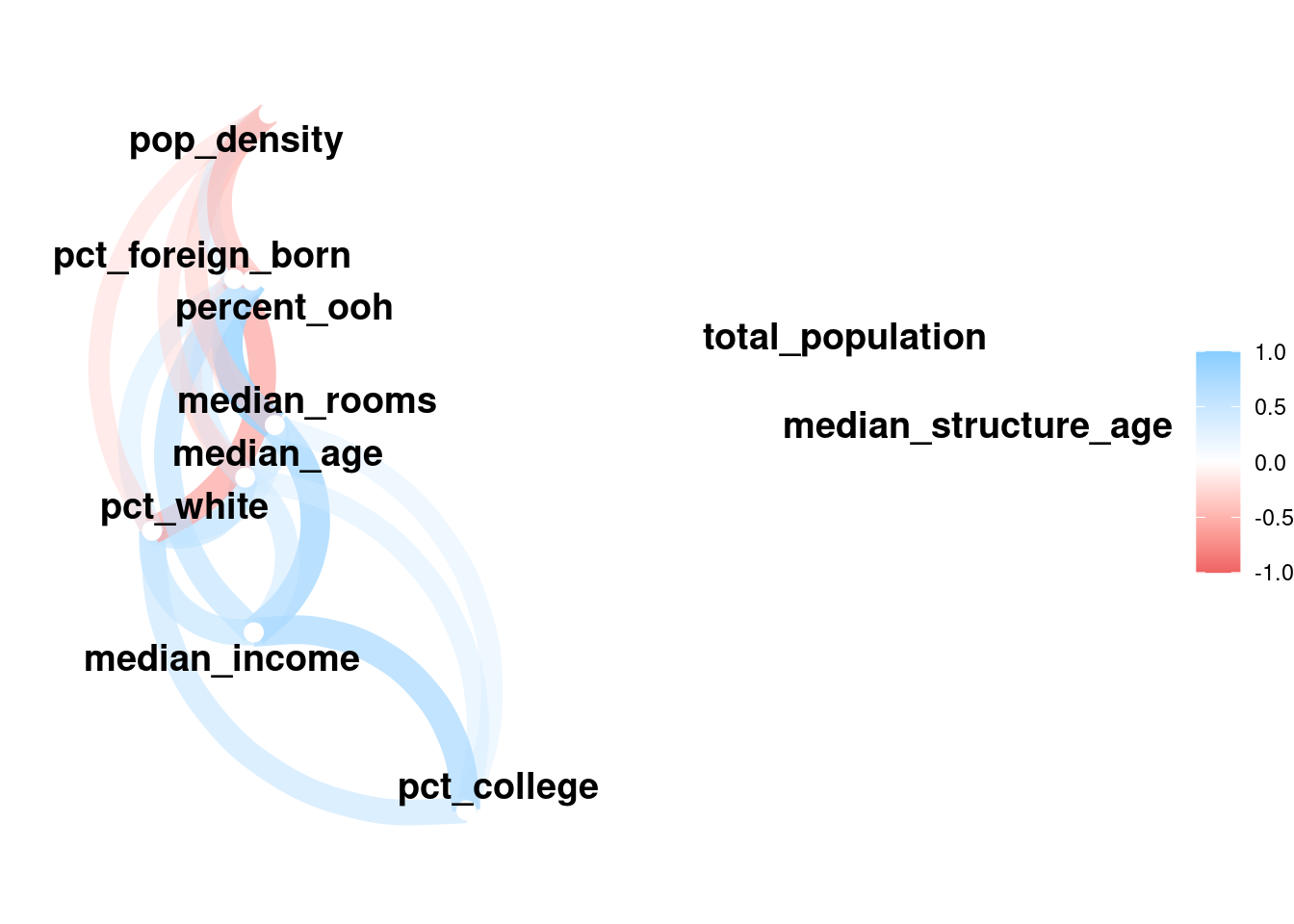
5.3 Przestrzenna eksploracja danych
5.3.1 Rozkład wartości cen nieruchomości
library(tidyverse)
library(patchwork)
mhv_map <- ggplot(dfw_data, aes(fill = median_value)) +
geom_sf(color = NA) +
scale_fill_viridis_c(labels = scales::label_dollar()) +
theme_void() +
labs(fill = "Median home value ")
mhv_histogram <- ggplot(dfw_data, aes(x = median_value)) +
geom_histogram(alpha = 0.5, fill = "navy", color = "navy",
bins = 100) +
theme_minimal() +
scale_x_continuous(labels = scales::label_number(accuracy = 0.1)) +
labs(x = "Median home value")
mhv_map + mhv_histogramWarning: Removed 123 rows containing non-finite outside the scale range
(`stat_bin()`).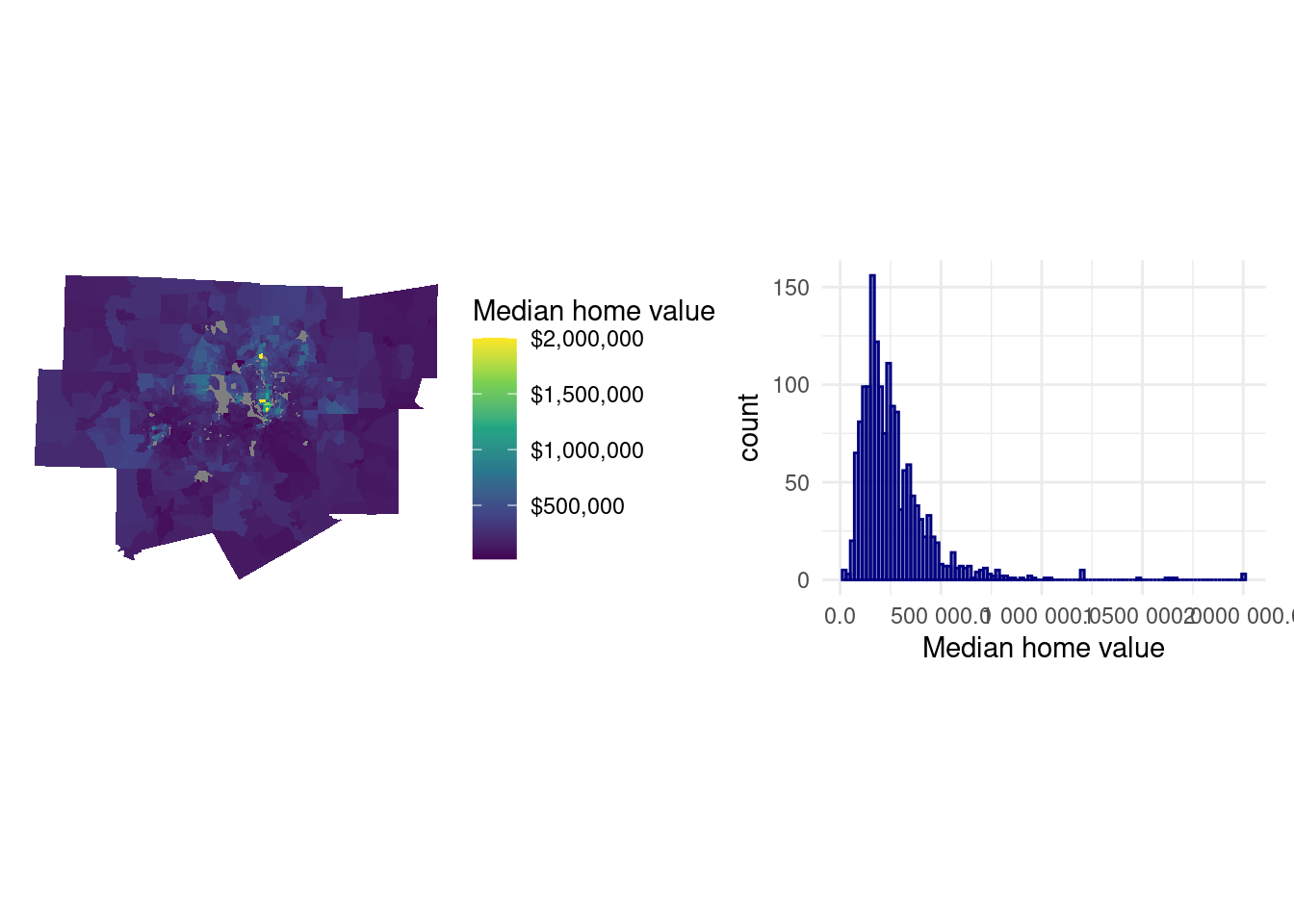
5.3.2 Mediana liczby pokoi
ggplot(dfw_data, aes(fill = median_rooms)) +
geom_sf(color = NA) +
labs(fill = "Median rooms") +
scale_fill_continuous(type = "viridis") +
theme_void() 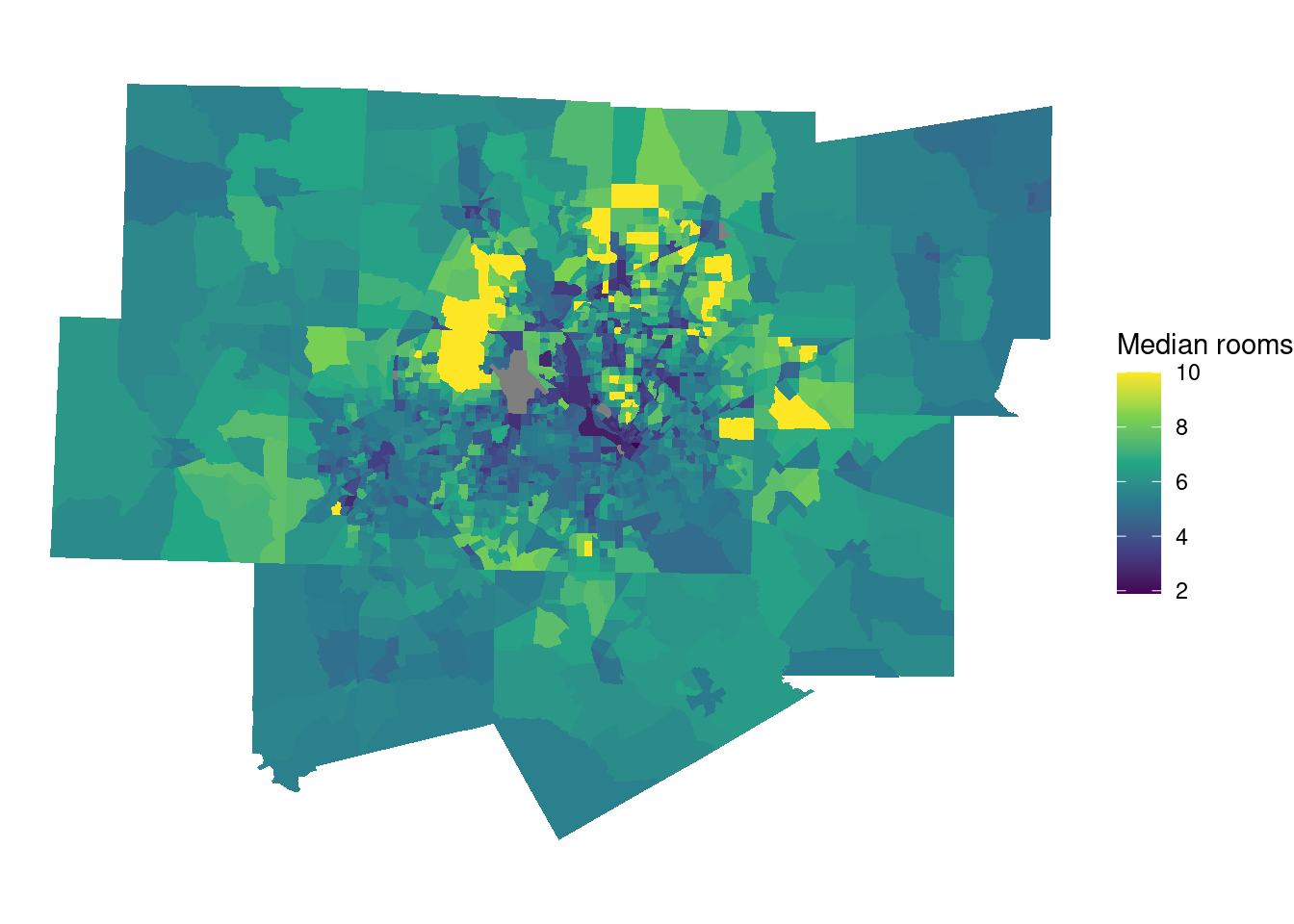
W ten sam sposób można zwizualizować pozostałe zmienne zależne.
6 Przygotowanie danych do analizy
6.1 Transformacja zmiennej zależnej
Wartość domów w obszarze metropolitarnym Dallas, TX wykazuje rozkład asymetryczny, prawostronny - z dużą liczbą obszarów spisowych o niskich cenach domów oraz długim ogonem bardzo drogich obszarów, zwykle zlokalizowanych na północ od centrum Dallas. Może to prowadzić do dalszych naruszeń normalności reszt modelu. Przed wykonaniem modelowania zmienna zależna zostanie przekształcona używając funkcji logarytmicznej. Taka operacja przybliży jej rozkład do normalnego i lepiej uchwyci geograficzne różnice w wartościach domów, które staramy się modelować.
library(tidyverse)
library(patchwork)
mhv_map_log <- ggplot(dfw_data, aes(fill = log(median_value))) +
geom_sf(color = NA) +
scale_fill_viridis_c() +
theme_void() +
labs(fill = "Median home\nvalue (log)")
mhv_histogram_log <- ggplot(dfw_data, aes(x = log(median_value))) +
geom_histogram(alpha = 0.5, fill = "navy", color = "navy",
bins = 100) +
theme_minimal() +
scale_x_continuous() +
labs(x = "Median home value (log)")
mhv_map_log + mhv_histogram_logWarning: Removed 123 rows containing non-finite outside the scale range
(`stat_bin()`).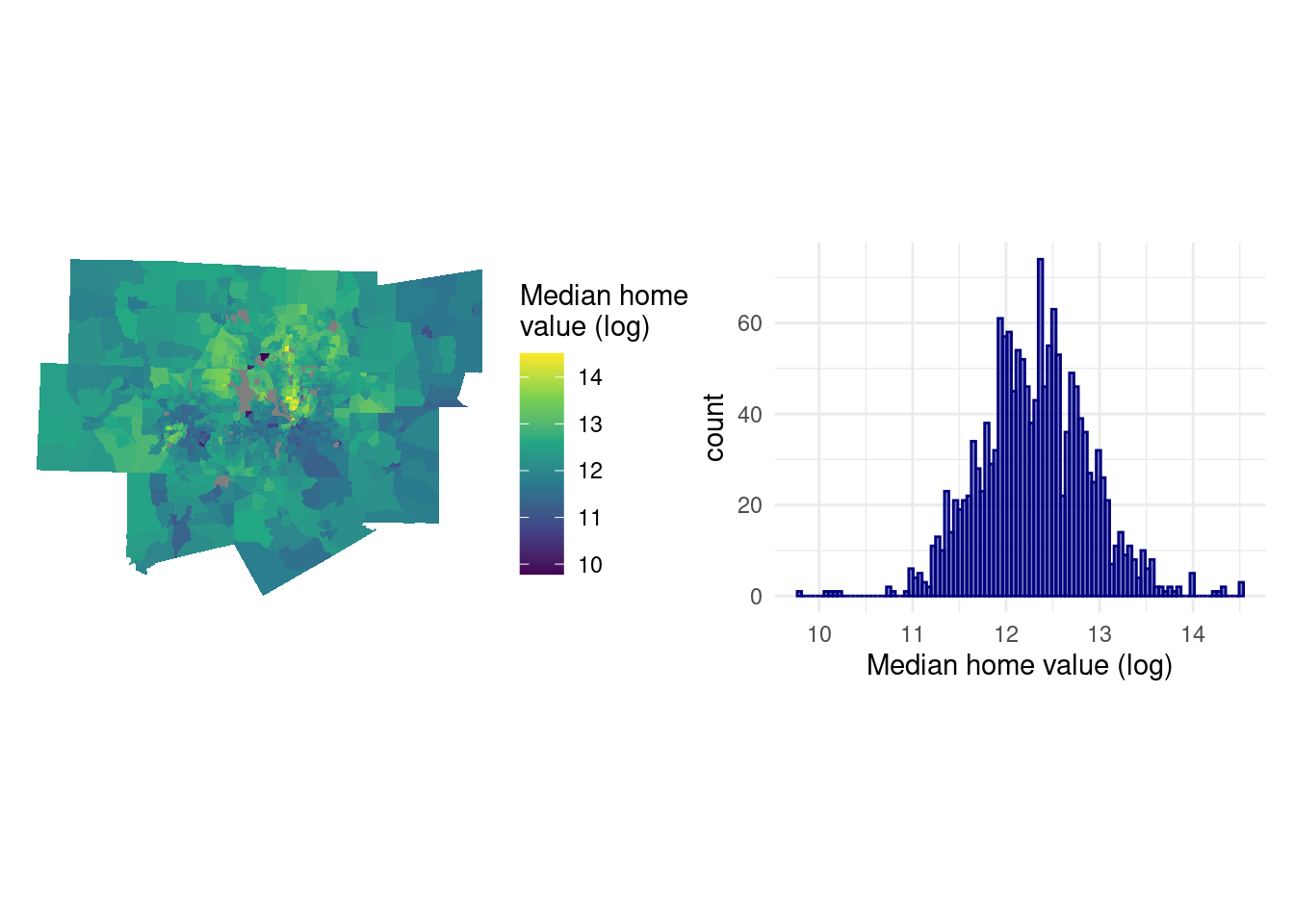
6.1.1 Dane do modelu
dfw_data_to_model <- dfw_data %>% na.omit()7 Budowa modelu regresji
formula <- "log(median_value) ~ median_rooms + median_income + pct_college + pct_foreign_born + pct_white + median_age + median_structure_age + percent_ooh + pop_density + total_population"
model1 <- lm(formula = formula, data = dfw_data_to_model)7.1 Wyniki modelu
summary(model1)
Call:
lm(formula = formula, data = dfw_data_to_model)
Residuals:
Min 1Q Median 3Q Max
-2.03016 -0.14248 0.00033 0.14793 1.45715
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.123e+01 6.199e-02 181.097 < 2e-16 ***
median_rooms 8.801e-03 1.058e-02 0.832 0.405632
median_income 5.007e-06 4.202e-07 11.915 < 2e-16 ***
pct_college 1.325e-02 5.993e-04 22.109 < 2e-16 ***
pct_foreign_born 2.877e-03 8.005e-04 3.594 0.000335 ***
pct_white 3.961e-03 4.735e-04 8.365 < 2e-16 ***
median_age 4.781e-03 1.372e-03 3.484 0.000507 ***
median_structure_age 1.201e-05 2.585e-05 0.465 0.642163
percent_ooh -4.761e-03 5.599e-04 -8.504 < 2e-16 ***
pop_density -7.947e-06 6.159e-06 -1.290 0.197117
total_population 8.961e-06 4.460e-06 2.009 0.044714 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2695 on 1548 degrees of freedom
Multiple R-squared: 0.7818, Adjusted R-squared: 0.7804
F-statistic: 554.6 on 10 and 1548 DF, p-value: < 2.2e-16Podsumowanie wyników modelu regresji składa się z kilku elementów:
- formuły użytej do budowy modelu (Call)
- statystyk reszt (Residuals) - reszty wyznacza się jako różnicę wartości obserwowanej oraz wartości oszacowanej z modelu.
- współczynników modelu (Coefficients)
- wyników mających na celu ocenę jakości uzyskanego modelu (Residual standard error, Multiple R-square, Adjusted R-squared)
Formuła użyta do budowania modelu
model1$calllm(formula = formula, data = dfw_data_to_model)Reszty z modelu
Do oceny poprawności dopasowania modelu wykorzystuje się reszty (tzw.residua). Reszty wyznacza się jako różnicę wartości obserwowanej Y a wartości oszacowanej z modelu Ŷ.
Statystyki reszt
- Min - minimum,
- 1Q - pierwszy kwartyl,
- Median - mediana,
- 3Q - trzeci kwartyl,
- Max - maksimum.
Interpretacja wyników:
- Duże odchylenia mediany od 0 mogą świadczyć o zależności nieliniowej.
- Średnia wartość błędu powinna być równa 0 - oznacza to, że błędy dodatnie i ujemne się równoważą
Współczynniki modelu
smr = summary(model1)
smr$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.122545e+01 6.198572e-02 181.0973810 0.000000e+00
median_rooms 8.801023e-03 1.058029e-02 0.8318319 4.056321e-01
median_income 5.006942e-06 4.202368e-07 11.9145716 2.232549e-31
pct_college 1.325070e-02 5.993462e-04 22.1085853 2.368145e-94
pct_foreign_born 2.877109e-03 8.004690e-04 3.5942793 3.354865e-04
pct_white 3.960900e-03 4.735204e-04 8.3647941 1.326320e-16
median_age 4.781347e-03 1.372231e-03 3.4843606 5.070647e-04
median_structure_age 1.201370e-05 2.584881e-05 0.4647679 6.421631e-01
percent_ooh -4.761327e-03 5.599163e-04 -8.5036402 4.263462e-17
pop_density -7.947271e-06 6.158939e-06 -1.2903635 1.971172e-01
total_population 8.960644e-06 4.460324e-06 2.0089672 4.471396e-02Tabela współczynniki zawiera następujące informacje dla każdego współczynnika:
- Estimate - oceny wartości współczynników równania regresji
- Std.Error - błąd standardowy współczynnika (wartość 1 odchylenia standardowego; dla rozkładu normalnego w przedziale średnia±1 odchylenie standardowe mieści się 66% wartości danych)
- t-value - wartość statystyki t
- p-value - poziom istotności dla współczynnika
Residual standard error (błąd standardowy reszt; standardowy błąd oceny)
- Wartość 1 odchylenia standardowego; dla rozkładu normalnego w przedziale średnia±1 odchylenie standardowe mieści się 66% wartości danych.
- Pokazuje o ile przeciętnie wartości empiryczne odchylają się od wartości teoretycznych (wynikających ze zbudowanego modelu)
Multiple R-Squared, Adjusted R-Squared
Przy ocenie dopasowania modelu należy zwrócić uwagę na wartość R2 przedstawiającą procent wariancji wyjaśnionej przez model, tzn. jaki procent zmienności zmiennej zależnej (objaśnianej) jest uwarunkowany zmiennością zmiennej niezależnej (objaśniającej).
Im wyższa wartość współczynnika R2 (maksymalnie to 1) tym lepsze dopasowanie modelu do danych.
Niestety również im więcej zmiennych w modelu tym wyższa jest wartość współczynnika R2. Aby uwzględnić liczbę zmiennych w modelu stosuje się modyfikację współczynnika R2, tzw. Zmodyfikowany R2 (ang. Adjusted R2)
p-value
- wartość poziomu istotności całego modelu
8 Budowa modelu - model 2.
W powyższym modelu nie wszystkie zmienne były istotne statystycznie. Analiza wyników korelacji pokazuje, że zmienna median_income jest mocno skorelowana z większością pozostałych zmiennych. Powtórzymy zatem budowę modelu bez uwzględnienia zmiennej median_income.
formula2 <- "log(median_value) ~ median_rooms + pct_college + pct_foreign_born + pct_white + median_age + median_structure_age + percent_ooh + pop_density + total_population"
model2 <- lm(formula = formula2, data = dfw_data_to_model)summary(model2)
Call:
lm(formula = formula2, data = dfw_data_to_model)
Residuals:
Min 1Q Median 3Q Max
-1.91753 -0.15319 -0.00222 0.16192 1.58950
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.101e+01 6.202e-02 177.570 < 2e-16 ***
median_rooms 7.326e-02 9.497e-03 7.714 2.18e-14 ***
pct_college 1.775e-02 4.862e-04 36.507 < 2e-16 ***
pct_foreign_born 4.170e-03 8.284e-04 5.034 5.38e-07 ***
pct_white 4.996e-03 4.862e-04 10.275 < 2e-16 ***
median_age 3.527e-03 1.429e-03 2.468 0.0137 *
median_structure_age 2.831e-05 2.696e-05 1.050 0.2939
percent_ooh -3.888e-03 5.798e-04 -6.705 2.81e-11 ***
pop_density -5.476e-06 6.429e-06 -0.852 0.3945
total_population 9.712e-06 4.658e-06 2.085 0.0372 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2815 on 1549 degrees of freedom
Multiple R-squared: 0.7618, Adjusted R-squared: 0.7604
F-statistic: 550.4 on 9 and 1549 DF, p-value: < 2.2e-169 Porównanie wyników modelu 1 oraz modelu 2.
summary(model1)
Call:
lm(formula = formula, data = dfw_data_to_model)
Residuals:
Min 1Q Median 3Q Max
-2.03016 -0.14248 0.00033 0.14793 1.45715
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.123e+01 6.199e-02 181.097 < 2e-16 ***
median_rooms 8.801e-03 1.058e-02 0.832 0.405632
median_income 5.007e-06 4.202e-07 11.915 < 2e-16 ***
pct_college 1.325e-02 5.993e-04 22.109 < 2e-16 ***
pct_foreign_born 2.877e-03 8.005e-04 3.594 0.000335 ***
pct_white 3.961e-03 4.735e-04 8.365 < 2e-16 ***
median_age 4.781e-03 1.372e-03 3.484 0.000507 ***
median_structure_age 1.201e-05 2.585e-05 0.465 0.642163
percent_ooh -4.761e-03 5.599e-04 -8.504 < 2e-16 ***
pop_density -7.947e-06 6.159e-06 -1.290 0.197117
total_population 8.961e-06 4.460e-06 2.009 0.044714 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2695 on 1548 degrees of freedom
Multiple R-squared: 0.7818, Adjusted R-squared: 0.7804
F-statistic: 554.6 on 10 and 1548 DF, p-value: < 2.2e-16summary(model2)
Call:
lm(formula = formula2, data = dfw_data_to_model)
Residuals:
Min 1Q Median 3Q Max
-1.91753 -0.15319 -0.00222 0.16192 1.58950
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.101e+01 6.202e-02 177.570 < 2e-16 ***
median_rooms 7.326e-02 9.497e-03 7.714 2.18e-14 ***
pct_college 1.775e-02 4.862e-04 36.507 < 2e-16 ***
pct_foreign_born 4.170e-03 8.284e-04 5.034 5.38e-07 ***
pct_white 4.996e-03 4.862e-04 10.275 < 2e-16 ***
median_age 3.527e-03 1.429e-03 2.468 0.0137 *
median_structure_age 2.831e-05 2.696e-05 1.050 0.2939
percent_ooh -3.888e-03 5.798e-04 -6.705 2.81e-11 ***
pop_density -5.476e-06 6.429e-06 -0.852 0.3945
total_population 9.712e-06 4.658e-06 2.085 0.0372 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2815 on 1549 degrees of freedom
Multiple R-squared: 0.7618, Adjusted R-squared: 0.7604
F-statistic: 550.4 on 9 and 1549 DF, p-value: < 2.2e-1610 Informacje zawarte w obiekcie klasy lm
Stworzenie ramki danych zawierającej wyniki modelu
#ramka danych zawierająca dane użyte do budowy modelu
model_df <- model2$model#reszty - różnica między warrtością obserwowaną Y a wartością oszacowaną z modelu Ŷ.
model_df$reszty <- model2$residuals#wartości oszacowane przez model
model_df$fitted <- model2$fitted.valueshead(model_df) log(median_value) median_rooms pct_college pct_foreign_born pct_white
1 12.12051 6.0 8.6 16.5 65.4
2 12.19854 6.0 19.2 20.0 68.8
3 12.68912 7.4 41.3 4.9 77.0
4 12.81284 7.3 40.9 8.3 72.5
5 12.28857 6.2 51.8 9.7 63.0
6 12.35104 6.3 31.7 28.3 45.9
median_age median_structure_age percent_ooh pop_density total_population
1 31.9 24 85.5 19.04821 2296
2 45.5 23 78.6 13.43260 2720
3 35.1 16 79.2 39.45031 3653
4 42.1 17 88.3 22.94960 3530
5 32.7 12 63.6 417.38793 6592
6 30.4 11 82.2 535.52724 5257
reszty fitted
1 0.31621693 11.80430
2 0.09561782 12.10293
3 0.14365946 12.54546
4 0.30188329 12.51096
5 -0.38396026 12.67253
6 0.12986691 12.2211710.1 Przestrzenna wizualizacja wyników modelu
#dołączenie pola GEOID
model_df$GEOID <- dfw_data_to_model$GEOID#dołączenie kolumny z geometrią
model_df <- full_join(dfw_data[, c("GEOID", "geometry")], model_df, by = "GEOID")library(colorspace)
ggplot(model_df, aes(fill = reszty)) +
geom_sf() +
scale_fill_continuous_diverging("Blue-Red 3") +
theme_void() 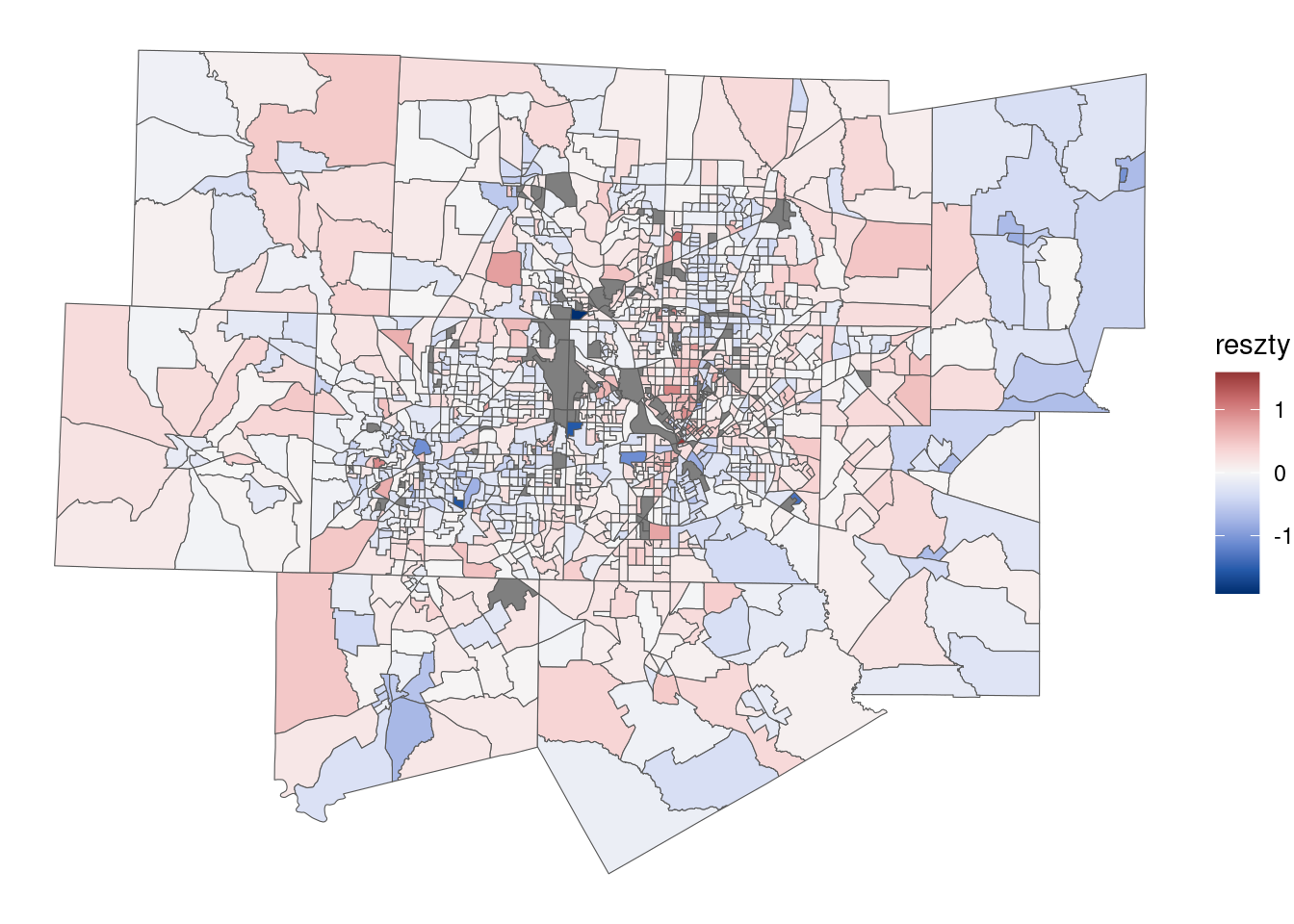
Reszty wyznacza się jako różnicę wartości obserwowanej Y a wartości oszacowanej z modelu Ŷ.
- Reszty dodatnie: wartość obserwowana jest większa od wartości oszacowanej przez model.
- Reszty ujemne: wartość obserwowana jest mniejsza od wartości oszacowanej przez model.